ネットワーク分析から直感的に理解するTransformerの仕組みと処理の流れ

昨今のDeepLearningの研究を席巻するTransformerの解説は複雑なものが多く、なかなか直感的に理解するのは難しいです。そこで当記事では「グラフ理論」や「ネットワーク分析」の知見を元に直感的にTransformerを理解できるように取りまとめを行いました。

概要

Transformerの解説などには難しいものが多いですが、基本的には下記に基づいて直感的に理解することができます。

① Transformerはネットワーク分析に類似する
② Transformerはグラフニューラルネットワークの一種である
③ グラフニューラルネットワークはRNNの拡張である

上記はどれも表立って解説されることが少ないので、解説コンテンツなどで取り扱われるケースは稀です。当記事では以下、必要な知識を前提知識で取り扱ったのちにTransformerの仕組みについて詳しく確認を行います。

前提知識

Word2vecに基づく単語のベクトル表記

単語をおよそ$100$〜$1,000$次元のベクトルに変換する手法の総称をWord$2$vecといいます。狭義にはWord$2$vecが$2013$年の研究を指す場合もありますが、単に「Word to Vector」の概念を表すと考えることもできるので当記事では総称と定めました。

Word$2$vecの大まかな理解にあたっては、「概念をベクトルで表す」ことが理解できれば良いです。たとえば新商品の紹介をする際に「レトルトカレー」であれば、「食品、保存食、温めが必要、辛い、肉入り」などに基づいて$0$or$1$の質的変数を作成することが可能です。

上記のように考えることで、「新商品のレトルトカレー」を属性を表す変数に基づくベクトルである程度表すことが可能になります。Word$2$vecは単語をベクトル化する手順ですが、レトルトカレーと同様にベクトル化を行うと大まかに理解しておけば当記事の理解にあたっては一旦十分です。

具体的な例があるとわかりやすいので、「本屋に行った。統計の教科書を買った。」を元に以下、Word$2$vecを適用する際の大まかな処理について確認します。

「本屋に行った。統計の教科書を買った。」という文を単語に分解し、動詞を基本形に直し助詞を除外すると「本屋、行く、統計、教科書、買う」のような単語の列が得られます。このような単語の列は数列を拡張して系列と表され、系列モデリングなどのようにいわれることも多いです。

ここでそれぞれの単語の意味に着目することで、単語を下記のようなベクトルの表記で表すことができます。

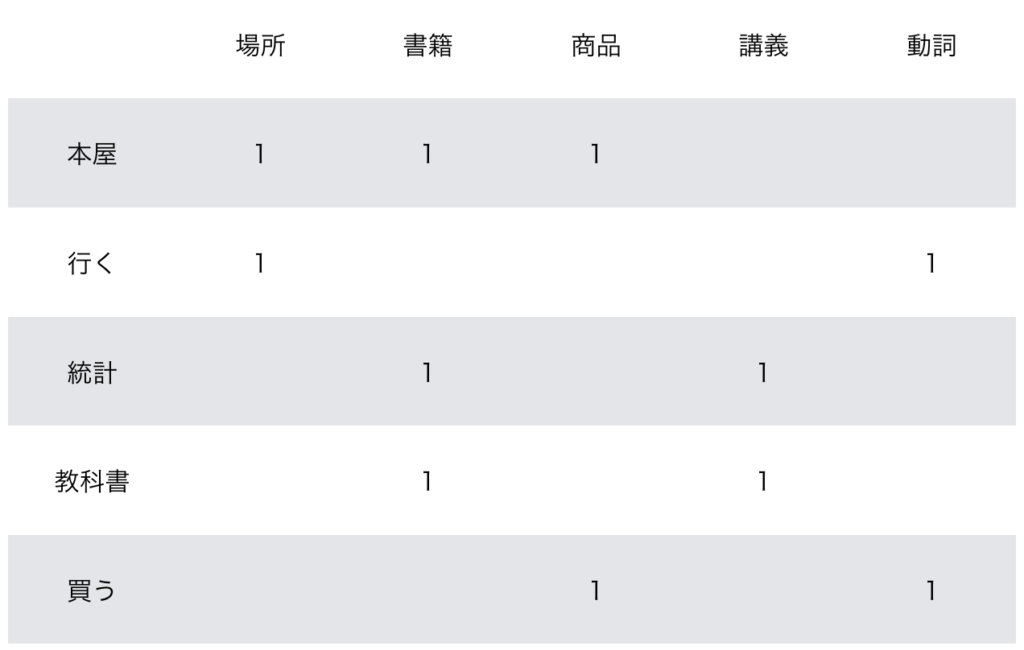
Word$2$vecを用いて単語をベクトルで表す際にベクトルの要素に具体的な意味を対応させるわけではありませんが、このように解釈することが可能であることは抑えておくと良いです。Word$2$vecの詳細に関しては「深層学習による自然言語処理」の$3$章の解説がわかりやすいのでここでは省略します。

グラフ理論と隣接行列

グラフ理論は点と線で物事を表す理論です。たとえば駅の路線図では下記のように駅を点、路線を線で表します。

上記の路線図では「駅と駅が隣接するかどうか」を中心に取り扱う一方で、それぞれの位置や方角などは厳密に再現はされません。このように、「隣接するかどうか」のみに着目して物事を表す際の理論を「グラフ理論」といいます。

グラフ理論では点をノード(node)、線をエッジ(edge)、全体をグラフ(graph)と定義します。数式で表すと$G = (V,E)$のように表しますが、$V$が頂点のVertice、$E$がEdge、$G$がGraphであるとそれぞれ解釈すると良いです。

グラフの表記法に関しては主に$2$通りあり、「①図を用いる」と「②隣接行列を用いる」をそれぞれ抑えておくと良いです。例があるとわかりやすいので下記のWikipediaの例を元に確認します。

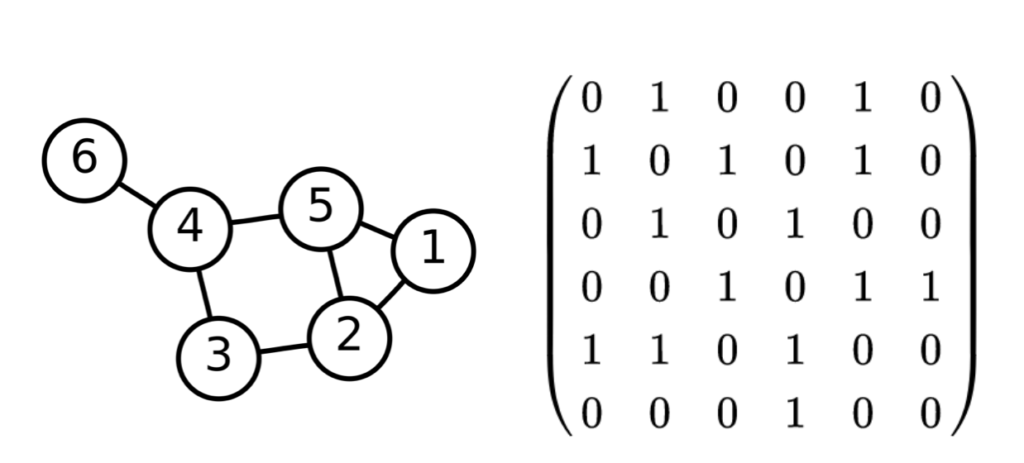
上記の例ではノードをそれぞれ行列の行と列に対応させ、$2$つのノードが連結する場合は$1$、連結しない場合は$0$をそれぞれの要素に持ちます。たとえば$1$と$2$が連結するので$1$行$2$列と$2$行$1$列が$1$であることが確認できます。

このようにグラフ理論ではノードとエッジを用いて概念を表す理論であり、グラフの表記法には「①図を用いる」と「②隣接行列を用いる」の$2$通りあることを大まかに理解しておけば当記事の範囲では十分です。

ネットワーク分析

グラフ理論の教科書などでは、特定の定義されたグラフについて取り扱うことが多いですが、言語の取り扱いを考える際は前々項で取り扱ったWord$2$vecのように何らかの手法に基づいて各単語にベクトルを割り当て、その類似度に基づいてグラフを作成することがよく行われます。

単語の類似度などに基づいてグラフを作成することを従来的には「ネットワーク分析」といいますが、この際によく用いられるのがcos類似度です。
$$
\large
\begin{align}
\cos{\theta} &= \frac{\vec{x} \cdot \vec{y}}{|\vec{x}||\vec{y}|} \\
-1 \leq & \cos{\theta} \leq 1
\end{align}
$$

$2$つのベクトル$\vec{x}, \vec{y}$のなす角を$\theta$とおくとき、内積$\vec{x} \cdot \vec{y}$を用いることで$\cos{\theta}$は上記のように計算することができます。内積の計算の詳細については当記事では省略しますので詳しくは下記をご確認ください。

統計学を学ぶにあたって最低限抑えておきたい数学　〜ベクトルの基本と内積〜

ここで$\cos{\theta}$は$2$つのベクトル$\vec{x}, \vec{y}$が同じ向きを向くかどうかの指標であると考えることができるので、ベクトルで表された単語の類似度を考えるにあたってcos類似度を用いるのは自然な考え方です。

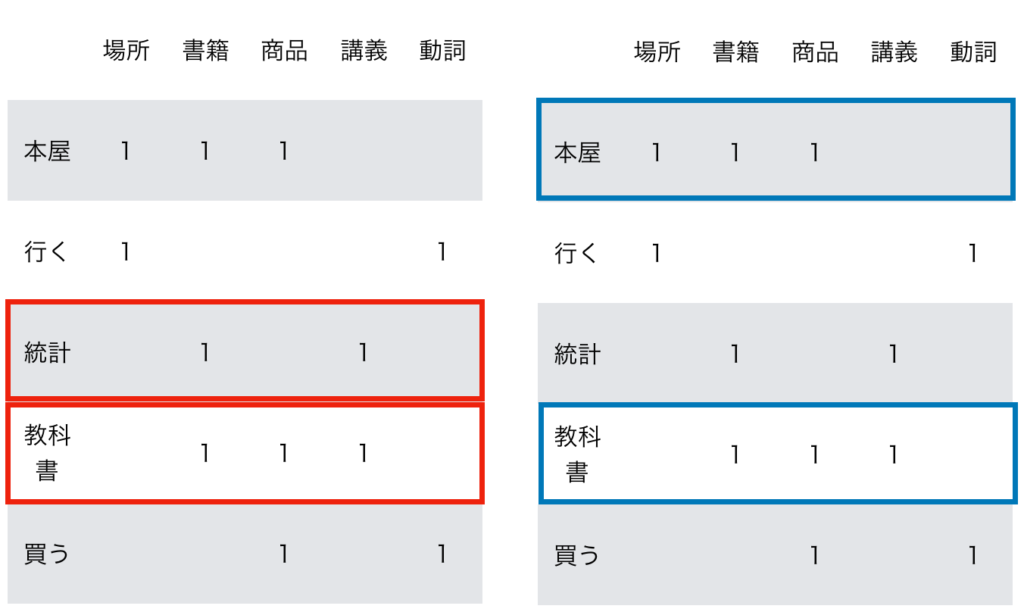
上図で表した表はWord$2$vecの概要を確認するにあたって用いましたが、それぞれ「統計と教科書」、「本屋と教科書」が類似したベクトルであることが確認できます。それぞれのcos類似度は下記のように計算できます。
・統計と教科書
$$
\large
\begin{align}
\vec{x} &= \left(\begin{array}{c} 0 \\ 1 \\ 0 \\ 1 \\ 0 \end{array} \right), \, \vec{y} = \left(\begin{array}{c} 0 \\ 1 \\ 1 \\ 1 \\ 0 \end{array} \right) \\
\cos{\theta} &= \frac{\vec{x} \cdot \vec{y}}{|\vec{x}||\vec{y}|} \\
&= \frac{2}{\sqrt{2} \times \sqrt{3}} = 0.816 \cdots
\end{align}
$$

・本屋と教科書
$$
\large
\begin{align}
\vec{x} &= \left(\begin{array}{c} 1 \\ 1 \\ 1 \\ 0 \\ 0 \end{array} \right), \, \vec{y} = \left(\begin{array}{c} 0 \\ 1 \\ 1 \\ 1 \\ 0 \end{array} \right) \\
\cos{\theta} &= \frac{\vec{x} \cdot \vec{y}}{|\vec{x}||\vec{y}|} \\
&= \frac{2}{\sqrt{3} \times \sqrt{3}} = 0.666 \cdots
\end{align}
$$

「ネットワーク分析」ではcos類似度などを用いて計算を行なった結果を元に閾値を設定することでエッジを描くかを判断します。上記の例では閾値を$0.55$に設定し、単語をノードで表し、類似する単語をエッジでつなげることで下記のようなグラフを描くことができます。

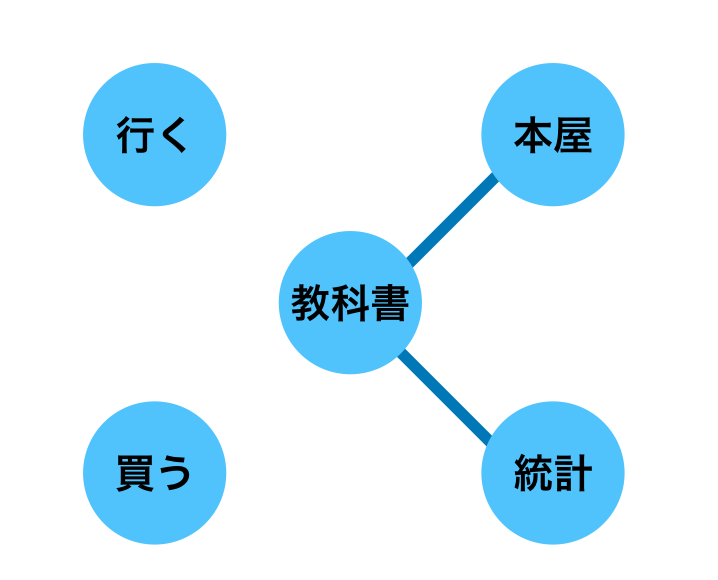
上記では閾値を$0.55$に設定したのでこのようなグラフとなったことに注意が必要です。たとえば閾値を$0.5$に変更すると、「行くと買う」のcos類似度が$0.5$であるので下記のようなグラフが得られます。

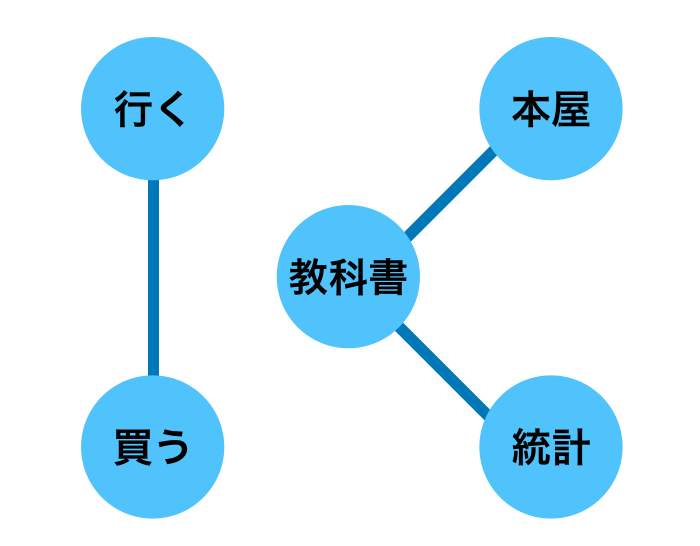
Transformerではネットワーク分析と同様の考え方を用いることは次節で確認します。DeepLearning以前のネットワーク分析では単語の共起に基づくBag of Wordsなどが用いられましたが、TransformerではWord$2$vecが用いられるので当項ではWord$2$vecを元に確認を行いました。

数列・系列・言語モデル

「数列」を数以外の記号などを取り扱えるように拡張したものを「系列」といいます。「系列」はよく出てくるので、数列と対応させて理解しておくと良いと思います。言語モデルは当記事では省略しますが、「深層学習による自然言語処理」の$3$章が詳しいのでこちらなど参照ください。

DeepLearningとMLP

DeepLearningにおけるMLPは多層パーセプトロン(Multi Layer Perceptron)を意味しますが、グラフニューラルネットワークの一種であるTransformerではMLPの計算が途中で用いられます。MLPの解説などは「ゼロから作るDeepLearning」など、わかりやすいものが多いので、当記事では省略します。

LSTMの限界とAttention

LSTMはRNNを改良したニューラルネットワークであり、長い系列に対応できるとされますが、$20$〜$50$系列ほどが上限であり、それ以上の取り扱いが難しいです。そこで横に展開するRNNの層の重み付け和を取るAttentionという構造が考案されました。

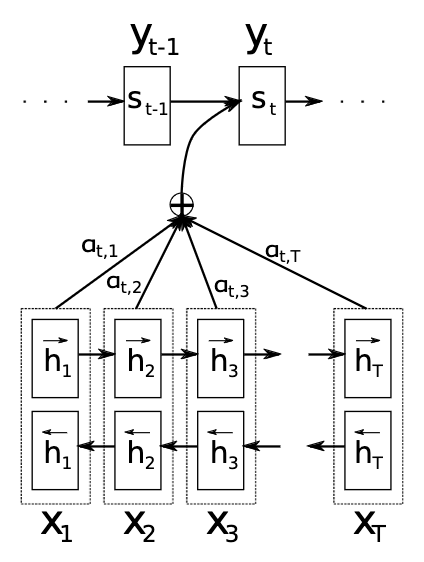
上記のようにAttentionではRNNの計算の際にそれぞれの層の重み付け和を計算し、この値を元に推論などを行います。このような計算を行うことで、「伝言ゲーム」のように伝達が難しいRNNの構造を改善させることが可能です。

Attentionの論文ではRNNに導入する形式でAttentionが用いられますが、TransformerではRNN構造を用いずに全体の処理を構築することからTransformerの論文のタイトルが「Attention Is All You Need」であることは有名な話です。

入門書ではRNNとLSTMが分けて解説されることもありますが、論文などではLSTMもrecurrent(再帰的)な構造であることからLSTMを含めてRNNと表されることが多いので注意が必要です。Attentionの基本事項は「深層学習による自然言語処理」の$4$章が詳しいので下記を参照ください。

グラフニューラルネットワークの基本式

Transformerの理解にあたってはグラフニューラルネットワークの数式を抑えておくと良いです。以下、理解しやすさの観点からMPNN(Message Passing Neural Network)の数式を主に参考に作成を行いました。
$$
\large
\begin{align}
m_{v}^{t+1} &= \sum_{w \in N(v)} M_{t}(h_{v}^{t}, h_{w}^{t}, e_{vw}) \\
h_{v}^{t+1} &= U_{t}(h_{v}^{t}, m_{v}^{t+1})
\end{align}
$$

上記の式はMPNN(Message Passing Neural Network)論文の$(1), (2)$式をそのまま表しました。上記の理解にあたっては下記の点に注意すると良いです。

① ノード$v$の隠れ層$h_{v}^{t}$について取り扱う式である。隠れ層はそれぞれのノードにWord$2$vecのように数十〜数百の要素を持つベクトルが割り当てられたと考えれば良い。
② ノード$v$の隣接ノードの集合を$N(v)$と表し、$w \in N(v)$であるので隣接するノードは個々の$w$で表される。$\displaystyle \sum_{w \in N(v)}$の表記は$N(v)$の全ての要素に関する$M_{t}(h_{v}^{t}, h_{w}^{t}, e_{vw})$の和を取るという意味である。
③ $m_{v}^{t+1}$は隣接するノードの隠れ層のベクトルを元に計算する式を表す。たとえば駅間で乗客が移動するようにイメージすれば良い。この処理をMessage Passingと呼称するが、Attention処理における重み付け和の計算はこの処理の一例と解釈できる。
④ $2$式目の$U_t$はMessage Passing処理で集約したMessageを元にノード$v$の隠れ層をUpdateする関数を定義したものである。Transformerで用いられるMLP(Multi Layer Perceptron)処理はこの一例である。
⑤ $t$や$t+1$はニューラルネットワークのレイヤーに対応する。よって$l, l+1$を用いて表すこともあり得る。
⑥ $n$層のグラフニューラルネットワークを取り扱う際は$h_{v}^{t+n}$を全てのノードに関して計算し、「ノード単位の分類」や「グラフ全体の分類」などの処理を行う。
⑦ Transformerではグラフ全体の$h_{v}^{t+n}$を用いてその後の処理を実行する。オリジナルのTransformerでは翻訳タスクに用いられたが、BERTなどのように様々な応用事例がある。

MPNNフレームワークに基づくグラフニューラルネットワークの詳細や具体例に基づく式の解釈に関しては下記でまとめましたので、詳しくは下記をご確認ください。

グラフニューラルネットワーク(GNN; Graph Neural Network)入門

Transformerの仕組み

Self-Attention

前節で確認したAttentionは非常に有力な処理モジュールである一方で、Attentionの処理における重みパラメータをどのように作成するかの手順を用意する必要があります。パラメータを外部から与える場合もあり得ますが、処理が複雑化し汎用的なモジュールになりにくいです。

上記に対し内部処理にAttentionの重みパラメータを計算するモジュールを用意するとシンプルに計算を行うことができます。このように通常の内部計算と同時にAttentionの重みパラメータを計算する仕組みをSelf-Attentionといいます。

Dot Product Attention

Self-Attentionの構造を実現させるにあたっては様々な計算方法がありますが、シンプルな手法の$1$つにDot Product Attentionがあります。ここでDot Product Attentionの「Dot Product」は内積を意味することは抑えておくと良いです。

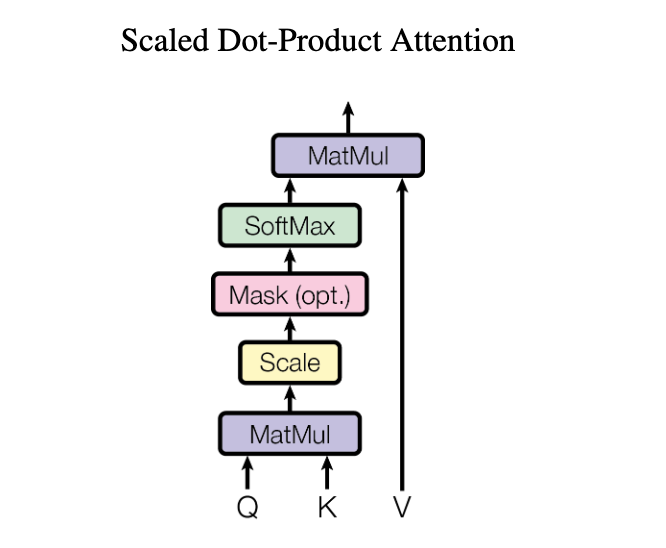
上図はTransformer論文における「Dot Product Attention」の処理を表しますが、QとKのmatmulの所で内積の計算を行い、その結果に基づいてVへのAttentionを計算すると解釈することができます。この処理は「ネットワーク分析」のグラフ作成と同様に理解することができます。

「ネットワーク分析」では単語のcos類似度の計算を行いグラフ化を行いましたが、cos類似度の計算は内積をそれぞれのベクトルの大きさで割ることで計算できるので、Dot Product Attentionの処理は概ねcos類似度の計算と同様な処理であると解釈できます。

RNN・Dot Product Attentionのグラフ理論に基づく解釈

RNNが直列的に表される処理である一方で、Dot Product Attentionは単語類似度に基づくグラフを元に表される処理であると解釈できます。

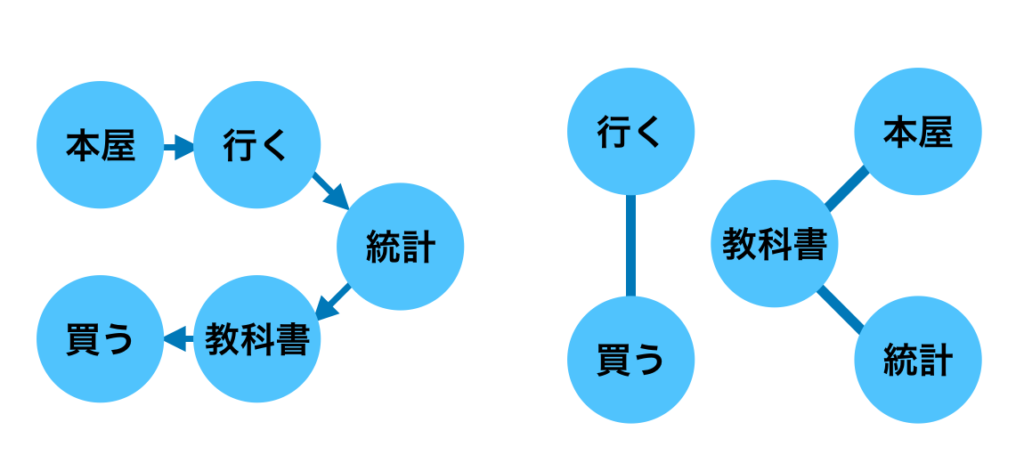
上図の例では単語が少ないのでどちらもそれほど大差ないように見えますが、右のように意味に基づくグラフを生成した上でRNNと同様にMLP処理を行う場合は、系列が$50$以上の場合も構造的に無理のない処理を行うことができます。

Multi Head Attention

Multi Head Attentionの解釈は一見難しいですが、基本的にはこれまでの処理を「並列で複数行う」と同義なので「アンサンブル学習」を行なったと解釈すれば良いです。Transformerにおけるグラフの構築は入力値に基づいて行われるので、並行処理で様々な結果が得られる可能性があります。

したがって、Multi Headを用いることで「ランダムフォレスト」のような「アンサンブル学習」と同様に計算のロバスト化を行うことができると解釈すると良いのではないかと思います。

Multi Head AttentionではたとえばWord$2$Vecの$512$次元を$8$分割し、それぞれ$64$次元ずつを元にDot Product Attentionの処理を行うようにイメージすれば良いです。

ランダムフォレストでは個々の学習器の学習の際に表型のデータから列と行をランダムに抜き出すことで相関の低い決定木を作成しますが、Multi Head AttentionではWord$2$Vecのベクトルを分割することでそれぞれ相関の低い計算結果を構築することができます。

また、この分割や再連結はTransformer論文ので下記のような数式で表されるパラメータ処理を行うことが一般的です。
$$
\large
\begin{align}
\mathrm{MultiHead}(Q,K,V) &= \mathrm{Concat}(\mathrm{head}_{1}, \cdots , \mathrm{head}_{h}) W^{O} \\
\mathrm{head}_{i} &= \mathrm{Attention}(QW_{i}^{Q}, KW_{i}^{K}, VW_{i}^{V}) \\
W_{i}^{Q} & \in \mathbb{R}^{d_{model} \times d_{k}}, \, W_{i}^{K} \in \mathbb{R}^{d_{model} \times d_{k}}, W_{i}^{V} \in \mathbb{R}^{d_{model} \times d_{v}}
\end{align}
$$

式は難しく見えますが、基本的には相関の低い結果を元にアンサンブル学習を行うランダムフォレストと同様に解釈しておければ十分だと思います。

グラフニューラルネットワークとTransformer

Transformerはグラフニューラルネットワークの一種と見なすと理解しやすいです。グラフニューラルネットワークではグラフが与えられた際に隣接するノードの持つ隠れ層の和などを計算することによってグラフに沿って伝達を行い、それぞれの隠れ層に関してMLP処理を行います。

RNNはグラフニューラルネットワークの一種であり、Recurrent(再帰)処理は一方向かつ一直線のグラフであると解釈することができます。

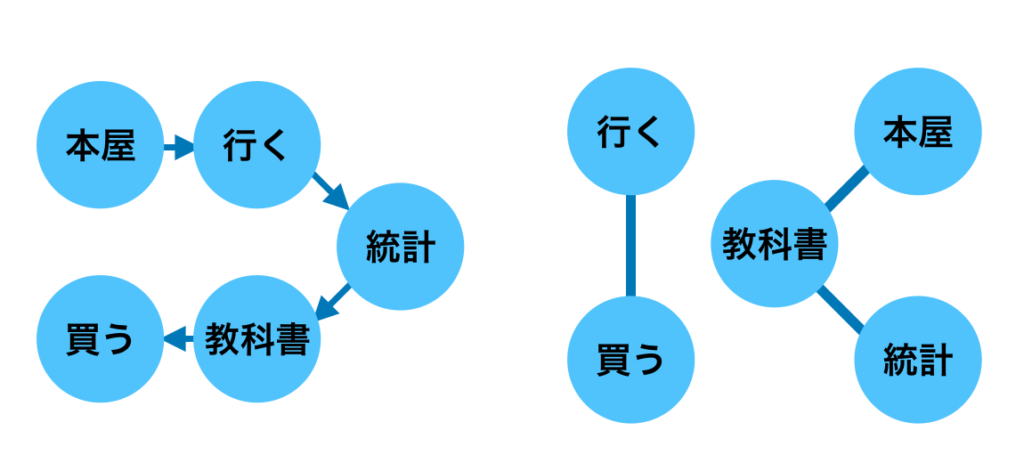
図の左のようなグラフに沿ってRNNの計算処理が行われるのと同様に、グラフニューラルネットワークでは上図の右のようにグラフが与えられ、それぞれ隣接するノードに基づいて和などの計算を行います。

基本的にグラフニューラルネットワークでは「①グラフに基づくノード間の伝達処理」と「②ノード毎のMLP処理」で構成されます。

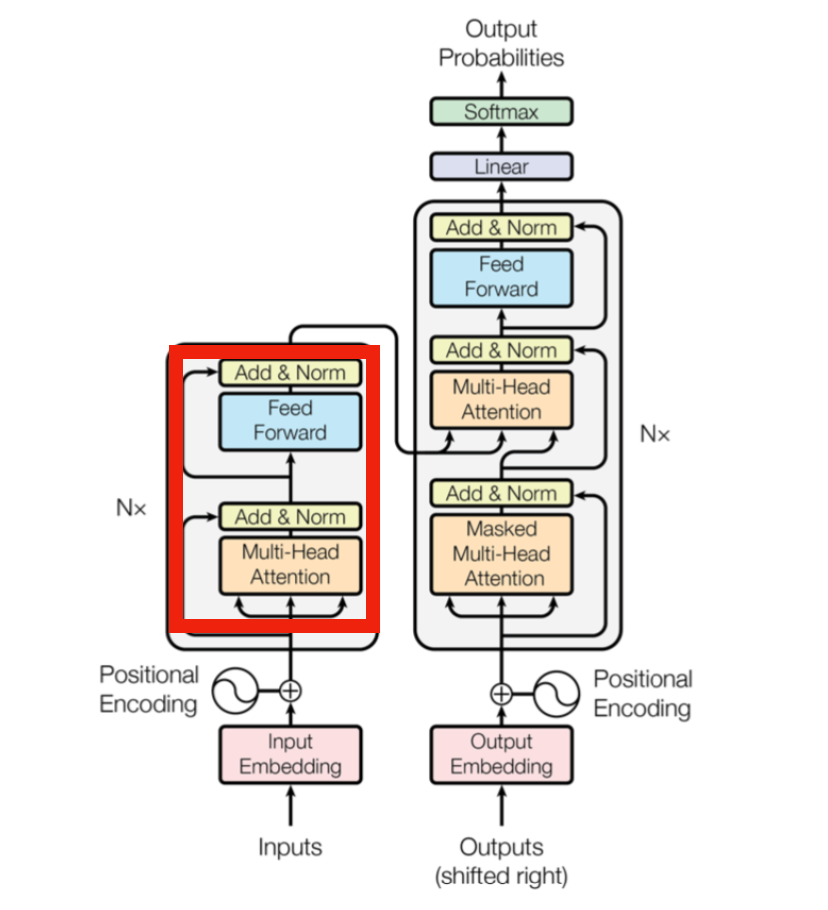
Transformerは上記の赤枠のようにMulti-Head AttentionとFeed Forwardで構成されており、Multi-Head Attentionを構成するDot Product Attentionがネットワーク分析と同様にグラフを構築しグラフに基づいて相互に伝達を行う処理、Feed ForwardがMLP(Multi Layer Perceptron)処理であると解釈することができます。このように考えることでTransformerは単語類似度を元に構築されるグラフを用いたグラフニューラルネットワークであると解釈できます。

Transformerにおける学習パラメータは一見わかりにくいですが、Multi-Head AttentionではなくFeed Forward部分で行われることも注意して確認しておくと良いです。

グラフニューラルネットワークの定義は論文によって様々ではありますが、MPNN(Message Passing Neural Network)やNLNN(Non Local Neural Network)の論文などを元に理解するとわかりやすいのではないかと思います。

グラフニューラルネットワークとRNN

RNNはグラフニューラルネットワークの一種と考えることもできますが、グラフニューラルネットワークは近年のトピックであることからグラフニューラルネットワークはRNNの拡張であると見なすこともできます。

グラフを用いて参照構造を表す試みによって、多くのDeepLearningの構造が抽象化可能であるのでグラフニューラルネットワークの概要は抑えておくと良いと思います。

また、単に外からグラフを与えるだけでなくTransformerのように内部処理でグラフを作成することで、グラフを用意する必要がないというのはなかなか強力です。

Transformerの構造に関する主要研究

Reformer

MLP-Mixer

まとめ

当記事の内容は下図のようにまとめることができます。

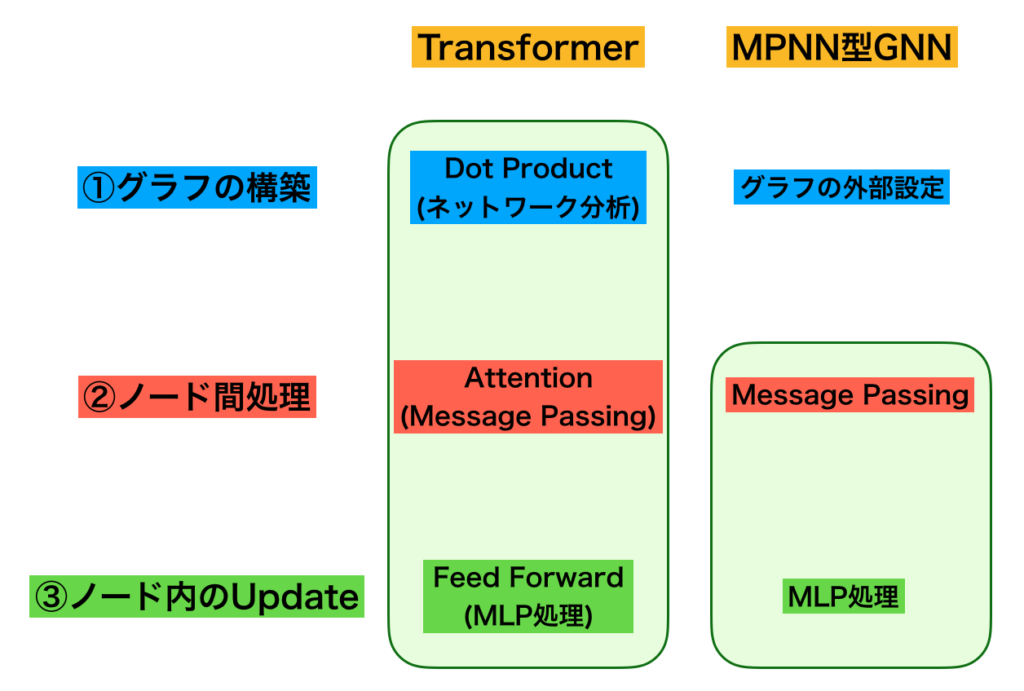
Transformerの各層では主に「①グラフの構築」、「②ノード間処理」、「③ノード内のUpdate」の$3$つの処理が行われており、①は「ネットワーク分析」、②と③は「MPNN型のグラフニューラルネットワーク」の処理に対応すると解釈すると理解しやすいです。

参考

・Transformer論文
・Word$2$vec論文①
・Word$2$vec論文②
・Attention論文
・MPNN論文
・NLNN論文
・Reformer論文
・MLP-Mixer論文
・直感的に理解するTransformer(運営者作成)
・グラフ理論と機械学習(運営者作成)
・Pythonで理解する言語処理(運営者作成)