当記事では「統計学を学ぶにあたって最低限抑えておきたい数学」の中から「ベクトルの基本と内積」に関して取り扱います。ベクトルは複数の数字を同時に取り扱う考え方で、多次元の変数を取り扱う際などに必須になるので抑えておくと良いです。
取りまとめにあたっては数学の解説に関してはなるべくシンプルに取り扱いますが、統計学への応用に関連した複雑な内容に関しては目次に「*」をつけました。「*」がついているものはやや難しいので、読み飛ばしても問題ありません。
・基本数学まとめ
https://www.hello-statisticians.com/math_basic
Contents
ベクトルの基本
ベクトルの概要
ベクトルは「大きさ」と「向き」の$2$つで表される概念です。たとえば強風の注意報が出る場合はどの方角か以上に「秒速$x$m/s」が重要である一方で、夏や冬の雨量や積雪量の予報にあたっては「季節風がどの方角から吹くか」が「秒速$x$m/s」と同様に重要になります。
風速の例と同様に、単に「大きさ」を知れば良い場合と、「向き」も含めて重要な場合が色々とあります。このような場合に「大きさ」と「向き」を同時に取り扱う概念が「ベクトル」です。
ベクトルの式表記
ベクトルの式表記にあたっては数ⅡBでは$\vec{x}$のように表されることが多いです。一方、線形代数などではボールド体を用いて$\mathbf{x}$のように表される場合が多いですが、線形代数的な式変形がメインでない場合は$\vec{x}$を用いるで良いと思います。
ベクトルは「向き」と「大きさ」を取り扱う量であるので、$\vec{x}$の大きさを表す表記があると使いやすいです。このような際には$|\vec{x}|$のように表されることが多いです。
ベクトルの成分表示
前項のようにベクトルは$\vec{x}$のように定義されますが、ベクトルを$x$-$y$平面上の成分で表示することで様々な応用に用いることができます。具体的には下記のようにベクトルの成分表示を行うことができます。
import numpy as np
import matplotlib.pyplot as plt
x = np.array([1., 2.])
loc = np.zeros(2)
plt.quiver(loc[0], loc[1], x[0], x[1], color="green", angles="xy", scale_units ="xy", scale=1)
plt.grid()
plt.xlim(-1, 2)
plt.ylim(-1, 3)
plt.show()・実行結果
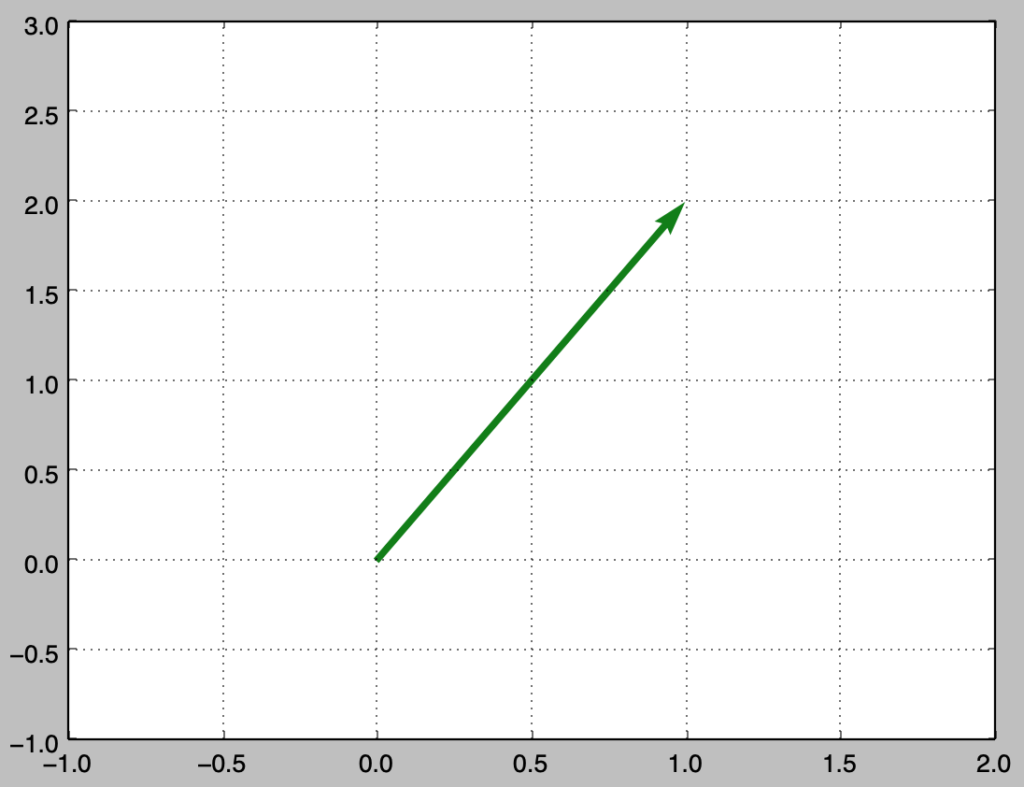
上記は$\vec{x}=(1, 2)$に対応します。上記は$x$-$y$平面上の成分に対応しますが、$x$-$y$-$z$空間上の成分に対応させて$3$次元で描画を行うことも可能です。また、ベクトルの成分表記は$\vec{x}=(1, 2)$のように横に書かずに下記のように縦に表記することもできます。
$$
\large
\begin{align}
\vec{x} &= \left(\begin{array}{c} 1 \\ 2 \end{array} \right) \\
\vec{y} &= \left(\begin{array}{c} 1 \\ 2 \\ 3 \\ 4 \\ 5 \end{array} \right)
\end{align}
$$
ベクトルの加減
当項ではベクトルの加減について取り扱います。
$$
\large
\begin{align}
\vec{x} &= \left(\begin{array}{c} 2 \\ 1 \\ 2 \end{array} \right) \\
\vec{y} &= \left(\begin{array}{c} 1 \\ 2 \\ 3 \end{array} \right)
\end{align}
$$
上記のように定めた$\vec{x}, \vec{y}$に関して下記のように計算を行うことができます。
$$
\large
\begin{align}
\vec{x}+\vec{y} &= \left(\begin{array}{c} 2 \\ 1 \\ 2 \end{array} \right) + \left(\begin{array}{c} 1 \\ 2 \\ 3 \end{array} \right) = \left(\begin{array}{c} 3 \\ 3 \\ 5 \end{array} \right) \\
\vec{x}-\vec{y} &= \left(\begin{array}{c} 2 \\ 1 \\ 2 \end{array} \right) – \left(\begin{array}{c} 1 \\ 2 \\ 3 \end{array} \right) = \left(\begin{array}{c} 1 \\ -1 \\ -1 \end{array} \right)
\end{align}
$$
「ベクトルの成分表示」にあたっては横表記、縦表記のどちらも用いることができますが、上記のような演算を行う際には縦表記を用いると計算が見やすいです。
ベクトルのスカラー積
当項ではベクトルのスカラー積について取り扱います。ベクトルの積には主にスカラー積、内積、外積がありますが、スカラー積は当項で、内積は次節で取り扱います。外積は当記事では省略します。
$$
\large
\begin{align}
\vec{x} &= \left(\begin{array}{c} 1 \\ 2 \\ 3 \end{array} \right)
\end{align}
$$
上記のように定義した$\vec{x}$に関して下記のようにスカラー積の計算を行うことができます。
$$
\large
\begin{align}
2\vec{x} &= 2 \left(\begin{array}{c} 1 \\ 2 \\ 3 \end{array} \right) \\
&= \left(\begin{array}{c} 2 \\ 4 \\ 6 \end{array} \right)
\end{align}
$$
内積
内積の概要
前節ではベクトルとスカラーの積について取り扱いましたが、当項ではベクトルとベクトルの積について取り扱います。ベクトルとベクトルの積を考えるにあたっては主に内積と外積がありますが、以下、内積について取り扱います。
ベクトル$\vec{x}, \vec{y}$の内積$\vec{x} \cdot \vec{y}$は$2$つのベクトルのなす角$\theta$を用いて下記のように定義します。
$$
\large
\begin{align}
\vec{x} \cdot \vec{y} = |\vec{x}| |\vec{y}| \cos{\theta}
\end{align}
$$
次に以下のように$\vec{x}, \vec{y}$が成分表示ができると仮定します。
$$
\large
\begin{align}
\vec{x} &= \left(\begin{array}{c} x_1 \\ x_2 \end{array} \right) \\
\vec{y} &= \left(\begin{array}{c} y_1 \\ y_2 \end{array} \right)
\end{align}
$$
このとき内積は下記のように表すことができます。
$$
\large
\begin{align}
\vec{x} \cdot \vec{y} &= \left(\begin{array}{c} x_1 \\ x_2 \end{array} \right) \cdot \left(\begin{array}{c} y_1 \\ y_2 \end{array} \right) \\
&= x_1 y_1 + x_2 y_2
\end{align}
$$
ベクトルの類似度と内積
「ベクトルが同じ向きを向くか」を判断する際の指標に$2$つのベクトルのなす角の$\cos{\theta}$を用いることができます。内積の定義の式を$\cos{\theta}$に関して解くと下記が得られます。
$$
\large
\begin{align}
\vec{x} \cdot \vec{y} &= |\vec{x}| |\vec{y}| \cos{\theta} \\
\cos{\theta} &= \frac{\vec{x} \cdot \vec{y}}{|\vec{x}| |\vec{y}|}
\end{align}
$$
上記を元に$\vec{x}$と$\vec{y}$の類似度を計算することができます。近年DeepLearningの領域でよく用いられるTransformerのDot Product Attentionは内積を元に処理を行うなど、内積の応用例は多いので、式定義は抑えておくと良いと思います。
