状態空間モデルシリーズでは複数の記事に分けて、時系列データを扱う柔軟なモデルである状態空間モデル(State Space Model) を解説します。
前回(第2回)では、状態空間モデルの定式化を行い、時系列データの複雑な依存関係を以下の確率的表現で記述できることを示しました。
$$
\begin{aligned}
x_t &\sim p(x_t | x_{t-1}) \\
y_t &\sim p(y_t | x_t)
\end{aligned}
$$
ここで、一つ目の式がシステムモデル、二つ目が観測モデルと呼ばれています。
第3回である本記事では、この状態空間モデルを用いた推定問題を扱います。具体的には、観測データ$y_{1:T}$ から隠れた状態 $x_t$ を推定するベイズフィルタの理論的枠組みを解説します。今回は数式が多めですが、特に難しいことはやらないので、落ち着いて読んでみてください。
Contents
ベイズフィルタの理論的枠組み
確率モデルから推定問題へ
前回記事では、時刻$1$から$T$までの状態ベクトル$x_{1:T}$と観測データ $y_{1:T}$ の確率モデルとして下記の同時分布を導出した。
$$
p(x_{1:T}, y_{1:T}) = \prod^T_{t-1} p(y_t | x_{t}) p( x_t | x_{t-1} )
$$
推定問題を考えると、観測データ $y_{1:T}$ は既知のデータとなる(実際に観測できるデータ)。一方、状態 $x$ (季節調整モデルでは、トレンド成分と季節成分のベクトル) が未知であり、この状態ベクトルを推定することが目的となる。
この推定問題は、下記の条件付き分布を求めることになる。
$$
p(x_{1:T} | y_{1:T}) = \frac{p(x_{1:T}, y_{1:T})}{p(y_{1:T})}
$$
計算上の課題
しかしながら、 $p(x_{1:T} | y_{1:T})$ を直接計算することは、一般的に困難である。主な理由は下記の通り。
- 状態系列全体の同時分布は高次元: 状態系列全体 $x_{1:T}$ の結合分布は高次元となり、解析的な計算が困難
- 周辺化計算: 分母の $p(y_{1:T}) = \int p(x_{1:T}, y_{1:T}) dx_{1:T}$ は高次元積分となる
- 計算複雑度: $T$ が大きくなると計算量が指数的に増加
- リアルタイム性: 新しい観測が得られるたびに全体を再計算する必要
3つの重要な事後分布
そのため通常、時刻毎の事後分布を逐次的に計算するというアプローチがとられる。つまり、時刻 $t$ の状態 $x_t$ の事後分布 $p(x_t | y_{1:t’})$ を取り扱う。ここで $t’$ は、$1 \leq t’ \leq T$ の任意の範囲をとる。
このように $t$ 時刻の状態 $x_t$ の推定問題とすることで、マルコフ性が成り立つ構造の場合には漸化式を用いて逐次的に事後分布 $p(x_t | y_{1:t’})$ を計算することが可能になる。事後分布は $t’$ の範囲によって下記の3つの分布に分けられる。
- 予測分布: $p(x_t | y_{1:t-1})$
- 時刻t-1までの観測 $y_{1:t-1}$ で時刻tの状態を予測する
- 1ステップ先の状態予測
- フィルタ分布: $p(x_t | y_{1:t})$
- 新たに時刻tの観測を追加し、 $y_{1:t}$ で時刻tの状態を更新する
- 現在時点のデータまで利用して予測を更新する
- 平滑化分布: $p(x_t | y_{1:T})$
- 全観測で時刻tの状態を更新する
- 未来の情報も活用して、事後的な状態修正
ベイズフィルタの状態更新フロー
予測分布($p(x_t | y_{1:t-1})$)とフィルタ分布($p(x_t | y_{1:t})$)を逐次的に計算していくことで、状態 $x_{1:T}$ を推定していく操作をベイズフィルタ(Bayesian filtering)と呼ぶ。
ベイズフィルタは以下の2ステップで状態推定を行う。
予測ステップ(Prediction Step)
前時刻のフィルタ分布$p(x_{t-1} | y_{1:t-1})$から状態遷移モデルを用いて次時刻の予測分布$p(x_{t} | y_{1:t-1})$を計算
更新ステップ(Update Step)
新しい観測値 $y_t$ を用いてベイズの定理により予測分布を更新($p(x_{t} | y_{1:t})$)
概念図は以下の通りとなる。

このように、予測と更新の2ステップを繰り返すことで、新しい観測が得られるたびに状態の推定を逐次的に改善していく。これがベイズフィルタの基本的な動作原理である。
予測分布の導出
ここでは、予測分布 $p(x_t | y_{1:t-1})$ が1期前のフィルタ分布 $p(x_{t-1} | y_{1:t-1})$ に基づいて計算されることを確認する。
予測分布 $p(x_t | y_{1:t-1})$ について、周辺化の逆操作を用いて以下のように展開する。
$$
\begin{aligned}
p(x_t | y_{1:t-1}) &= \int p(x_t, x_{t-1} | y_{1:t-1}) dx_{t-1} \\
&= \int p(x_t |x_{t-1}, y_{1:t-1}) p(x_{t-1} | y_{1:t-1}) dx_{t-1}
\end{aligned}
$$
このように、周辺化を逆に用いる変形は、周辺化と併せてよく用いられるテクニックなので、覚えておくと良い。また、2行目への変換には、条件付き確率の定義を適用している。
この2行目の式に、状態空間モデルのマルコフ性を適用する。マルコフ性により、現在の状態 $x_t$ は前状態 $x_{t-1}$ のみに依存し、それより過去の観測には直接依存しない。
$$
\begin{aligned}
p(x_t | y_{1:t-1}) = \int p(x_t |x_{t-1} ) p(x_{t-1} | y_{1:t-1}) dx_{t-1}
\end{aligned}
$$
$x_{t-1}$ を条件にすることで、過去の観測 $y_{1:t-1}$ が独立となる。
この式をよく見ると、右辺の積分の第1項 $p(x_t |x_{t-1} )$ がシステムモデルであり、第2項は時刻 $t-1$ のフィルタ分布 $p(x_{t-1} | y_{1:t-1})$ であることがわかる。つまり、予測分布は「前時刻の推定結果をシステムモデルで1ステップ先に伝播させた結果」として計算される。
フィルタ分布の導出
ここでは、フィルタ分布 $p(x_t | y_{1:t})$ が予測分布 $p(x_{t} | y_{1:t-1})$ に基づいて計算できることを確認する。
フィルタ分布 $p(x_t | y_{1:t})$ について、ベイズの定理を適用して展開する。
$$
\begin{aligned}
p(x_t | y_{1:t} ) &= p(x_t | y_t, y_{1:t-1}) \\
&= \frac{ p(x_t, y_t | y_{1:t-1}) }{ p(y_t | y_{1:t-1}) } \\
&= \frac{ p(y_t | x_t, y_{1:t-1}) p(x_t | y_{1:t-1}) }{ p(y_t | y_{1:t-1}) }
\end{aligned}
$$
次に、観測モデルの条件付き独立性を適用する。状態 $x_t$ が条件として与えられれば、観測 $y_t$ は過去の観測から独立になる($p(y_t | x_t, y_{1:t-1}) = p(y_t | x_t)$)。
$$
\begin{aligned}
p(x_t | y_{1:t} ) &= \frac{ p(y_t | x_t, y_{1:t-1}) p(x_t | y_{1:t-1}) }{ p(y_t | y_{1:t-1}) } \\
&= \frac{ p(y_t | x_t ) p(x_t | y_{1:t-1}) }{ p(y_t | y_{1:t-1}) }
\end{aligned}
$$
最後の式の分子を確認すると、第1項が観測モデルとなっており、第2項が予測分布になっていることがわかる。
では次に、上記の最後の式の分母 $p(y_t | y_{1:t-1})$ を確認する。
$$
\begin{aligned}
p(y_t | y_{1:t-1}) &= \int p(y_t, x_t | y_{1:t-1}) dx_t \\
&= \int p(y_t | x_t, y_{1:t-1}) p( x_t | y_{1:t-1}) dx_t \\
&= \int p(y_t | x_t ) p( x_t | y_{1:t-1}) dx_t
\end{aligned}
$$
1つ目の式は周辺化を逆に適用している。2つ目の式はベイズの定理(同時分布と条件付き分布の変換)を利用しており、3つ目の式はマルコフ性を適用している。
最後の式を確認すると、これは先に計算した、フィルタ分布の展開式の分子をそのまま積分していることがわかる。つまり、正規化を意味している。
これらをまとめると、フィルタ分布は以下のように、観測モデル $p(y_t | x_t )$ と予測分布 $p(x_{t} | y_{1:t-1})$ に基づいて計算できることがわかる。
$$
\begin{aligned}
p(x_t | y_{1:t} ) &= \frac{ p(y_t | x_t ) p(x_t | y_{1:t-1}) }{ \int p(y_t | x_t ) p( x_t | y_{1:t-1}) dx_t } \\
&= \propto p(y_t | x_t ) p(x_t | y_{1:t-1})
\end{aligned}
$$
この式は、ベイズ推論の標準的な形「事後分布 ∝ 尤度 × 事前分布」そのものである。
平滑化分布の導出
最後に平滑化分布 $p(x_t | y_{1:T})$ について扱う。
全期間 $t = 1, 2, \cdots, T$ の観測データ $y_{1:T}$ が既に得られている状況を考える。
最終時刻 $T$ においては、利用可能な観測データが $y_{1:T}$ 、つまり全てであるため、時刻Tのフィルタ分布 $p(x_T | y_{1:T})$ は平滑化分布と一致する。
任意の時刻 $t$ の平滑化分布 $p(x_t | y_{1:T})$ は、上記の境界条件から出発して後向きに再帰的に計算される。
$$
p(x_T | y_{1:T}) \rightarrow p(x_{T-1} | y_{1:T}) \rightarrow \cdots \rightarrow p(x_1 | y_{1:T})
$$
この後向き再帰の漸化式を導出することで、任意の時刻 $t$ の平滑化分布 $p(x_t | y_{1:T})$ を求めることができる。
以下では、この漸化式の導出過程を示す。
グラフィカルモデルと d-分離(d-separation)
漸化式の導出に入る前に鎖状構造グラフィカルモデルとd-分離という重要な性質を扱う。
グラフィカルモデルとは、確率変数をノードに、変数間の関係をエッジで表現したグラフである。特にエッジに向きがあるグラフは有向グラフと呼ばれ、確率変数間の依存関係の方向を表現できる。
本稿では下記の状態空間モデルを扱っている
$$
\begin{aligned}
x_t &\sim p(x_t | x_{t-1}) \\
y_t &\sim p(y_t | x_t)
\end{aligned}
$$
状態空間モデルの式を確率変数 $x, y$ の依存関係として見ると、 $x_t$ は $x_{t-1}$ にのみ依存し、$y_t$ は $x_t$ にのみ依存するという構造であることがわかる。このような関係をグラフィカルモデルで表現すると下記のような構造で表せることができる。
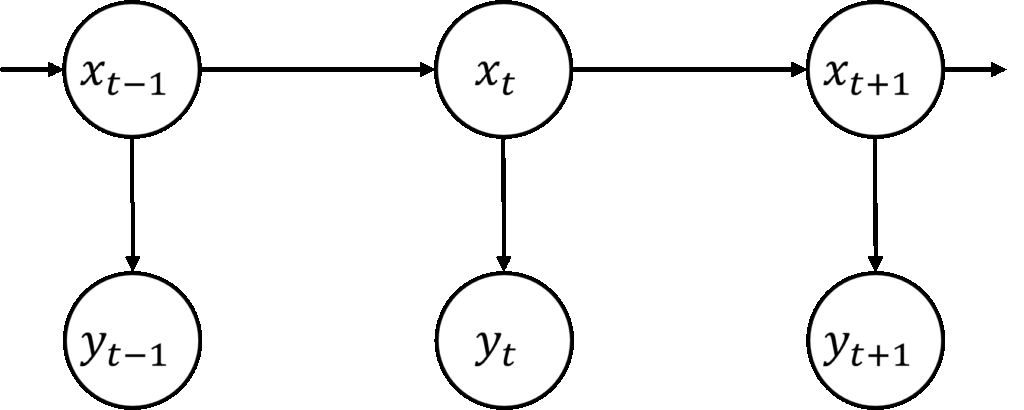
状態空間モデルは時刻 $t$ が進むにつれ、上記の図の構造が時間方向に延びていく。このようなグラフィカルモデルを特に鎖状構造グラフィカルモデルと呼ぶ。
グラフィカルモデルの重要な性質として、d-分離がある。d-分離とは、例えば$x_t$ について考えたとき、 $x_{t+1}$ が与えられている(固定の値)とみると、 $x_t$ は未来の観測 $y_{t+2}, y_{t+3}, \cdots$ から条件付き独立になるという性質である。 $x_{t+1}$ が情報の流れを遮断するため、このような性質が表れる。
$x_{t+1}$ から繋がる矢印、 $y_{t+1}$ や $x_{t+2}$ は $x_t$ に影響を及ぼさない。
この性質を利用して平滑化分布の漸化式を導出する。
漸化式の導出
平滑化分布の漸化式の導出にあたって、 $x_t, x_{t+1}$ の漸化式を導出する。まず、 $p(x_t | y_{1:T})$ について周辺化の逆操作を利用し、$x_t, x_{t+1}$ の同時分布を構築し、確率の乗法定理を利用して整理する。
$$
\begin{aligned}
p(x_t | y_{1:T}) &= \int p(x_t, x_{t+1} | y_{1:T}) dx_{t+1} \\
&= \int p(x_t | x_{t+1}, y_{1:T}) p(x_{t+1} | y_{1:T}) dx_{t+1}
\end{aligned}
$$
ここで、2つ目の式の第1項である $ p(x_t | x_{t+1}, y_{1:T})$ について、 $ x_{t+1}$ が所与となるので、鎖状構造グラフィカルモデルでのd-分離を適用する。
$$
p(x_t | x_{t+1}, y_{1:T}) = p(x_t | x_{t+1}, y_{1:t})
$$
図で表現すると以下のように、 $x_{t+1}$ が所与(固定の値)となるので、$y_{t+1}$ 以降(緑の領域)が分離できることがわかる。
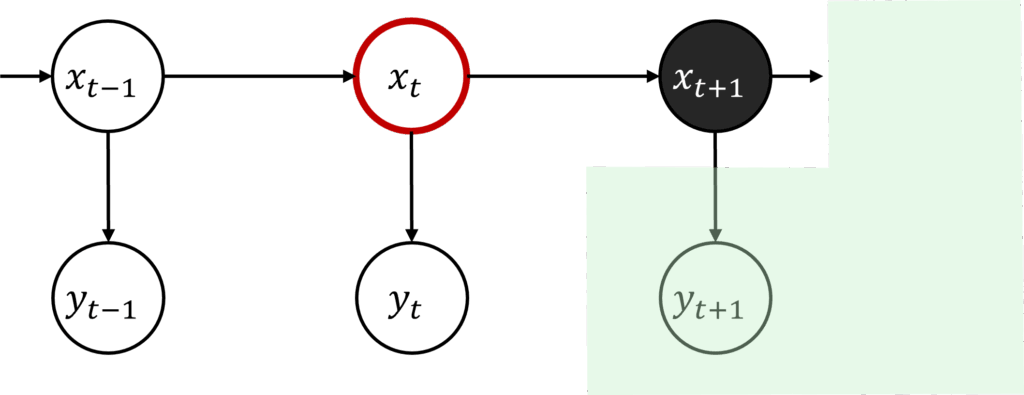
この結果を利用して、漸化式の続きを導出していく(複雑な式展開に見えるかもしれないが、それぞれの式は基本的な性質を適用しているだけなので、一つずつ見ていけば難しくはない)
$$
\begin{aligned}
p(x_t | y_{1:T}) &= \int p(x_t | x_{t+1}, y_{1:t}) p(x_{t+1} | y_{1:T}) dx_{t+1} \\
&= \int \frac{ p(x_t, x_{t+1} | y_{1:t}) }{ p(x_{t+1} | y_{1:t} ) } p(x_{t+1} | y_{1:T}) dx_{t+1} \\
&= \int \frac{ p(x_{t+1} | x_t, y_{1:t}) p(x_t | y_{1:t}) }{ p(x_{t+1} | y_{1:t} ) } p(x_{t+1} | y_{1:T}) dx_{t+1} \\
&= \int \frac{ p(x_{t+1} | x_t) p(x_t | y_{1:t}) }{ p(x_{t+1} | y_{1:t} ) } p(x_{t+1} | y_{1:T}) dx_{t+1} \\
&= p(x_t | y_{1:t}) \int \frac{ p(x_{t+1} | x_t) }{ p(x_{t+1} | y_{1:t} ) } p(x_{t+1} | y_{1:T}) dx_{t+1}
\end{aligned}
$$
2つ目の式と3つ目の式は、確率の乗法公式を適用している。4つ目の式は、マルコフ性を適用している。最後の式は、積分に関係ない項を積分の外に出している。
この式を確認すると、フィルタ分布 $p(x_t | y_{1:T})$ は、$t+1$ の平滑化分布 $p(x_{t+1} | y_{1:T})$ と、$t$ のフィルタ分布 $p(x_t | y_{1:t})$ 、$t+1$ の予測分布 $p(x_{t+1} | y_{1:t}$ 、システムモデル $p(x_{t+1} | x_t)$ で計算することができることがわかった。
まとめ
今回は、状態空間モデルを用いた状態推定の問題に取り組んだ。状態推定とは、観測データ$y_{1:t’}から隠れた状態 $x_t$ の事後分布を求める問題である。利用できる観測値 $y_{1:t’}$ の範囲によって以下の3つの事後分布に分類される。
- 予測分布: $p(x_t | y_{1:t-1})$
- 時刻t-1までの観測 $y_{1:t-1}$ で時刻tの状態を予測する
- 1ステップ先の状態予測
- フィルタ分布: $p(x_t | y_{1:t})$
- 新たに時刻tの観測を追加し、 $y_{1:t}$ で時刻tの状態を更新する
- 現在時点のデータまで利用して予測を更新する
- 平滑化分布: $p(x_t | y_{1:T})$
- 全観測で時刻tの状態を更新する
- 未来の情報も活用して、事後的な状態修正
特に、予測分布とフィルタ分布を2段階(予測ステップ、更新ステップ)で逐次的に計算する手法をベイズフィルタと呼ぶ。この枠組みにより、新しい観測が得られるたびに状態推定を効率的に更新できる。
また、全ての観測値が得られた後に、事後的に状態を更新する(平滑化)場合にも、逐次的な計算で平滑化分布が導出できることがわかった。
ベイズフィルタを利用することで状態 $x_t$ の事後分布を導出することができるわけだが、現実の問題を扱う場合、解析的に事後分布を導出できることは稀である。そのため、モデルに線形の仮定を設けたり、計算的に近似推定を行うことが多い。
次回は、モデルに線形ガウスの仮定を置くことで、解析的な解を導出するカルマンフィルタを扱う。
