統計的仮説検定における有意水準$\alpha$と検出力$1-\beta$はそれぞれ第$1$種の過誤と第$2$種の過誤の度合いを調整する指標であり、これらの値に基づいてサンプルサイズの設計を行うことが可能です。当記事では有意水準と検出力からサンプルサイズ設計を行う一連の流れに関して取りまとめを行いました。
「統計検定準$1$級対応 統計学実践ワークブック」のCh.$10$「検定の基礎と検定法の導出」を主に参考に作成を行いました。
・統計学実践ワークブック Ch.$10$ 「検定の基礎と検定法の導出」まとめ
https://www.hello-statisticians.com/explain-books-cat/stat_workbook/stat_workbook_ch10.html
有意水準$\alpha$と検出力$1-\beta$
有意水準$\alpha$
帰無仮説$H_0$が正しいにも関わらず棄却する確率を有意水準(significance level)といい、$\alpha$で表すことが多い。以下、標準正規分布を元に確認を行う。下記では両側$5$%を考える際の上側の棄却域の描画を行なった。
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
alpha = 0.05
x0 = np.arange(-5., 5.01, 0.01)
y0_pdf = stats.norm.pdf(x0)
x0_upper = stats.norm.ppf(1.-alpha/2.)
reject_x0 = x0[x0 >= x0_upper]
reject_y0 = stats.norm.pdf(reject_x0)
plt.plot(x0, y0_pdf, color="blue")
plt.fill_between(reject_x0, reject_x0*0., reject_y0, color="blue", alpha=0.3)
plt.show()・実行結果
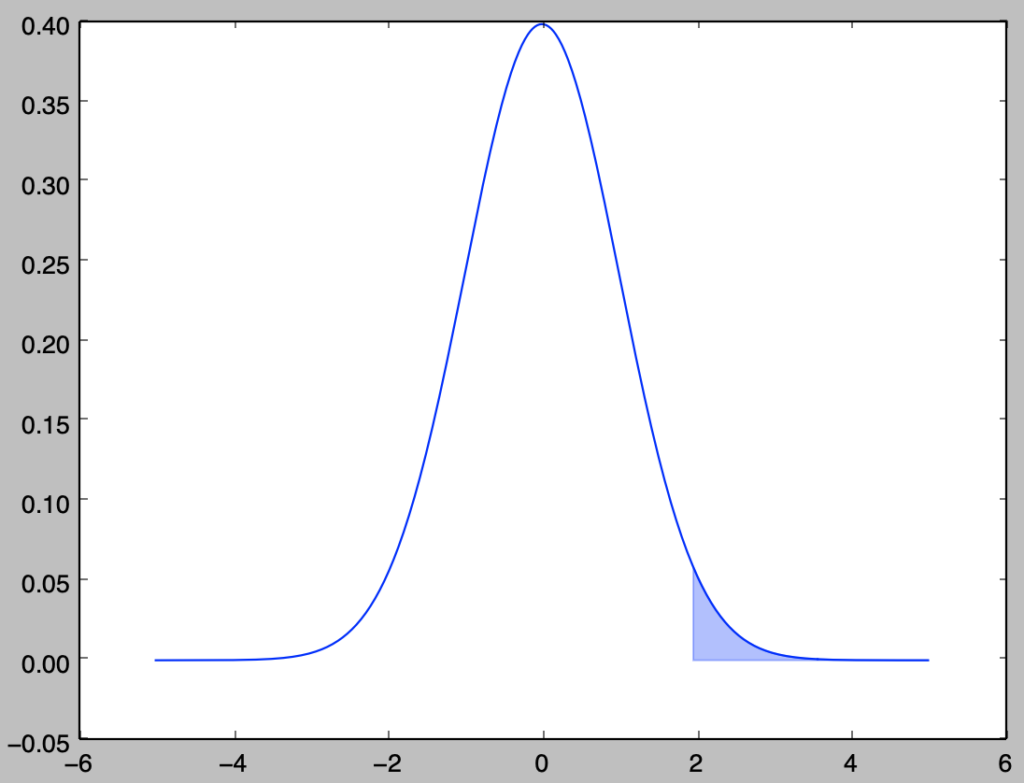
標準正規分布を用いる統計的仮説検定では、基本的に検定統計量$Z$が$Z \sim \mathcal{N}(0,1)$のように標準正規分布に従うと考え、結果の検証を行う。
検出力$1-\beta$
有意水準$\alpha$は「帰無仮説$H_0$を棄却するかどうか」の指標であり、「対立仮説$H_1$の真偽」に関しては別途考える必要がある。「帰無仮説$H_0$」と「対立仮説$H_1$」に基づく$2$値分類では下記の$4$パターンの状況が起こりうる。
| 状況 | 決定$D$ | 母数$\Theta$ | 正誤 |
|---|---|---|---|
| ① | $H_0$を棄却 | 実際は$H_1$が正しい | ◎ |
| ② | $H_0$を棄却 | 実際は$H_0$が正しい | × |
| ③ | $H_0$を受容 | 実際は$H_1$が正しい | × |
| ④ | $H_0$を受容 | 実際は$H_0$が正しい | ◎ |
このとき通常の統計的仮説検定では②の過誤を重視し有意水準を定め、③の過誤に関してはそれほど考えない。このことは統計的仮説検定で取り扱う問題設定に起因し、重大な決断などを行う際に「決定によるマイナス」が「決定しないマイナス」以上に遥かに大きい場合などを例に考えるとわかりやすい。
一方で、③の過誤に関して全く考えないというのも不合理であるので、③の過誤について取り扱う指標に検出力がある。検出力は「有意水準$\alpha$の仮説検定を行う際」に「$H_1$が正しいときに$H_0$を棄却する確率」を定める指標である。
下記では$H_0$が$Z \sim \mathcal{N}(0,1)$、$H_1$が$Z \sim \mathcal{N}(3,1)$に従うと考える場合に、$\alpha=5$%の両側検定を行うという前提での有意水準と検出力の図示を行なった。
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
alpha = 0.05
x0 = np.arange(-5., 5.01, 0.01)
y0_pdf = stats.norm.pdf(x0)
x1 = np.arange(-2., 8.01, 0.01)
y1_pdf = stats.norm.pdf(x1,loc=3.)
x0_upper = stats.norm.ppf(1.-alpha/2.)
reject_x0 = x0[x0 >= x0_upper]
reject_y0 = stats.norm.pdf(reject_x0)
reject_x1 = x1[x1 <= x0_upper]
reject_y1 = stats.norm.pdf(reject_x1, loc=3.)
plt.plot(x0, y0_pdf, color="blue")
plt.fill_between(reject_x0, reject_x0*0., reject_y0, color="blue", alpha=0.3)
plt.plot(x1, y1_pdf, color="green")
plt.fill_between(reject_x1, reject_x1*0., reject_y1, color="green", alpha=0.3)
plt.show()・実行結果
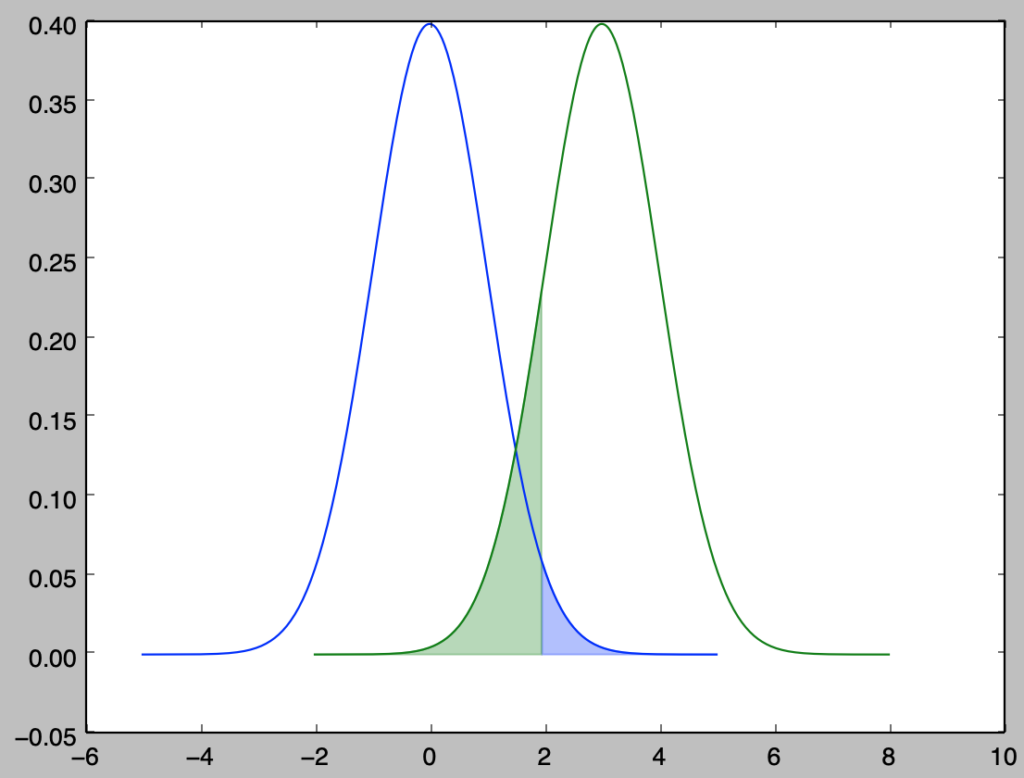
上記の青の積分の値が$\alpha/2 = 0.025$に対応し、緑の部分の積分の値が$\beta$に一致する。ここで$\alpha$が有意水準、$1-\beta$が検出力である。
サンプルサイズ設計
分散$\sigma^2$の$n$個のサンプルが得られたとき、帰無仮説$H_{0}$に対応する母平均を$\mu_{0}$、対立仮説$H_{1}$に対応する母平均を$\mu_{1}$とおき、有意水準を$\alpha$、検出力を$1-\beta$と定める。また標準正規分布$\mathcal{N}(0,1)$の上側$\alpha$%点、$\beta$%点をそれぞれ$z_{\alpha}$、$z_{\beta}$のように定める。
$$
\large
\begin{align}
z_{\alpha} + z_{\beta} &= \frac{\mu_{1}-\mu_{0}}{\displaystyle \sqrt{\frac{\sigma^2}{n}}} \quad (1) \\
(z_{\alpha} + z_{\beta})^2 &= \frac{n(\mu_{1}-\mu_{0})^2}{\sigma^2} \\
n &= \frac{(z_{\alpha} + z_{\beta})^2}{\displaystyle \left( \frac{\mu_{1}-\mu_{0}}{\sigma} \right)^{2} } = \frac{(z_{\alpha} + z_{\beta})^2}{\Delta^{2}} \quad (2)
\end{align}
$$
$(1)$式は前節の「検出力$1-\beta$」で取り扱った図と対応させて理解すると良い。また、ここで$\alpha$と右辺の値が定まれば$\beta$の値が一意に定まることに注意しておくと良く、このことは「有意水準を定めたのちに対応する検出力の計算を行う」という一連の流れに対応する。
一般的な統計的仮説検定では帰無仮説$H_0$に関して有意水準$\alpha$を定めたのちに対立仮説$H_1$に関する検出力$1-\beta$を計算することから、「有意水準を先に定める」都合上、検出力$1-\beta$を制御する場合は右辺の値を変えるにあたってサンプルサイズを変える必要が生じる。
具体的に理解するにあたって$\mu_{0}<\mu_{1}$の上側$2.5$%片側検定かつ検出力$1-\beta=0.8$を考える場合、$z_{\alpha=0.025}$、$z_{\beta=0.2}$に関して下記が成立する。
$$
\large
\begin{align}
z_{\alpha=0.025} + z_{\beta=0.2} &= \frac{\mu_{1}-\mu_{0}}{\displaystyle \sqrt{\frac{\sigma^2}{n}}} \\
1.96 + 0.84 &= \frac{\mu_{1}-\mu_{0}}{\displaystyle \sqrt{\frac{\sigma^2}{n}}}
\end{align}
$$
上記は「統計検定準$1$級対応 統計学実践ワークブック」の$(10.1)$式に対応する。また、以下では$(2)$式に基づいて、$\mu_{0}<\mu_{1}$の上側$2.5$%片側検定を考える際に検出力$1-\beta$とサンプルサイズ$n$がどのように対応するかに関してグラフの作成を行なった。
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
Delta = np.array([0.2, 0.3, 0.5, 1., 2.])
beta = np.arange(0.5, 1., 0.01)
z_alpha = stats.norm.ppf(1.-0.025)
z_beta = -stats.norm.ppf(1.-beta)
for i in range(Delta.shape[0]):
n = (z_alpha+z_beta)**2/Delta[i]**2
plt.plot(beta, n, label="Delta: {:.2f}".format(Delta[i]))
plt.legend(loc="upper left")
plt.show()・実行結果
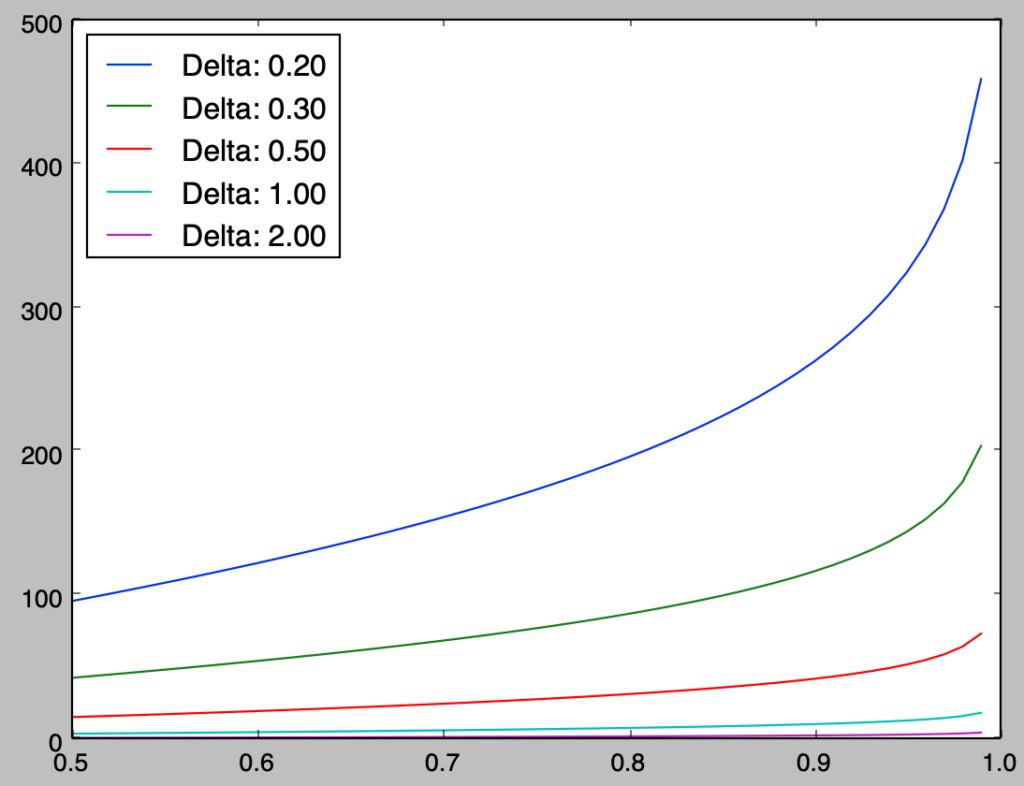
上記の実行結果より、検出力を大きくすると必要なサンプルサイズが大きくなることが確認できる。

[…] […]
[…] 有意水準$alpha$と検出力$1-beta$の値に基づくサンプルサイズ設計 […]
[…] 有意水準$alpha$と検出力$1-beta$の値に基づくサンプルサイズ設計 […]
[…] ・参考:有意水準$alpha$と検出力$1-beta$の値に基づくサンプルサイズ設計https://www.hello-statisticians.com/explain-terms-cat/sample_size1.html […]