「統計検定$2$級 公式問題集 CBT対応版」の解答例を取りまとめるにあたって、当記事では「PART.$2$ 分野・項目別 問題・解説」のCategory.$8$「検定」の解答例を作成しました。解答例は「統計の森」オリジナルのコンテンツであり、統計検定の公式とは一切関係ないことにご注意ください。
解答例
Q.1
ア)
検定統計量$Z$に関して$Z \sim \mathcal{N}(0,1)$が成立するので、有意水準$5$%の両側検定を考えると$|Z|>1.96$が棄却域となる。
イ)
検定統計量$T$に関して$T \sim t(20)$が成立するので、有意水準$5$%の両側検定を考えると$|T|>2.086$が棄却域となる。
ウ)
$T$に関して中心極限定理に基づく世紀近似を用いる場合の有意水準$5$%の両側検定の棄却域は$|T|>1.96$となる。
上記より、①が正解である。
Q.2
「第$1$種の過誤」は「帰無仮説$H_0$が正しいにも関わらず棄却すること」に該当するので、この問題では「$p=0.62$が正しいにも関わらず棄却すること」に対応する。よって①か②に絞られる。また、有意水準$\alpha$は棄却する確率に対応するので$0.62^3+0.38^3=0.2932$であり、②が正解である。
Q.3
検定統計量$T$の実現値を$t$とおくと、下記のように計算できる。
$$
\large
\begin{align}
t &= \frac{\bar{x}-\mu}{\hat{\sigma}/\sqrt{n}} \\
&= \frac{3.23 \times 2 \sqrt{6}}{8.72} \\
&= 1.81 \cdots
\end{align}
$$
自由度$n-1=23$の$t$分布$t(23)$の上側$\alpha’$点を$t_{\alpha=\alpha’}(23)$とおくとき、$t_{\alpha=0.01}(23)$〜$t_{\alpha=0.1}(23)$は下記のような値を持つ。
$$
\large
\begin{align}
t_{\alpha=0.01}(23) &= 2.500 \\
t_{\alpha=0.025}(23) &= 2.069 \\
t_{\alpha=0.05}(23) &= 1.714 \\
t_{\alpha=0.1}(23) &= 1.319
\end{align}
$$
$t_{\alpha=0.05}(23) < 1.81 < t_{\alpha=0.025}(23)$より、③が正解である。
Q.4
ア)
対立仮説が$H_1: \, p \neq p_0$であるので、両側検定を行う。
イ)
両側検定なので$|Z|>z_{\alpha=0.025}=1.96$が棄却域である。
ウ)
$|Z|>1.96$のとき棄却されるのは帰無仮説である。
よって、⑤が正解である。
Q.5
標本の不良品率を$\hat{r}$とおくとき、検定統計量$Z$と実現値$z$に関して下記が成り立つ。
$$
\large
\begin{align}
Z \sim \mathcal{N} \left( r, np(1-p) \right) \\
z &= \frac{\hat{r}-r}{\sqrt{p(1-p)/n}} \quad (1) \\
\hat{r} &= \frac{x}{n}
\end{align}
$$
上記の$(1)$式に$x=16, n=200, r=0.05$を代入すると下記が得られる。
$$
\large
\begin{align}
z &= \frac{\hat{r}-r}{\sqrt{p(1-p)/n}} \quad (1) \\
&= \frac{16/200-0.05}{\sqrt{0.05 \cdot 0.95 / 200}} \\
&= 1.946 \cdots
\end{align}
$$
$P$値は$P(Z \geq z)=P(Z \geq 1.95)=0.0256$が対応するので、正解は②である。
Q.6
セリーグの不偏標本分散を$\hat{\sigma}_{1}^{2}$、パリーグの不偏標本分散を$\hat{\sigma}_{2}^{2}$、共通の不偏標本分散を$\hat{\sigma}^{2}$とおくと、$\hat{\sigma}^{2}$は下記のように表される。
$$
\large
\begin{align}
\hat{\sigma}^{2} &= \frac{(m-1)\hat{\sigma}_{1}^{2} + (n-1)\hat{\sigma}_{2}^{2}}{m+n-2} \\
&= \frac{\sum(x_i-\bar{x})^2 + \sum(y_i-\bar{y})^2}{m+n-2}
\end{align}
$$
また、検定統計量の実現値を$t$とおくと、$t$は下記のように表される。
$$
\large
\begin{align}
t &= \frac{(\bar{x}-\bar{y}) – 0}{\displaystyle \sqrt{\frac{1}{m}+\frac{1}{n}} \hat{\sigma}} \\
&= \frac{\bar{x}-\bar{y}}{\displaystyle \sqrt{ \left( \frac{1}{m}+\frac{1}{n} \right) \frac{\sum(x_i-\bar{x})^2 + \sum(y_i-\bar{y})^2}{m+n-2}}}
\end{align}
$$
上記に$\displaystyle \sum(x_i-\bar{x})^2 = 13549, \sum(y_i-\bar{y})^2 = 7763, \bar{x}=233.7, \bar{y}=185.3, m=n=6$を代入すると下記のような計算結果が得られる。
$$
\large
\begin{align}
t &= \frac{\bar{x}-\bar{y}}{\displaystyle \sqrt{ \left( \frac{1}{m}+\frac{1}{n} \right) \frac{\sum(x_i-\bar{x})^2 + \sum(y_i-\bar{y})^2}{m+n-2}}} \\
&= \frac{233.7-185.3}{\displaystyle \sqrt{ \left( \frac{1}{6}+\frac{1}{6} \right) \frac{13549 + 7763}{6+6-2}}} \\
&= 1.815 \cdots
\end{align}
$$
上記より正解は④である。
Q.7
| No. | $1$ | $2$ | $3$ | $4$ | $5$ | $6$ | $7$ | $8$ | $9$ | $10$ | 平均 |
| 前 | $130$ | $118$ | $128$ | $135$ | $126$ | $120$ | $126$ | $140$ | $127$ | $130$ | $128.0$ |
| 後 | $135$ | $120$ | $132$ | $135$ | $129$ | $128$ | $135$ | $139$ | $135$ | $132$ | $132.0$ |
「対応のある場合」なので、前後の差を$X$と起き、$X$の母平均を$\mu$、母分散を$\sigma^2$と考え、$H_{0}: \, \mu=0$と$H_{1}: \, \mu>0$の片側検定を行う。よって自由度は$9$、$t_{\alpha=0.05}(9)=1.833$であるので①が正解である。
Q.8
標本の不良品の比率を$\hat{p}_A, \hat{p}_B$、母集団の不良品の比率を$p_A, p_B$、標本の抽出数を$n_A, n_B$とおく。このとき二項分布の正規近似より下記が成立する。
$$
\large
\begin{align}
\hat{p}_A-\hat{p}_B \sim \mathcal{N} \left( p_A-p_B, \frac{\hat{p}_A(1-\hat{p}_A)}{n_A}+\frac{\hat{p}_B(1-\hat{p}_B)}{n_B} \right)
\end{align}
$$
ここで帰無仮説$H_0: \, d = p_A-p_B = 0$に対する検定統計量の実現値を$z$とおくと、$z$は下記のように計算できる。
$$
\large
\begin{align}
z &= \frac{\hat{p}_A-\hat{p}_B}{\displaystyle \sqrt{\frac{\hat{p}_A(1-\hat{p}_A)}{n_A}+\frac{\hat{p}_B(1-\hat{p}_B)}{n_B}}} \\
&= -0.181 \cdots
\end{align}
$$
上記の計算にあたっては$\displaystyle \hat{p}_A=\frac{16}{200}, \hat{p}_B=\frac{17}{200}, n_A=n_B=200$を代入し、計算を行なった。ここで$P$値は$P(|Z| \geq |z|) = P(|Z| \geq 0.18)$に対応するので下記のように計算できる。
$$
\large
\begin{align}
P(|Z| \geq |z|) &= P(|Z| \geq 0.18) \\
&= 2 P(Z \geq 0.18) \\
& \simeq 2 \times 0.4286 = 0.8572
\end{align}
$$
以上より、正解は⑤である。
Q.9
$F$値は下記のように計算できる。
$$
\large
\begin{align}
F &= \frac{19.5^2}{14.5^2} \\
&= 1.808 \cdots
\end{align}
$$
ここで、$F_{\alpha=0.025}(20,40)=2.068$であり、$\displaystyle \frac{1}{F_{\alpha=0.025}(40,20)}=\frac{1}{2.287}$であるので下記が成立する。
$$
\large
\begin{align}
\frac{1}{F_{\alpha=0.025}(40,20)} = \frac{1}{2.287} < F < 2.068 = F_{\alpha=0.025}(20,40)
\end{align}
$$
よって帰無仮説の「クラス間の分散が等しい」は$5$%で棄却できない。
上記より、②が正解である。
Q.10
$\alpha$と$\beta$が閾値$x_0$の定め方によりトレードオフであることから①か②に絞られる。
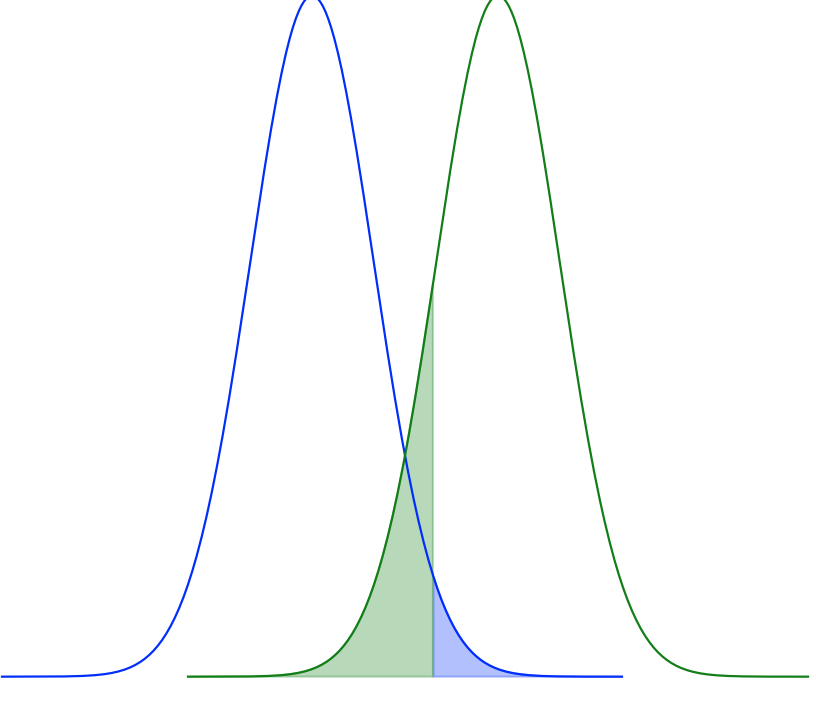
ここで$\alpha$は上図の青の面積、$\beta$が上図の緑の面積に対応する。上図より$\alpha+\beta$が閾値$x_0$の取り方により一定ではないことが確認できるので、②は不適切であり①が正解である。
・参考
有意水準や検出力に関しては抽象的で難しいので、下記で図を元に取りまとめました。
参考
・【統計検定$2$級対応】統計学入門まとめ
https://www.hello-statisticians.com/stat_basic
