数学検定準$1$級は数Ⅲまで相当の数学の基本トピックに関して取り扱った検定であり、統計学に必要な数学を身につける際の指標に役に立ちます。当記事では「日本数学検定協会 監修」の「数学検定問題集 準$1$級」より、第$3$章の「積分法とその応用」の解説と演習問題の解答例などを取り扱いました。
・数学検定まとめ
https://www.hello-statisticians.com/math_certificate
Contents
①不定積分、②不定積分の計算
計算技能問題
問題.$1$
$[1]$
$\displaystyle \frac{1}{\sqrt{x+5}+\sqrt{x}}$は下記のように変形を行うことができる。
$$
\large
\begin{align}
\frac{1}{\sqrt{x+5}+\sqrt{x}} &= \frac{\sqrt{x+5}-\sqrt{x}}{(\sqrt{x+5}+\sqrt{x})(\sqrt{x+5}-\sqrt{x})} \\
&= \frac{\sqrt{x+5}-\sqrt{x}}{x+5-x} \\
&= \frac{1}{5}(\sqrt{x+5}-\sqrt{x})
\end{align}
$$
よって不定積分は下記のように計算できる。
$$
\large
\begin{align}
\int \frac{1}{\sqrt{x+5}+\sqrt{x}} dx &= \frac{1}{5} \int (\sqrt{x+5}-\sqrt{x}) dx \\
&= \frac{1}{5} \left( \frac{2}{3}(x+5)^{\frac{3}{2}} + \frac{2}{3}x^{\frac{3}{2}} \right) + C \\
&= \frac{2}{15} \left( \sqrt{(x+5)^{3}} + \sqrt{x^{3}} \right) + C
\end{align}
$$
$[2]$
$$
\large
\begin{align}
\int \frac{x^2+3x+1}{\sqrt{x+1}} dx
\end{align}
$$
上記に対し、$t=\sqrt{x+1}$とおくと、$t^2=x+1$より$x=t^2-1$である。このとき$\displaystyle \frac{dx}{dt} = 2t$が成立する。よって不定積分は置換積分により下記のように得られる。
$$
\large
\begin{align}
\int \frac{x^2+3x+1}{\sqrt{x+1}} dx &= \int \frac{(t^2-1)^2+3(t^2-1)+1}{\cancel{t}} \cdot 2 \cancel{t} dt \\
&= 2 \int (t^4 – 2t^2 + 1 + 3t^2 – 3 + 1) dt \\
&= 2 \int (t^4 + t^2 – 1) dt \\
&= \frac{2}{5}t^5 + \frac{2}{3}t^3 – 2t + C \\
&= \frac{2}{5}(x+1)^2\sqrt{x+1} + \frac{2}{3}(x+1)\sqrt{x+1} – 2\sqrt{x+1} + C
\end{align}
$$
$[3]$
不定積分$\displaystyle \int \tan{x} dx$は下記のように計算できる。
$$
\large
\begin{align}
\int \tan{x} dx &= \int \frac{\sin{x}}{\cos{x}} dx \\
&= \int \frac{-(\cos{x})}{\cos{x}} dx \\
&= – \log{|\cos{x}|} + C
\end{align}
$$
$[4]$
$$
\large
\begin{align}
\int e^{\sqrt{x}} dx
\end{align}
$$
上記に対し$t=\sqrt{x}$とおくと、$t^2=x$より$x=t^2$である。このとき$\displaystyle \frac{dx}{dt} = 2t$が成立する。よって不定積分は置換積分により下記のように得られる。
$$
\large
\begin{align}
\int e^{\sqrt{x}} dx &= \int e^{t} \cdot 2t dt \\
&= 2t e^{t} – \int 2e^{t} dt \\
&= 2t e^{t} – 2e^{t} + C \\
&= 2\sqrt{x} e^{\sqrt{x}} – 2e^{\sqrt{x}} + C \\
&= 2(\sqrt{x}-1)e^{\sqrt{x}} + C
\end{align}
$$
$[5]$
部分積分を用いて下記のように計算できる。
$$
\large
\begin{align}
\int \frac{x}{\sin^{2}{x}} dx &= -\frac{x}{\tan{x}} + \int \frac{1}{\tan{x}} dx \\
&= -\frac{x}{\tan{x}} + \int \frac{(\sin{x})’}{\sin{x}} dx \\
&= -\frac{x}{\tan{x}} + \log{|\sin{x}|} + C
\end{align}
$$
$[6]$
部分分数分解を元に下記のように不定積分を計算できる。
$$
\large
\begin{align}
\int \frac{x}{x^2+2x+1} dx &= \int \frac{(x+1)-1}{(x+1)^2} dx \\
&= \int \frac{1}{x+1} dx – \int \frac{1}{(x+1)^2} dx \\
&= \log{|x+1|} + \frac{1}{x+1} + C
\end{align}
$$
$[7]$
部分分数分解を元に下記のように不定積分を計算できる。
$$
\large
\begin{align}
\int \frac{x}{x^2-x-2} dx &= \int \left( \frac{2}{3(x-2)} + \frac{1}{3(x+1)} \right) dx \\
&= \frac{2}{3} \log{|x-2|} + \frac{1}{3} \log{|x+1|} + C \\
&= \frac{1}{3} \log{(x-2)^2|x+1|} + C
\end{align}
$$
数理技能問題
問題.$1$
問題.$2$
$$
\large
\begin{align}
I_{n} = \int \frac{1}{\sqrt{(x^2+1)^{n}}} dx = \int (x^2+1)^{-\frac{n}{2}} dx
\end{align}
$$
$[1]$
$I_{n}$は部分積分法に基づいて下記のように変形できる。
$$
\large
\begin{align}
I_{n} &= \int (x^2+1)^{-\frac{n}{2}} dx \\
&= \int x’ (x^2+1)^{-\frac{n}{2}} dx \\
&= x (x^2+1)^{-\frac{n}{2}} – \int x \cdot -\frac{n}{2} \cdot (x^2+1)^{-\frac{n}{2}-1} \cdot (x^2+1)’ dx \\
&= x(x^2+1)^{-\frac{n}{2}} + \frac{n}{2} \int 2x^2(x^2+1)^{-\frac{n}{2}-1} dx \\
&= \frac{x}{\sqrt{(x^2+1)^{n}}} + n \int \frac{x^2}{\sqrt{(x^2+1)^{n+2}}} dx \\
&= \frac{x}{\sqrt{(x^2+1)^{n}}} + n \int \frac{x^2+1-1}{(x^2+1)\sqrt{(x^2+1)^{n}}} dx \\
&= \frac{x}{\sqrt{(x^2+1)^{n}}} + n \int \frac{1}{\sqrt{(x^2+1)^{n}}} dx – n \int \frac{1}{\sqrt{(x^2+1)^{n+2}}} dx \\
&= \frac{x}{\sqrt{(x^2+1)^{n}}} + n I_{n} – n I_{n+2} \quad (1)
\end{align}
$$
$(1)$式は下記のように変形できる。
$$
\large
\begin{align}
I_{n} &= \frac{x}{\sqrt{(x^2+1)^{n}}} + n I_{n} – n I_{n+2} \quad (1) \\
n I_{n+2} &= \frac{x}{\sqrt{(x^2+1)^{n}}} + (n-1) I_{n} \\
I_{n+2} &= \frac{x}{n \sqrt{(x^2+1)^{n}}} + \frac{n-1}{n} I_{n}
\end{align}
$$
$[2]$
$I_{3}$は下記のように得られる。
$$
\large
\begin{align}
I_{3} &= \frac{x}{\sqrt{(x^2+1)^{1}}} + \frac{0}{1} I_{1} + C \\
&= \frac{x}{\sqrt{x^2+1}} + C
\end{align}
$$
同様に$I_{5}$は下記のように得られる。
$$
\large
\begin{align}
I_{5} &= \frac{x}{3\sqrt{(x^2+1)^{3}}} + \frac{2}{3} I_{3} + C \\
&= \frac{x}{3\sqrt{(x^2+1)^{3}}} + \frac{2x}{3\sqrt{x^2+1}} + C_1
\end{align}
$$
③定積分、④定積分の計算
計算技能問題
問題.$1$
$[1]$
下記のように定積分の計算を行うことができる。
$$
\large
\begin{align}
\int_{0}^{1} \frac{e^{x}}{e^{x}+e^{-x}} dx &= \int_{0}^{1} \frac{e^{2x}}{e^{2x}+1} dx \\
&= \frac{1}{2} \int_{0}^{1} \frac{2e^{2x}}{e^{2x}+1} dx \\
&= \frac{1}{2} \int_{0}^{1} \frac{(e^{2x}+1)’}{e^{2x}+1} dx \\
&= \frac{1}{2} \left[ \log{|e^{2x}+1|} \right]_{0}^{1} \\
&= \frac{1}{2} (\log{(e^{2}+1)} – \log{2}) \\
&= \frac{1}{2} \log{ \frac{e^{2}+1}{2} }
\end{align}
$$
・別解
$t=e^x$とおいて、置換積分を考えても計算できる。問題集に置換積分を用いた解法があるので計算の詳細は省略する。
$[2]$
$x = \tan{\theta}$とおくと、$\cos^{2}{\theta}+\sin^{2}{x}=1$の両辺を$\cos^{2}{\theta}$で割ることで$\displaystyle \tan^{2}{\theta}+1=\frac{1}{\cos^2{\theta}}$が導出できる。
このとき$\displaystyle \frac{dx}{d \theta}$は下記のように表せる。
$$
\large
\begin{align}
\frac{dx}{d \theta} &= \left( \frac{\sin{\theta}}{\cos{\theta}} \right)’ \\
&= \frac{\cos^{2}{\theta}-(-\sin^{2}{\theta})}{\cos^{2}{\theta}} \\
&= \frac{1}{\cos^{2}{\theta}}
\end{align}
$$
また、$x$と$\theta$の範囲は下記のように対応する。
| $x$ | $1 \to \sqrt{3}$ |
| $\theta$ | $\displaystyle \frac{\pi}{4} \to \frac{\pi}{3}$ |
よって定積分の計算は下記のように行える。
$$
\large
\begin{align}
\int_{1}^{\sqrt{3}} \frac{1}{x^2+1} dx &= \int_{\frac{\pi}{4}}^{\frac{\pi}{3}} \frac{1}{\tan^{2}{\theta}+1} \cdot \frac{1}{\cos^{2}{\theta}} d \theta \\
&= \int_{\frac{\pi}{4}}^{\frac{\pi}{3}} \frac{\cancel{\cos^{2}{\theta}}}{\cancel{\cos^{2}{\theta}}} d \theta \\
&= \left[ \theta \right]_{\frac{\pi}{4}}^{\frac{\pi}{3}} \\
&= \frac{\pi}{3} – \frac{\pi}{4} \\
&= \frac{\pi}{12}
\end{align}
$$
$[3]$
$t=4-3x^2$とおくと、$\displaystyle \frac{dt}{dx}=-6x$より下記が成立する。
$$
\large
\begin{align}
dx = -\frac{1}{6x} dt
\end{align}
$$
このとき、$x$と$t$の範囲は下記のように対応する。
| $x$ | $0 \to 1$ |
| $t$ | $\displaystyle 4 \to 1$ |
また、$t=4-3x^2$より$x^2$は下記のように表せる。
$$
\large
\begin{align}
x^2 = \frac{1}{3}(4-t)
\end{align}
$$
よって定積分の計算は下記のように行える。
$$
\large
\begin{align}
\int_{0}^{1} x^{3} \sqrt{4-3x^2} dx &= \int_{4}^{1} \frac{1}{3}(4-t) \cancel{x} \sqrt{t} -\frac{1}{6\cancel{x}} dt \\
&= \int_{1}^{4} \frac{1}{18}(4-t)\sqrt{t} dt \\
&= \frac{1}{18} \int_{1}^{4} (4t^{\frac{1}{2}}-t^{\frac{3}{2}}) dt \\
&= \frac{1}{18} \left[ \frac{8}{3}t^{\frac{3}{2}} – \frac{2}{5}t^{\frac{5}{2}} \right]_{1}^{4} \\
&= \frac{1}{18} \left[ \left( \frac{2^6}{3} – \frac{2^6}{5} \right) – \left( \frac{8}{3} – \frac{2}{5} \right) \right] \\
&= \frac{1}{18} \cdot \frac{94}{15} = \frac{47}{135}
\end{align}
$$
$[4]$
$x=2\sin{\theta}$とおくと、下記が成立する。
$$
\large
\begin{align}
\frac{1}{\sqrt{4-x^2}} &= \frac{1}{\sqrt{4(1-\sin^{2}{\theta})}} \\
&= \frac{1}{\sqrt{4\cos^{2}{\theta}}} \\
&= \frac{1}{2\cos{\theta}}
\end{align}
$$
このとき$\displaystyle \frac{dx}{d \theta}$は下記のように表せる。
$$
\large
\begin{align}
\frac{dx}{d \theta} &= (2\sin{\theta})’ \\
&= 2 \cos{\theta}
\end{align}
$$
また、$x$と$\theta$の範囲は下記のように対応する。
| $x$ | $0 \to 1$ |
| $\theta$ | $\displaystyle 0 \to \frac{\pi}{6}$ |
よって定積分の計算は下記のように行える。
$$
\large
\begin{align}
\int_{0}^{1} \frac{1}{\sqrt{4-x^2}} dx &= \int_{0}^{\frac{\pi}{6}} \frac{1}{2 \cos{\theta}} \cdot 2 \cos{\theta} d \theta \\
&= \left[ \theta \right]_{0}^{\frac{\pi}{6}} \\
&= \frac{\pi}{6}
\end{align}
$$
$[5]$
$$
\large
\begin{align}
\int_{0}^{1} \sqrt{1+\sqrt{x}} dx
\end{align}
$$
上記に対し、$u = 1+\sqrt{x}$とおくと$x=(u-1)^2$である。このとき$\displaystyle \frac{dx}{du}$は下記のように表せる。
$$
\large
\begin{align}
\frac{dx}{du} = 2(u-1)
\end{align}
$$
また、$x$と$u$の範囲は下記のように対応する。
| $x$ | $0 \to 1$ |
| $u$ | $1 \to 2$ |
よって定積分の計算は下記のように行える。
$$
\large
\begin{align}
\int_{0}^{1} \sqrt{1+\sqrt{x}} dx &= \int_{1}^{2} \sqrt{u} \cdot 2(u-1) du \\
&= 2\int_{1}^{2} (u^{\frac{3}{2}} – u^{\frac{1}{2}}) du \\
&= 2 \left[ \frac{2}{5}u^{\frac{5}{2}} – \frac{2}{3}u^{\frac{3}{2}} \right]_{1}^{2} \\
&= 2 \left( \frac{2}{5}2^{\frac{5}{2}} – \frac{2}{3}2^{\frac{3}{2}} \right) – 2 \left( \frac{2}{5}1^{\frac{5}{2}} – \frac{2}{3}1^{\frac{3}{2}} \right) \\
&= 2 \left( \frac{8\sqrt{2}}{5} – \frac{4\sqrt{2}}{3} \right) – 2 \left( \frac{2}{5} – \frac{2}{3} \right) \\
&= \frac{8}{15}(\sqrt{2}+1)
\end{align}
$$
$[6]$
部分積分法を用いることで下記のように定積分の計算を行うことができる。
$$
\large
\begin{align}
\int_{1}^{e} x^{3} \log{x} dx &= \frac{1}{4} \left[ x^{4} \log{x} \right]_{1}^{e} – \frac{1}{4} \int_{1}^{e} x^{4} \cdot \frac{1}{x} dx \\
&= \frac{e^4}{4} – \frac{1}{16} \left[ x^{4} \right]_{1}^{e} \\
&= \frac{4e^4 – e^4 + 1}{16} = \frac{3e^4 + 1}{16}
\end{align}
$$
数理技能問題
問題.$1$
$[1]$
$$
\large
\begin{align}
\int_{0}^{\frac{\pi}{2}} \frac{\cos{x}}{8+\cos^{2}{x}} dx
\end{align}
$$
$u = \sin{x}$とおくと、下記が成立する。
$$
\large
\begin{align}
\frac{du}{dx} &= \cos{x} \\
\cos{x} dx &= du
\end{align}
$$
また、$x$と$u$の範囲は下記のように対応する。
| $x$ | $\displaystyle 0 \to \frac{\pi}{2}$ |
| $u$ | $0 \to 1$ |
よって定積分の計算は下記のように行える。
$$
\large
\begin{align}
\int_{0}^{\frac{\pi}{2}} \frac{\cos{x}}{8+\cos^{2}{x}} dx &= \int_{0}^{\frac{\pi}{2}} \frac{\cos{x}}{9-\sin^{2}{x}} dx \\
&= \int_{0}^{1} \frac{1}{9-u^2} du \\
&= \int_{0}^{1} \frac{1}{(3+u)(3-u)} du \\
&= \int_{0}^{1} \left( \frac{1}{3+u} + \frac{1}{3-u} \right) du \\
&= \left[ \log{(3+u)} – \log{(3-u)} \right]_{0}^{1} \\
&= (\log{4}-\log{2}) – (\cancel{\log{3}}-\cancel{\log{3}}) \\
&= \log{\frac{4}{2}} \\
&= \log{2}
\end{align}
$$
$[2]$
$$
\large
\begin{align}
\int_{0}^{1} \sin{(\pi \sqrt{x})} dx
\end{align}
$$
$u = \sqrt{x}$とおくと、$x=u^2$より下記が成立する。
$$
\large
\begin{align}
\frac{dx}{du} = 2u
\end{align}
$$
また、$x$と$u$の範囲は下記のように対応する。
| $x$ | $0 \to 1$ |
| $u$ | $0 \to 1$ |
よって定積分の計算は下記のように行える。
$$
\large
\begin{align}
\int_{0}^{1} \sin{(\pi \sqrt{x})} dx &= \int_{0}^{1} \sin{(\pi u)} \cdot 2u du \\
&= \int_{0}^{1} 2u \sin{(\pi u)} du \\
&= 2 \left[ -\frac{1}{\pi} u \cos{(\pi u)} \right]_{0}^{1} + \frac{2}{\pi} \int_{0}^{1} \cos{(\pi u)} du \\
&= -\frac{2}{\pi} \cos{\pi} + \frac{2}{\pi} \left[ \frac{1}{\pi} \sin{(\pi u)} \right]_{0}^{1} \\
&= \frac{2}{\pi}
\end{align}
$$
⑤定積分に関連した問題
計算技能問題
問題.$1$
問題.$2$
数理技能問題
問題.$1$
問題.$2$
⑥面積
計算技能問題
問題.$1$
面積は下記のように計算することができる。
$$
\large
\begin{align}
e^{2} – \int_{1}^{e^2} \frac{1}{2} \log{x} dx &= e^{2} – \frac{1}{2} \left[ x\log{x} \right]_{1}^{e^2} + \frac{1}{2} \int_{1}^{e^2} \cancel{x} \cdot \frac{1}{\cancel{x}} dx \\
&= e^{2} – \frac{1}{2} e^{2} \log{e^2} + \frac{1}{2} \left[ x \right]_{1}^{e^2} \\
&= \frac{1}{2}(e^2-1)
\end{align}
$$
数理技能問題
問題.$1$
$[1]$
$$
\large
\begin{align}
x &= t – \sin{t} \\
y &= 1 – \cos{t}
\end{align}
$$
$\displaystyle \frac{dx}{dt} = 1 – \cos{t} \geq 0$より、$x$は$t$について単調増加であり、$t$の値に応じて$x$は下記のように変化する。
| $t$ | $0 \to 2 \pi$ |
| $x$ | $0 \to 2 \pi$ |
ここで$y=1-\cos{t} \geq 0$が成立するので面積は下記のように計算することができる。
$$
\large
\begin{align}
\int_{0}^{2 \pi} |y| dx &= \int_{0}^{2 \pi} (1 – \cos{t}) \cdot (1 – \cos{t}) dt \\
&= \int_{0}^{2 \pi} (1 – \cos{t})^{2} dt \\
&= \int_{0}^{2 \pi} (1 – 2 \cos{t} + \cos^{2}{t}) dt \\
&= \int_{0}^{2 \pi} \left( 1 – 2 \cos{t} + \frac{\cos{2t}+1}{2} \right) dt \\
&= \int_{0}^{2 \pi} \left( \frac{1}{2} \cos{2t} – 2 \cos{t} + \frac{3}{2} \right) dt \\
&= \left[ \frac{1}{4} \sin{2t} – 2 \sin{t} + \frac{3}{2}t \right]_{0}^{2 \pi} \\
&= \frac{3}{2} \cdot 2 \pi \\
&= 3 \pi
\end{align}
$$
・考察
本問題のサイクロイドは下記を実行することでグラフを作成できる。
import numpy as np
import matplotlib.pyplot as plt
t = np.linspace(0, 6*np.pi, 150)
x = t - np.sin(t)
y = 1 - np.cos(t)
plt.plot(x,y)
plt.show()実行結果
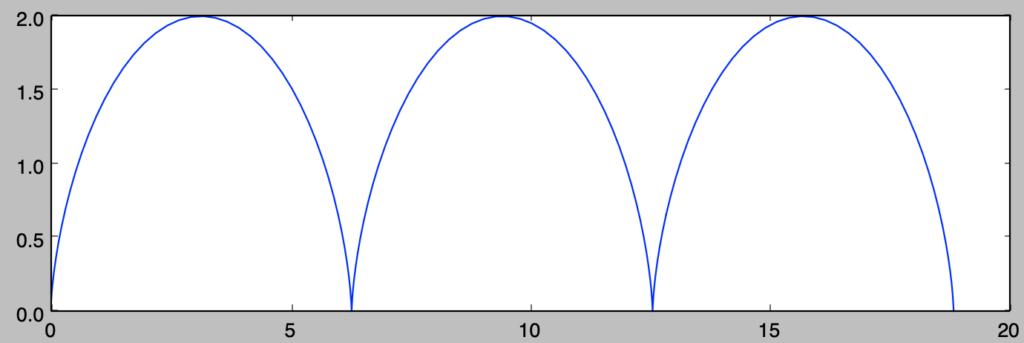
問題.$2$
⑦体積、⑧曲線の長さと道のり
計算技能問題
問題.$1$
体積$V$は下記のように計算できる。
$$
\large
\begin{align}
V &= 2 \pi \int_{0}^{1} (\sqrt{4-(x-2)^2})^2 dx \\
&= 2 \pi \int_{0}^{1} 4-(x-2)^2 dx \\
&= 2 \pi \left[ 4x – \frac{1}{3}(x-2)^3 \right]_{0}^{1} \\
&= 2 \pi \left[ \left( 4-\frac{(-1)^3}{3} \right) – \left( \frac{(-2)^3}{3} \right) \right] \\
&= 2 \pi \left[ 4 + \frac{1}{3} – \frac{8}{3} \right] \\
&= \frac{10}{3} \pi
\end{align}
$$
体積$W$は下記のように計算できる。
$$
\large
\begin{align}
W &= 2\pi \left[ \int_{0}^{\sqrt{3}} (\sqrt{4-y^2})^2 dy – \int_{0}^{\sqrt{3}} (2-\sqrt{4-y^2})^2 dy \right] \\
&= 2\pi \int_{0}^{\sqrt{3}} \left[ \cancel{(4-y^2)} – (4 + \cancel{(4-y^2)} – 4\sqrt{4-y^2}) \right] dy \\
&= 8\pi \int_{0}^{\sqrt{3}} (\sqrt{4-y^2} – 1) dy \quad (1)
\end{align}
$$
上記の$\displaystyle \int_{0}^{\sqrt{3}} \sqrt{4-y^2} dy$に対し、$x = 2 \sin{u}$とおくと$\displaystyle \frac{dx}{du} = 2\cos{u}$が成立する。また、$x$と$u$の範囲は下記のように対応する。
| $x$ | $0 \to \sqrt{3}$ |
| $u$ | $\displaystyle 0 \to \frac{\pi}{3}$ |
よって$\displaystyle \int_{0}^{\sqrt{3}} \sqrt{4-y^2} dy$は下記のように計算できる。
$$
\large
\begin{align}
\int_{0}^{\sqrt{3}} \sqrt{4-y^2} dy &= \int_{0}^{\frac{\pi}{3}} \sqrt{4-4\sin^2{u}} \cdot 2 \cos{u} du \\
&= \int_{0}^{\frac{\pi}{3}} \sqrt{4\cos^{2}{u}} \cdot 2 \cos{u} du \\
&= 2 \int_{0}^{\frac{\pi}{3}} 2 \cos^{2}{u} du \\
&= 2 \int_{0}^{\frac{\pi}{3}} (\cos{2u} + 1) du \\
&= \left[ \sin{2u} + 2u \right]_{0}^{\frac{\pi}{3}} \\
&= \sin{\frac{2\pi}{3}} + \frac{2}{3} \pi \\
&= \frac{2}{3} \pi + \frac{\sqrt{3}}{2}
\end{align}
$$
$(1)$式は下記のように計算できる。
$$
\large
\begin{align}
W &= 8\pi \int_{0}^{\sqrt{3}} (\sqrt{4-y^2} – 1) dy \quad (1) \\
&= 8\pi \left( \frac{2}{3} \pi + \frac{\sqrt{3}}{2} \right) – 8 \pi \left[ y \right]_{0}^{\sqrt{3}} \\
&= \frac{16}{3} \pi^2 + 4 \sqrt{3} \pi – 8 \sqrt{3} \pi \\
&= \frac{16}{3} \pi^2 – 4 \sqrt{3} \pi
\end{align}
$$
問題.$2$
$[1]$
下記のように計算できる。
$$
\large
\begin{align}
\int_{0}^{t} (4-2u) du &= \left[ 4u – u^2 \right]_{0}^{t} \\
&= 4t – t^2
\end{align}
$$
$[2]$
道のり$L$は下記のように計算できる。
・$t \leq 2$のとき
$$
\large
\begin{align}
L &= \int_{0}^{t} (4-2u) du \\
&= \left[ 4u – u^2 \right]_{0}^{t} \\
&= 4t – t^2
\end{align}
$$
・$2 < t$のとき
$$
\large
\begin{align}
L &= \int_{0}^{2} (4-2u) du + \int_{2}^{t} (2u-4) du \\
&= \left[ 4u – u^2 \right]_{0}^{2} + \left[ u^2-4u \right]_{2}^{t} \\
&= 8 – 4t + t^2
\end{align}
$$
数理技能問題
問題.$1$
体積$V$は下記のように計算できる。
$$
\large
\begin{align}
V &= \pi \int_{\frac{1}{3}\pi}^{\frac{2}{3}\pi} (\sin{x})^{2} dx + \pi \int_{\frac{2}{3}\pi}^{\pi} (\sin{2x})^{2} dx – \pi \int_{\frac{1}{3}\pi}^{\frac{1}{2}\pi} (\sin{2x})^{2} dx \\
&= \frac{\pi}{2} \int_{\frac{1}{3}\pi}^{\frac{2}{3}\pi} (1-\cos{2x}) dx + \frac{\pi}{2} \int_{\frac{2}{3}\pi}^{\pi} (1-\cos{4x}) dx – \frac{\pi}{2} \int_{\frac{1}{3}\pi}^{\frac{1}{2}\pi} (1-\cos{4x}) dx \\
&= \frac{\pi}{4} \left[ (2x-\sin{2x}) \right]_{\frac{1}{3}\pi}^{\frac{2}{3}\pi} + \frac{\pi}{8} \left[ 4x-\sin{4x} \right]_{\frac{2}{3}\pi}^{\pi} – \frac{\pi}{8} \left[ 4x-\sin{4x} \right]_{\frac{1}{3}\pi}^{\frac{1}{2}\pi} \\
&= \frac{\pi}{8} \left( \frac{4(2-1)}{3}\pi + \frac{4(3-2)}{3}\pi – \frac{4(3-2)}{6}\pi \right) \\
&+ \frac{\pi}{4} \left[ -\sin{\frac{4\pi}{3}} + \sin{\frac{2\pi}{3}} \right] + \frac{\pi}{8} \left[ -\sin{4\pi} + \sin{\frac{8\pi}{3}} \right] – \frac{\pi}{8} \left[ -\sin{2\pi} + \sin{\frac{4\pi}{3}} \right] \\
&= \frac{\pi}{8} \cdot \frac{6}{3} \pi + \frac{\pi}{4} \cdot \sqrt{3} + \frac{\pi}{8} \cdot \frac{\sqrt{3}}{2} + \frac{\pi}{8} \cdot \frac{\sqrt{3}}{2} \\
&= \frac{1}{4} \pi^{2} + \frac{3 \sqrt{3}}{8} \pi
\end{align}
$$
