数理統計学の検定論で出てくる検出力関数(power function)は一様最強力検定や一様最強力検定の理解にあたって重要な概念です。当記事では不偏検定の導入の際に用いられる正規分布の母平均の両側検定を行う際の検出力関数の描画を取り扱いました。
「数理統計学 統計的推論の基礎(共立出版)」の$10$章の「統計的仮説検定の考え方」の内容を主に参考に、作成を行いました。
・参考:有意水準$\alpha$と検出力$1-\beta$の値に基づくサンプルサイズ設計
https://www.hello-statisticians.com/explain-terms-cat/sample_size1.html
Contents
前提の確認
正規分布の確率密度関数
当記事では分散$1$の正規分布$\mathcal{N}(\mu,1)$に関して考察を行う。$\mathcal{N}(\mu,1)$の確率密度関数を$\phi(x; \mu)$とおくと、$\phi(x; \mu)$は下記のように表すことができる。
$$
\large
\begin{align}
\phi(x; \mu) = \frac{1}{\sqrt{2 \pi}} \exp{ \left[ -\frac{(x-\mu)^2}{2} \right] } \quad (1)
\end{align}
$$
また、上記の累積分布関数を$\Phi(x; \mu)$とおくと下記のように表せる。
$$
\large
\begin{align}
\Phi(x; \mu) = \int_{-\infty}^{x} \phi(u; \mu) du
\end{align}
$$
有意水準・検出力の定義と解釈
正規分布の母平均$\mu$に関する仮説検定を行うにあたって帰無仮説$H_0: \, \mu=\mu_0$、対立仮説$H_1: \, \mu=\mu_1$を定義する。このとき$\mu_0 < \mu_1$であれば下記のような図で仮説検定を表すことができる。
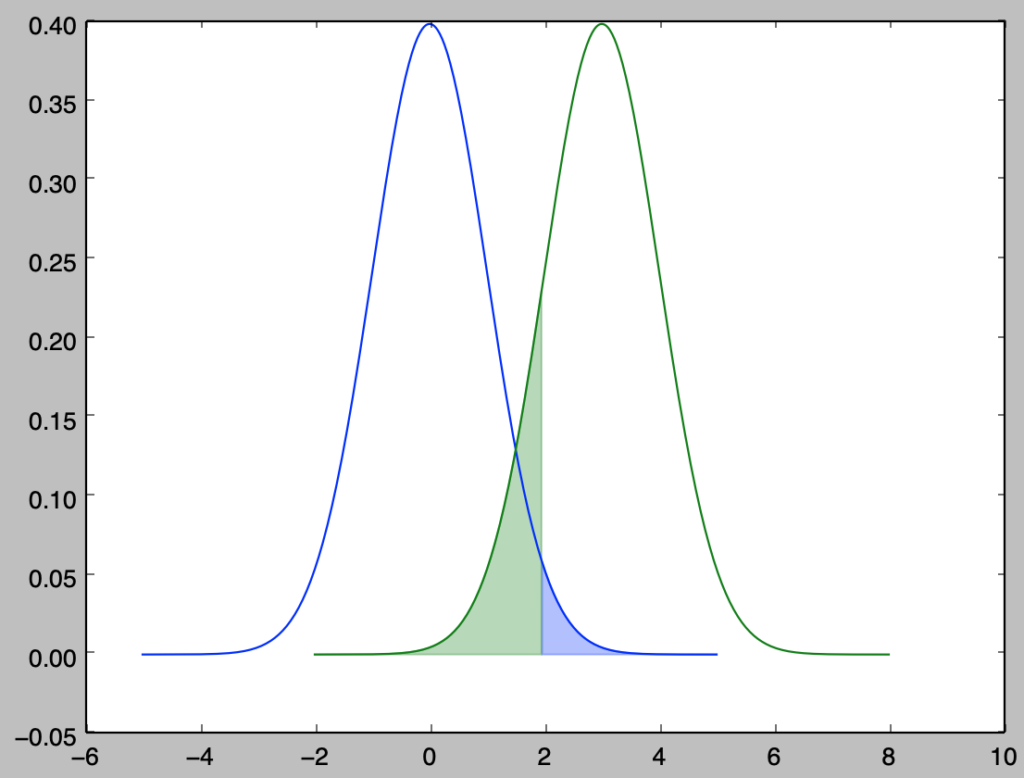
ここで上記の検定統計量$T(x)$に関して$T(x) \geq 1.96$を棄却域(rejection region)の$C$と定義する。このとき有意水準を$\alpha(C)$、検出力を$1-\beta(C)$とおくと、図の青色の領域と$\alpha(C)$、図の緑色の領域と$\beta(C)$がそれぞれ対応する。
また、前項で確認を行なった正規分布の確率密度関数を表す$(1)$式を元に有意水準$\alpha(C)$と検出力を$1-\beta(C)$はそれぞれ下記のような数式で表すことができる。
$$
\large
\begin{align}
\alpha(C) &= \int_{C} \phi(x; \mu_0) dx \\
1-\beta(C) &= \int_{C} \phi(x; \mu_1) dx
\end{align}
$$
数式の理解にあたっては$\phi(x; \mu_0)$が図の青色の曲線に対応し、$\phi(x; \mu_1)$が図の緑色の曲線に対応することに着目しておくと良い。
検出力と検出力関数
サンプルサイズ設計のような統計学の活用の際は検出力が主に用いられるが、数理統計学における検定論では検出力関数を元に考察を行うので抑えておくと良い。
検出力は対立仮説のパラメータの集合である$\Theta_1$を元に表されることが多い一方で、検出力関数は帰無仮説のパラメータの集合の$\Theta_0$の範囲を含む$\theta \in \Theta_0 \cup \Theta_1$で表すことが多いので注意が必要である。
$\theta \in \Theta_0 \cup \Theta_1$で表すのは片側検定の場合は$\theta \in \Theta_1$に対して一様最強力検定があるが、両側検定では不偏検定を用いるにあたって$\theta \in \Theta_0$の区間も合わせて図示を行う必要があるからではないかと推察される。
上記に基づいて正規分布における検出力関数$1-\beta(C,\mu)$を下記のように定義する。
$$
\large
\begin{align}
1-\beta(C,\mu) = \int_{C} \phi(x; \mu) dx
\end{align}
$$
片側検定の検出力関数
$$
\large
\begin{align}
H_0 &: \, \mu = 0 \\
H_1 &: \, \mu > 0
\end{align}
$$
上記のように定義を行なった両側検定の帰無仮説$H_0$と対立仮説$H_1$に対し、下記のような棄却域$C_1, C_2, C_3$を仮定する。
$$
\large
\begin{align}
C_1 &= \left\{ \bar{x}: \bar{x} > \frac{1.645}{\sqrt{n}} \right\} \\
C_2 &= \left\{ \bar{x}: \bar{x} > \frac{1.96}{\sqrt{n}} \right\} \\
C_3 &= \left\{ \bar{x}: \bar{x} > \frac{2.576}{\sqrt{n}} \right\}
\end{align}
$$
このとき棄却域$C_1, C_2$に対してそれぞれの検出力関数は母平均$\mu$に関して下記のように計算できる。
$$
\large
\begin{align}
1-\beta(C_1,\mu) &= \int_{C_1} f(x; \mu) dx \\
&= P(Z > 1.645 – \sqrt{n} \mu) \\
1-\beta(C_2,\mu) &= \int_{C_2} f(x; \mu) dx \\
&= P(Z > 1.96 – \sqrt{n} \mu) \\
1-\beta(C_3,\mu) &= \int_{C_3} f(x; \mu) dx \\
&= P(Z > 2.576 – \sqrt{n} \mu)
\end{align}
$$
上記は$\mu$の関数であるので、次節で$\mu$の値に対応する検出力$1-\beta(C_1), 1-\beta(C_2), 1-\beta(C_3)$のグラフの描画を行う。
両側検定の検出力関数
$$
\large
\begin{align}
H_0 &: \, \mu = 0 \\
H_1 &: \, \mu \neq 0
\end{align}
$$
上記のように定義を行なった両側検定の帰無仮説$H_0$と対立仮説$H_1$に対し、下記のような棄却域$C_1, C_2, C_3$を仮定する。
$$
\large
\begin{align}
C_1 &= \left\{ \bar{x}: \bar{x} > \frac{1.645}{\sqrt{n}} \right\} \\
C_2 &= \left\{ \bar{x}: \bar{x} < -\frac{1.645}{\sqrt{n}} \right\} \\
C_3 &= \left\{ \bar{x}: |\bar{x}| > \frac{1.96}{\sqrt{n}} \right\}
\end{align}
$$
このとき棄却域$C_1, C_2, C_3$に対してそれぞれの検出力関数は母平均$\mu$に関して下記のように計算できる。
$$
\large
\begin{align}
1-\beta(C_1,\mu) &= \int_{C_1} f(x; \mu) dx \\
&= P(Z > 1.645 – \sqrt{n} \mu) \\
1-\beta(C_2,\mu) &= \int_{C_2} f(x; \mu) dx \\
&= P(Z < -1.645 – \sqrt{n} \mu) \\
1-\beta(C_3,\mu) &= \int_{C_3} f(x; \mu) dx \\
&= P(Z > 1.96 – \sqrt{n} \mu) + P(Z < -1.96 – \sqrt{n} \mu)
\end{align}
$$
上記は$\mu$の関数であるので、次節で$\mu$の値に対応する検出力$1-\beta(C_1), 1-\beta(C_2), 1-\beta(C_3)$のグラフの描画を行う。
検出力関数の描画
片側検定
$$
\large
\begin{align}
1-\beta(C_1,\mu) &= P(Z > 1.645 – \sqrt{n} \mu) \\
1-\beta(C_2,\mu) &= P(Z > 1.96 – \sqrt{n} \mu) \\
1-\beta(C_3,\mu) &= P(Z > 2.576 – \sqrt{n} \mu)
\end{align}
$$
ここで$n=1$の場合を考えると下記が得られる。
$$
\large
\begin{align}
1-\beta(C_1,\mu) &= P(Z > 1.645 – \mu) \\
1-\beta(C_2,\mu) &= P(Z > 1.96 – \mu) \\
1-\beta(C_3,\mu) &= P(Z > 2.576 – \mu)
\end{align}
$$
上記に基づいて下記を実行することでグラフの描画を行うことができる。
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
mu = np.arange(-5., 5.01, 0.01)
f_1 = 1. - stats.norm.cdf(1.645-mu)
f_2 = 1. - stats.norm.cdf(1.96-mu)
f_3 = 1. - stats.norm.cdf(2.576-mu)
plt.plot(mu, f_1, label="C_1")
plt.plot(mu, f_2, label="C_2")
plt.plot(mu, f_3, label="C_3")
plt.legend(loc="upper left")
plt.show()・実行結果
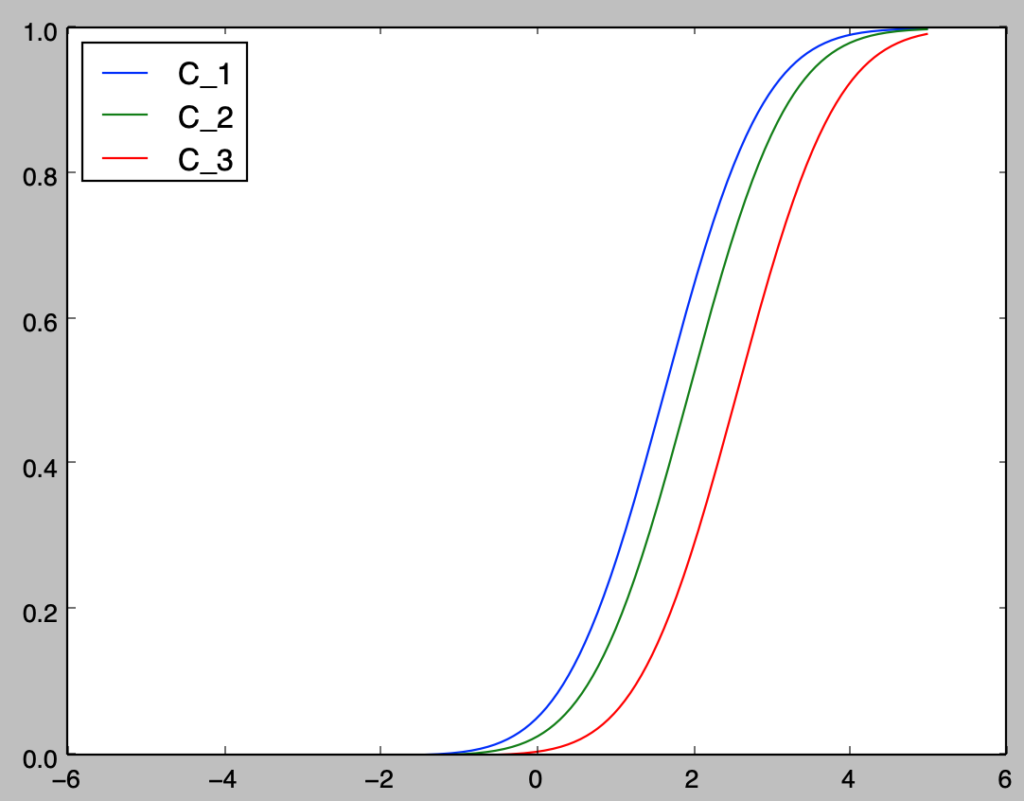
ここで検出力関数は$C_1, C_2, C_3$の順に大きいが、$C_1, C_2, C_3$はそれぞれ$\alpha=0.05, 0.025, 0.005$に対応しており、それぞれの有意水準$\alpha$の値で一様最強力であることが確認できる。
また、片側検定では$\mu_0 < \mu_1$などを仮定することから、$\mu > \mu_0$と表すこともできる。一方で検出力関数の理解しやすさの観点から当記事では両側検定と同様な定義を用いた。
両側検定
$$
\large
\begin{align}
1-\beta(C_1,\mu) &= P(Z > 1.645 – \sqrt{n} \mu) \\
1-\beta(C_2,\mu) &= P(Z < -1.645 – \sqrt{n} \mu) \\
1-\beta(C_3,\mu) &= P(Z > 1.96 – \sqrt{n} \mu) + P(Z < -1.96 – \sqrt{n} \mu)
\end{align}
$$
ここで$n=1$の場合を考えると下記が得られる。
$$
\large
\begin{align}
1-\beta(C_1,\mu) &= P(Z > 1.645 – \mu) \\
1-\beta(C_2,\mu) &= P(Z < -1.645 – \mu) \\
1-\beta(C_3,\mu) &= P(Z > 1.96 – \mu) + P(Z < -1.96 – \mu)
\end{align}
$$
上記に基づいて下記を実行することでグラフの描画を行うことができる。
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
mu = np.arange(-5., 5.01, 0.01)
f_1 = 1.-stats.norm.cdf(1.645-mu)
f_2 = stats.norm.cdf(-1.645-mu)
f_3 = 1. - stats.norm.cdf(1.96-mu) + stats.norm.cdf(-1.96-mu)
plt.plot(mu, f_1, label="C_1")
plt.plot(mu, f_2, label="C_2")
plt.plot(mu, f_3, label="C_3")
plt.legend()
plt.show()・実行結果
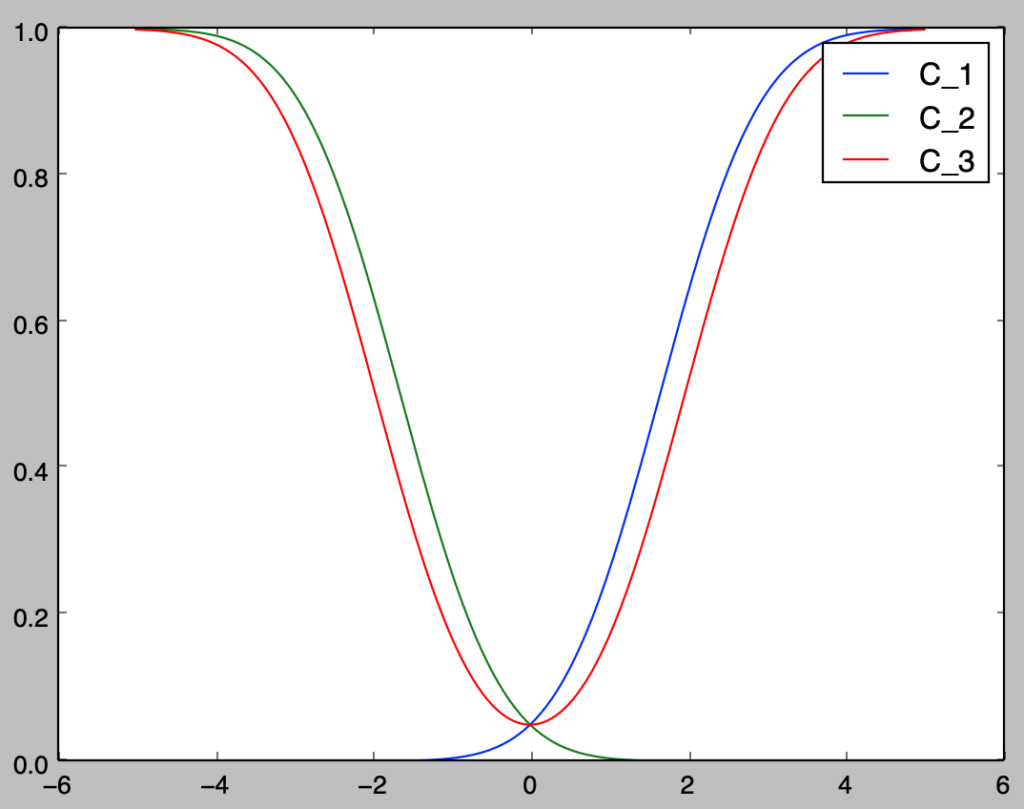
上図は「数理統計学 統計的推論の基礎(共立出版)」の図$10.4$と同様の図であることが確認できる。グラフより棄却域$C_3$は一様最強力検定ではないが、全区間で$\alpha=0.05$を上回る検出力を持つ不偏検定に限れば一様最強力である。このような検定を一様最強力不偏検定という。

[…] ・参考:正規分布の母平均の片側検定・両側検定における検出力関数の描画https://www.hello-statisticians.com/explain-terms-cat/power_function1.html […]