点群(point clouds)のような集合の入力(input set)の処理にあたってTransformerを用いた研究にSet Transformerがあります。当記事ではISAB(Induced Set Attention Block)などを中心にSet Transformer論文の取りまとめを行いました。
「Set Transformer: A Framework for Attention-based Permutation-Invariant Neural Networks」や「深層学習 改定第$2$版」の第$7$章「集合・グラフのためのネットワークと注意機構」の内容を参考に作成を行いました。
・用語/公式解説
https://www.hello-statisticians.com/explain-terms
Contents
前提の確認
Transformerの概要
Dot Product Attentionに主に基づくTransformerの仕組みについては既知である前提で当記事はまとめました。下記などに解説コンテンツを作成しましたので、合わせて参照ください。
・直感的に理解するTransformerの仕組み(統計の森作成)
Transformerの基本式
Transformerの基本的な処理であるDot Product Attentionを$\mathrm{Attention}(Q, K, V)$とおくと、$\mathrm{Attention}(Q, K, V)$は下記のような式で表されます。
$$
\large
\begin{align}
\mathrm{Attention}(Q, K, V) &= \mathrm{Softmax} \left( \frac{Q K^{\mathrm{T}}}{\sqrt{d}} \right) V \quad (1) \\
Q & \in \mathbb{R}^{m \times d}, K \in \mathbb{R}^{n \times d}, \, V \in \mathbb{R}^{n \times d} \\
Q K^{\mathrm{T}} & \in \mathbb{R}^{m \times n}, \, \mathrm{Attention}(Q, K, V) \in \mathbb{R}^{m \times d}
\end{align}
$$
Transformerでは基本的に$K=V$であり、さらにEncoderなどのSelf Attentionでは$Q=K=V$である場合が多いです。上記では$Q \neq K, \, K = V$の場合の立式を行いました。計算結果の$\mathrm{Attention}(Q, K, V)$が$\mathrm{Attention}(Q, K, V) \in \mathbb{R}^{m \times d}$のように$K, V$ではなく$Q$と同じサイズの行列が得られることに注意が必要です。また、$(1)$式における$\sqrt{d}$は$\mathrm{Softmax}$の計算結果が極端にならないように導入されます。
次に、Multi Head Attention演算を$\mathrm{Multihead}(Q, K, V)$のようにおくと、$\mathrm{Multihead}(Q, K, V)$は$(1)$式を元に下記のように定義されます。
$$
\large
\begin{align}
\mathrm{Multihead}(Q, K, V) &= \mathrm{concat}(O_1, \cdots , O_h)W^{O} \\
O_i &= \mathrm{Attention}(QW_{i}^{Q}, KW_{i}^{K}, VW_{i}^{V}) \\
O_i & \in \mathbb{R}^{m \times d_v}, \, \mathrm{concat}(O_1, \cdots , O_h) \in \mathbb{R}^{m \times h d_v} \\
W_{i}^{Q} & \in \mathbb{R}^{d \times d_k}, \, W_{i}^{K} \in \mathbb{R}^{d \times d_k}, W_{i}^{K} \in \mathbb{R}^{d \times d_v} \\
W^{O} & \in \mathbb{R}^{h d_v \times d} \\
d &= h d_{k} = h d_{v} \\
\mathrm{Multihead}(Q, K, V) & \in \mathbb{R}^{m \times d}
\end{align}
$$
Set Transformer
Multihead Attention Block
Set Transformerの論文ではMulti Head Attentionが下記のような$\mathrm{MAB}(X, Y)$で定義されます。
$$
\large
\begin{align}
\mathrm{MAB}(X, Y) &= \mathrm{LayerNorm}(H + \mathrm{FFN}(H)) \\
H &= \mathrm{LayerNorm}(X + \mathrm{Multihead}(X, Y, Y)) \\
X \in \mathbb{R}^{m \times d}, \, Y & \in \mathbb{R}^{n \times d}, H \in \mathbb{R}^{m \times d}, \, \mathrm{FFN}(H) \in \mathbb{R}^{m \times d}, \, \mathrm{MAB}(X, Y) \in \mathbb{R}^{m \times d}
\end{align}
$$
$\mathrm{MAB}(X, Y)$の$\mathrm{MAB}$はMultihead Attention Blockの略です。Set Transformerの論文では$\mathrm{MAB}(X, Y)$が下図のようにも表されます。
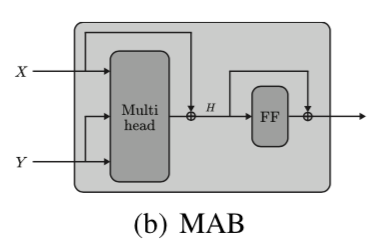
Multihead Attention Blockの理解にあたっては、出力の$\mathrm{MAB}(X, Y)$の行列のサイズが$X$の行列のサイズに一致することに注意しておくと良いです。$X$は通常のTransformerの$Q, K, V$の$Q$に対応します。
Set Attention Block
Set Transformerの論文ではSet Attention Blockの$\mathrm{SAB}(X)$を下記のように定義します。
$$
\large
\begin{align}
\mathrm{SAB} = \mathrm{MAB}(X, X)
\end{align}
$$
上記の式はSet Transformerの論文では下記のように図式化されます。
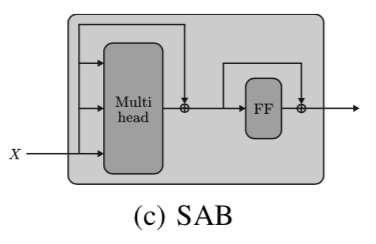
$\mathrm{SAB}(X)$はTransformerのEncoderにおける$Q=K=V$のSelf Attentionと同様の処理であると理解すると良いです。
Induced Set Attention Block
Set Transformerの論文ではInduced Set Attention Blockを表す$\mathrm{ISAB}_{m}(X)$が下記のように定義されます。
$$
\large
\begin{align}
\mathrm{ISAB}_{m}(X) &= \mathrm{MAB}(X, H) \\
H &= \mathrm{MAB}(I, X) \\
X & \in \mathbb{R}^{n \times d}, \, I \in \mathbb{R}^{m \times d}, \, H \in \mathbb{R}^{m \times d}, \, \mathrm{ISAB}_{m}(X) \in \mathbb{R}^{n \times d}
\end{align}
$$
上記の式はSet Transformerの論文では下記のように図式化されます。
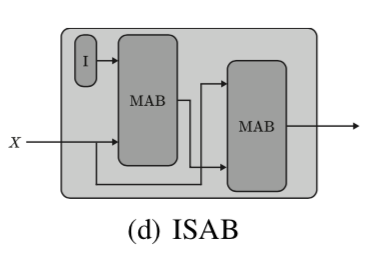
ISABの式は、「通常のTransformerにおけるAttentionの計算量が$\mathcal{O}(n^{2})$であり、点が多くなると処理が難しい」ので、「計算量が$\mathcal{O}(mn)$になるように$m$個のinducing pointsを導入しベクトル表現を$I \in \mathbb{R}^{m \times d}$のように定義した」と解釈すると良いです。また、ここで$\mathrm{MAB}$の演算を二回繰り返すことで、$\mathbb{R}^{n \times d} \longrightarrow \mathbb{R}^{m \times d} \longrightarrow \mathbb{R}^{n \times d}$のように元の$X$と同じ行列のサイズに戻すことができることも合わせて抑えておくと良いです。
ここで導入した$I \in \mathbb{R}^{m \times d}$はSet Transformerのパラメータ(trainable parameters)であり、Multi Head Attentionの写像計算のパラメータやFFNのMLP処理のパラメータと同様にTransformerの学習の際に値の推定が行われます。
Pooling
点群のように点の集合のPooling処理を取り扱う際に「CNNのような局所的なPoolingを行うことができない」点について注意が必要です。よって、点の集合のPoolingにあたっては全ての点の「平均」や「最大値」を計算することが一般的です。
一方で、Set TransformerではMultihead Attentionを用いたPooling(PMA; Pooling by Multihead Attention)が行われます。
Set Transformer論文ではPoolingによって$n$個の点を$k$個に集約する場合、下記のようなMultihead Attentionの処理が実行されます。
$$
\large
\begin{align}
\mathrm{PMA}_{k}(Z) &= \mathrm{MAB}(S, FFN(Z)) \\
S & \in \mathbb{R}^{k \times d}, \, Z \in \mathbb{R}^{n \times d}
\end{align}
$$
上記の$Z$は$X$の処理結果に対応し、$S$は前項の$I$のようにSet Transformerにおける学習パラメータです。
多くの場合は$k=1$が用いられる一方で、クラスタリング(clustering)のようなタスクの場合は$k > 1$が用いられることも合わせて抑えておくと良いです。$k=1$の場合は下記で取り扱ったグラフ分類と概ね同様なイメージで理解すると良いと思います。
Overall Architecture
SABを用いる場合
Set Attention Blockを用いる場合のEncoderとDecoderの計算例は複数のSABなどを用いて下記のように表されます。
$$
\large
\begin{align}
\mathrm{Encoder}(X) &= \mathrm{SAB}(\mathrm{SAB}(X)) = Z \\
\mathrm{Decoder}(Z) &= FFN(\mathrm{SAB}(\mathrm{PMA}_{k}(Z))) \\
X & \in \mathbb{R}^{n \times d}, Z \in \mathbb{R}^{n \times d}, \, \mathrm{Decoder}(Z) \in \mathbb{R}^{k \times d}
\end{align}
$$
ISABを用いる場合
EncoderにInduced Set Attention Blockを用いる場合もSet Attention Blockを用いる場合と同様に複数の$\mathrm{ISAB}_{m}$を用いて下記のように計算例が定義されます。
$$
\large
\begin{align}
\mathrm{Encoder}(X) &= \mathrm{ISAB}_{m}(\mathrm{ISAB}_{m}(X)) = Z \\
X & \in \mathbb{R}^{n \times d}, Z \in \mathbb{R}^{n \times d}
\end{align}
$$
Positional Encoding
Set Transformerでは基本的に前節で取り扱ったTransformerのアーキテクチャを用いる一方で、Positional Encodingは用いないことに注意が必要です。点群のような集合は入力間に順序がない(permutation invariant)ので、位置をEncodingするPositional Encodingの必要がありません。
むしろ「元々のTransformerには位置の情報がない一方で機械翻訳などのNLPタスクでは順序を取り扱う必要がありPositional Encodingが導入された」ので、Transformerのアルゴリズム自体は点群のような集合の取り扱いにより即していると解釈することもできると思います。
参考
・Transformer論文:Attention is All you need[2017]
・Set Transformer論文

[…] ISAB(Induced Set Attention Block)とSet Transformer […]