グラフニューラルネットワーク(GNN)が取り上げられることはそれほど多くはない一方で、Transformerを理解するにあたってはGNNを理解しておくことで直感的な理解が可能になります。当記事ではGNNの基本的な内容について把握できるように入門にあたって抑えておくべき事項をまとめました。
・Transformerの直感的理解
https://www.hello-statisticians.com/ml/deeplearning/transformer1.html
Contents
前提知識
Transformerとグラフニューラルネットワーク
下記で詳しく取り扱いました。当記事は下記の副読的な内容になるように取りまとめました。
「Transformer=グラフニューラルネットワーク+ネットワーク分析」と大まかに解釈できるので、当記事ではグラフニューラルネットワークについて詳しく取り扱います。
集合と要素
グラフ理論では基本的に数ⅠAの「集合」で取り扱われる内容を元に立式されます。当項では「集合」の基本的な式表記の確認を行います。たとえばサイコロの出目の$1$〜$6$の集合を$X$とおくとき$X$は下記のように定義できます。
$$
\large
\begin{align}
X = \{ 1, 2, 3, 4, 5, 6 \}
\end{align}
$$
このとき$X$の要素を$x$とおくと、$x \in X$のように表すことができます。$x \in X$は$x$が$1$〜$6$の要素を取りうることを表しており、「$1 \in X$」〜「$6 \in X$」も同義です。
「集合」については下記でも詳しくまとめましたので合わせて参照ください。
グラフ理論の式定義
グラフ理論の基本要素であるノード、エッジ、隣接行列の概要は上記で取り扱いましたので省略します。基本的には「点と線で物事の関連性を表す」と認識できれば十分です。当項では以下、グラフ理論やグラフニューラルネットワークを取り扱う際に用いられる数式について確認を行います。
グラフをGraphの$G$、ノードの集合を頂点を表すVerticeやVertexの$V$、エッジの集合をEdgeの$E$で定義すると、下記のような等式で表すことができます。
$$
\large
\begin{align}
G = (V,E) \quad (1)
\end{align}
$$
上記の式は論文などのフォーマルな議論ではよく用いられますがグラフ理論を学んだことがないと抽象的で理解しにくいので、具体例に基づいて確認します。
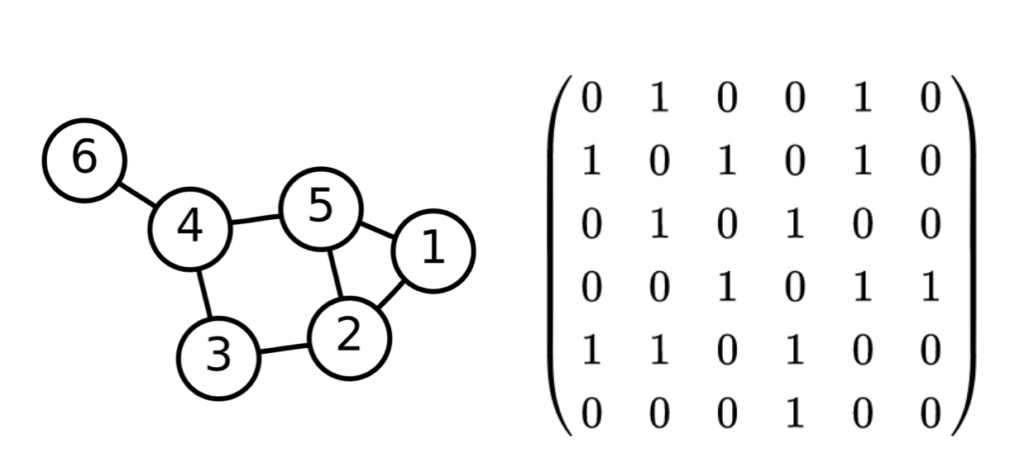
上図は「Transformerの解説」で用いたグラフの例ですが、上図を元に$(1)$式を具体的に確認します。図では$1$〜$6$のノードがあるので、ノードは$1$〜$6$の集合に対応します。よって、ノードの集合$V$は下記のように表されます。
$$
\large
\begin{align}
V = \{ 1, 2, 3, 4, 5, 6 \}
\end{align}
$$
また、グラフでは$1$と$2,5$、$2$と$1,3,5$、$3$と$2,4$、$4$と$3,5,6$、$5$と$1,2,4$、$6$と$4$がそれぞれ連結していることが確認できます。よって、エッジの集合$E$は下記のように表すことができます。
$$
\large
\begin{align}
E = \{ (1,2), (1,5), &(2,1), (2,3), (2,5), (3,2), (3,4), (4,3), (4,5), (4,6), \\
& (5,1), (5,2), (5,4), (6,4) \} \quad (2)
\end{align}
$$
上記では有向グラフの取り扱いに基づいて$(1,2)$と$(2,1)$を区別しましたが、無向グラフであることを前提に表記する場合は「左<右」を前提とできるので、下記のように表すことができます。
$$
\large
\begin{align}
E = { (1,2), (1,5), (2,3), (2,5), (3,4), (4,5), (4,6) } \quad (3)
\end{align}
$$
$(2)$と$(3)$を確認すると、$(3)$の要素のエッジの数は$7$個であり、$14$個である$(2)$のちょうど半分であることが確認できます。このことは「向きを考慮しない場合はエッジの数が半分になる」と解釈すれば良いです。
有向グラフを用いるか無向グラフを用いるかについては、グラフニューラルネットワークを取り扱う場合はそれぞれのノード単位で処理が行われるので、有向グラフを前提にすると考えやすいのではないかと思います。
グラフニューラルネットワークで必要な数式
前項ではグラフ理論におけるノード$V$とエッジ$E$の定義について確認を行いました。当項では前項の内容に加えてグラフニューラルネットワークで必要になる式定義を確認します。文字の選定は「A Comprehensive Survey on Graph Neural Networks」を参考に行いました。
ノードの特徴量
グラフニューラルネットワークではノードやエッジ単位に特徴量・隠れ層を割り当てます。ノード単位で計算を行うことが理解しやすいかつ多いので、当項では$n$個のノードに$d$次元の特徴量を割り当てる前提で式の確認を行います。
$$
\large
\begin{align}
X \in \mathbb{R}^{n \times d}
\end{align}
$$
上記の数式は一見難しいですが、「それぞれの要素が実数である$n$行$d$列の行列$X$を定義する」という意味合いであり、単に略記であると理解しておけば良いです。$n$個のノードへの$d$次元のベクトルの割り当ては、図で表すと下記のように表すことができます。
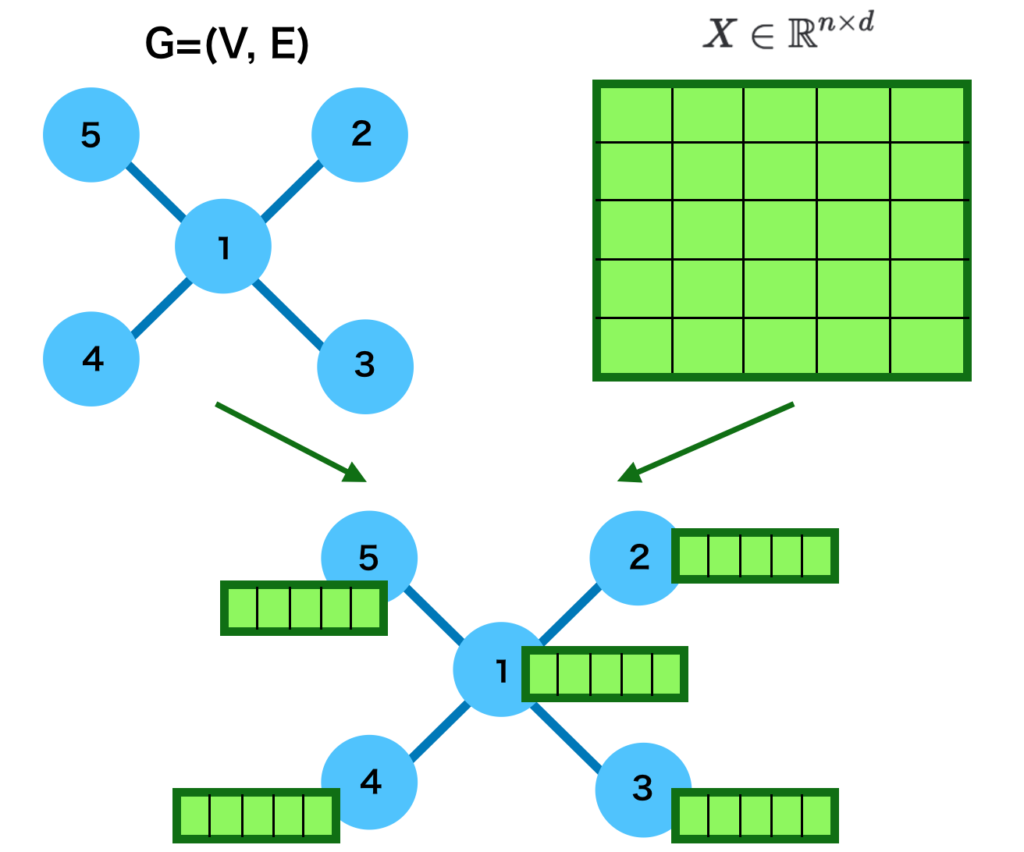
上図では$n=5, d=5$でノードに特徴量を割り当てた場合の図示を行いました。ここで各ノードに割り当てられたベクトルを$\vec{x}_{v}, \, v \in V$、グラフニューラルネットワークにおける$l$層目のグラフにおける隠れ層を$h_{v}^{l}$とおき、$h_{v}^{0} = \vec{x}_v$が成立すると仮定します。
このとき、$h_{v}^{0}$に対し、$L$層の処理を行うと$h_{v}^{L}$が得られますが、$h_{1}^{L}, \cdots , h_{n}^{L}$に基づきノードの分類やグラフの分類などを行うことができます。$h_{v}^{0}$から$h_{v}^{L}$を得る際の処理は次節で確認します。
ノードの集合・要素と$\displaystyle \sum$
$\displaystyle \sum$は$\displaystyle \sum_{i=1}^{n} x_1 = x_1 + \cdots + c_n$のような用いられ方をすることが多い一方で、集合や要素の表記に基づいて$\displaystyle \sum$が用いられることもあるので注意が必要です。
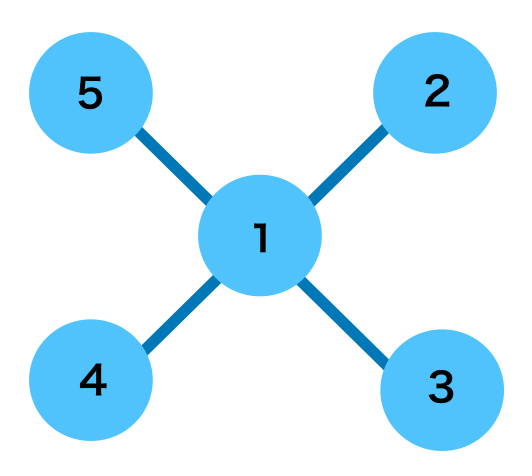
例えば上記のようなグラフに対し、$l$層におけるノード$1$に隣接するノードの隠れ層の和は下記のように表すことができます。
$$
\large
\begin{align}
\sum_{w \in N(1)} h_{w}^{l} = h_{2}^{l} + h_{3}^{l} + h_{4}^{l} + h_{5}^{l}
\end{align}
$$
このような式表記は一見難しく見えますが、グラフにおける特定のノードに隣接するノードの集合のようにインデックスが不規則になる場合の和の計算などの際に有用かつよく用いられるので、抑えておくと良いと思います。
ネットワーク分析
単語のベクトル表現に基づいてベクトル類似度を計算し、この値に基づいてグラフを描くことが可能です。この一連の流れは「ネットワーク分析」などのようにいわれますが、詳しくは下記で取り扱いました。
グラフニューラルネットワーク
MPNNフレームワーク
グラフニューラルネットワークの数式表記に関しては様々なものがありますが、MPNN(Message Passing Neural Network)の定義を元に考えると理解しやすいと思います。よって、当記事ではMPNN論文の数式を元にグラフニューラルネットワークの数式を定義し解釈を確認します。
グラフニューラルネットワークの基本式
$$
\large
\begin{align}
m_{v}^{l+1} &= \sum_{w \in N(v)} M_{l}(h_{v}^{l}, h_{w}^{l}, e_{vw}) \quad (4) \\
h_{v}^{l+1} &= U_{l}(h_{v}^{l}, m_{v}^{l+1}) \quad (5) \\
v & \in V
\end{align}
$$
上記の式はMPNN(Message Passing Neural Network)論文の$(1), (2)$式の$t$を$l$に置き換えて表しましたが、グラフニューラルネットワークの内部処理は上記を元に概ね理解することが可能です。
ここで$(4)$式の$M_{l}$は$l$層におけるノード間のMessage Passingの関数、$(5)$式の$U_{l}$は$l$層におけるノード内のUpdateの関数を表します。$M_{l}$、$U_{l}$をシンプルな表記で表す場合は下記のように表すことができます。
$$
\large
\begin{align}
m_{v}^{l+1} &= \sum_{w \in N(v)} c(e_{vw}) h_{w}^{l} \quad (6) \\
h_{v}^{l+1} &= \mathrm{sigmoid}((h_{v}^{l}+m_{v}^{l+1}) W_{v}^{l}) \quad (7) \\
W_{v}^{l} & \in \mathbb{R}^{d \times d}
\end{align}
$$
$(6)$式の$N(v)$はノード$v$に隣接するノードの集合、$c(e_{vw})$はエッジ$e_{vw}$の重みを計算する関数を表します。$d \times d$行列の$W_{v}^{l}$はニューラルネットワークの学習パラメータに対応します。
また、$(7)$式はMLP(Multi Layer Perceptron)の式に対応することも合わせて抑えておくと良いです。$L$層のグラフニューラルネットワークでは$(6), (7)$式のような処理を$L$回繰り返し、次項で確認するようなグラフニューラルネットワークのタスクを解くにあたって活用されます。
グラフニューラルネットワークのタスク設定
グラフニューラルネットワークを用いて解くタスクは主に「①ノード分類」と「②グラフ分類」の$2$つを抑えておくと良いです。「A Comprehensive Survey on Graph Neural Networks」の図がわかりやすいので簡単に確認します。
・ノード分類(Node Classification)
・グラフ分類(Graph Classification)
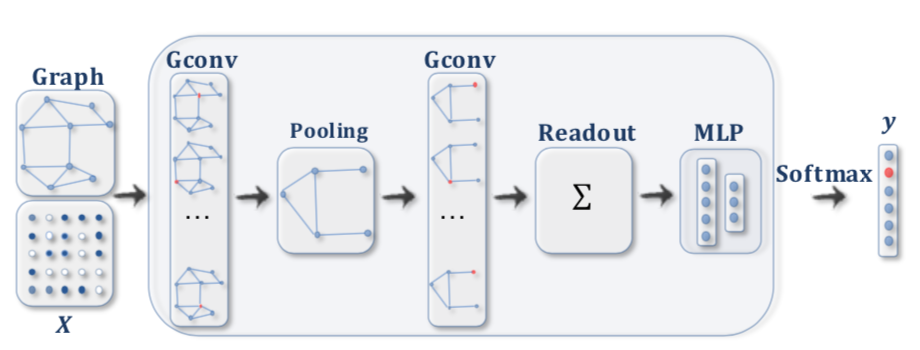
直感的にはたとえば「水泳教室に通う」際に、「生徒」を「ノード」、「スクールへの所属」を「エッジ」で表す場合、個々の生徒の上達を判定することを「ノード分類」、スクール全体の上達を判定することを「グラフ分類」と対応させて理解すると良いと思います。
また、「グラフ分類」を行うことができる場合、「スクール全体の上達」のようなグラフ全体の何らかの特徴量が抽出されたと解釈することもできます。グラフニューラルネットワークの一例であるTransformerではこのように抽出が行われた特徴量を活用して、様々なタスクを解くことが可能になります。
参考
・MPNN論文
・A Comprehensive Survey on Graph Neural Networks
・グラフ理論と機械学習(運営者作成)

[…] […]
[…] グラフニューラルネットワーク(GNN; Graph Neural Network)入門 […]
[…] グラフニューラルネットワーク(GNN; Graph Neural Network)入門 […]