ResNet(Deep Residual Network)の構成の詳細とベンチマークまとめ

ResNetはCNNに基づくDeepLearningにResidual Blockを導入することで層の深いCNNの学習を可能にしたアーキテクチャです。当記事では現在画像認識タスクなどでデフォルトに用いられることが多いResNetの構成の詳細とベンチマークについて取りまとめを行いました。
当記事の作成にあたっては、ResNet論文や「深層学習第$2$版」の第$5$章「畳み込みニューラルネットワーク」の内容などを参考にしました。

・用語/公式解説
https://www.hello-statisticians.com/explain-terms

深層学習　改訂第２版 (機械学習プロフェッショナルシリーズ)

岡谷貴之

2,310円(05/09 19:41時点)

発売日: 2022/01/19

Amazon

Contents

1 前提の確認
- 1.1 畳み込み演算の概要
- 1.2 畳み込み演算の数式
2 Resの構成とパフォーマンス

前提の確認

畳み込み演算の概要

畳み込み演算の数式

フィルタサイズ$W_{f} \times H_{f}$を用いた畳み込みによって出力の$(i,j)$成分$u_{ij}$が計算されるとき、入力に対応する$x$とフィルタに対応する$h$を元に$u_{ij}$は下記のように計算されます。
$$
\large
\begin{align}
u_{ij} = \sum_{p=0}^{W_f-1} \sum_{q=0}^{H_f-1} x_{i+p,j+q} h_{pq}
\end{align}
$$

上記は入力のチャネルとフィルタの枚数が$1$の場合の畳み込みに対応しますが、入力のチャネル数が$C$、フィルタの枚数$C_{out}$枚のとき畳み込みによって出力の$u_{ijk}$成分は下記のように計算されます。
$$
\large
\begin{align}
u_{ijk} = \sum_{c=1}^{C} \sum_{p=0}^{W_f-1} \sum_{q=0}^{H_f-1} x_{i+p,j+q,c} h_{pqck} + b_{k}
\end{align}
$$

上記の$c$は入力のチャネルのインデックス、$k$はフィルタのインデックスにそれぞれ対応します。フィルタのインデックスと出力のチャネルのインデックスが一致することも合わせて確認しておくと良いです。

Resの構成とパフォーマンス

Residual Block

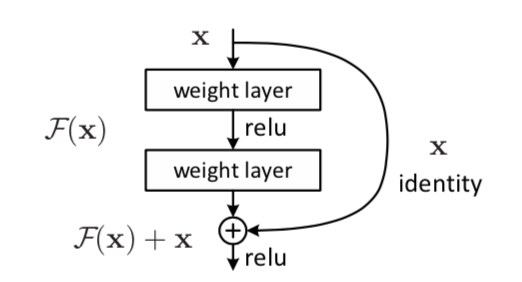
ResNetでは上図のResidual Blockが導入されたことが特徴的です。入力$\mathbf{x}$に対応するパラメータ処理を$\mathcal{F}$と表す場合、AlexNetやVGGNetのようなResNet以前のDeepLearningでは出力を$\mathcal{F}(\mathbf{x})$で計算するのに対し、ResNetでは下記のように計算を行います。
$$
\large
\begin{align}
\mathcal{F}(\mathbf{x}) + \mathbf{x}
\end{align}
$$

このような計算を行うことにより、層の深いDeepLearningにおける勾配消失(vanishing gradients)/勾配爆発(exploding gradients)問題を緩和することが可能になります。たとえば中間層における入力を$\mathbf{h}_{l}$、出力を$\mathbf{h}_{l+1}$とおくとき、Residual Blockの式に基づいて$\mathbf{h}_{l+1} = \mathcal{F}(\mathbf{h}_{l}) + \mathbf{h}_{l}$のように処理が表されます。

このとき、誤差逆伝播の式における$\displaystyle \frac{\partial \mathbf{h}_{l+1}}{\partial \mathbf{h}_{l}}$は下記のように得られます。
$$
\large
\begin{align}
\frac{\partial \mathbf{h}_{l+1}}{\partial \mathbf{h}_{l}} = \frac{\partial \mathcal{F}(\mathbf{h}_{l})}{\partial \mathbf{h}_{l}} + \mathbf{1} \quad (1)
\end{align}
$$

一方でResidual Blockを用いないオーソドックスなDeepLearningにおける$\displaystyle \frac{\partial \mathbf{h}_{l+1}}{\partial \mathbf{h}_{l}}$は下記のように計算されます。
$$
\large
\begin{align}
\frac{\partial \mathbf{h}_{l+1}}{\partial \mathbf{h}_{l}} = \frac{\partial \mathcal{F}(\mathbf{h}_{l})}{\partial \mathbf{h}_{l}} \quad (2)
\end{align}
$$

$(2)$式ではある層のパラメータが全て$0$に近くなった場合、$\displaystyle \frac{\partial \mathbf{h}_{l+1}}{\partial \mathbf{h}_{l}} \simeq 0$となり、誤差逆伝播における以降の勾配が全て零ベクトル/零行列となります。

ある層のパラメータが全て$0$に近くなる場合も$(1)$式が用いられていればそれまでの勾配が等倍されるので勾配が保存されます。

VGG-19とResNetの対応

ResNetの構造は下図のようなVGG-$19$との対応を元に理解すると良いです。

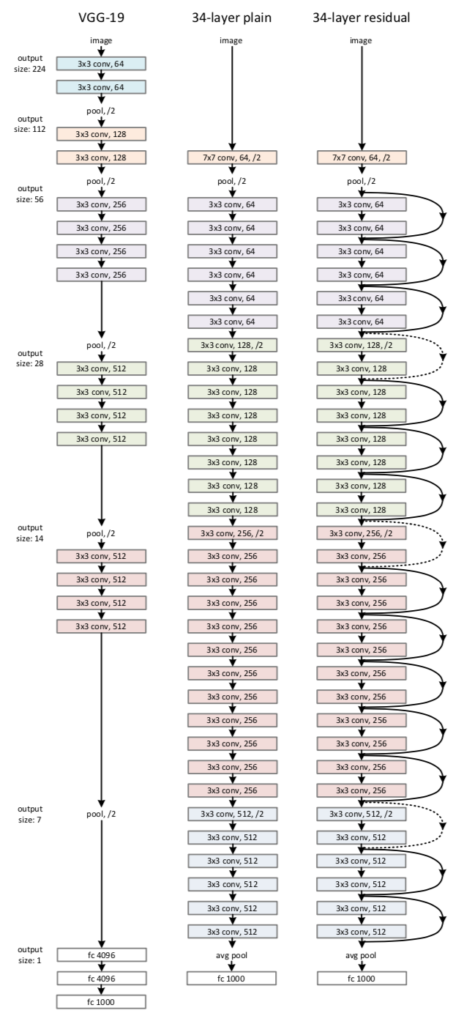
プーリングとダウンサンプリング

前項「VGG-$19$とResNetの対応」の図でVGG-$19$とResNetの対応の確認を行いましたが、一番左のVGG-$19$ではプーリングを行なっているのに対し、真ん中と右側ではプーリングではなくストライドを$2$にすることでダウンサンプリングを行なっていることに注意が必要です。

入門書などのCNNの解説では「畳み込み」と「プーリング」がセットで解説されることが多い一方で、ストライドが$2$以上の畳み込みの二つの処理が代用されることが多くなっているようです¹。

bottleneck構造とResNetの層の数

オーソドックスなResNetでは$3 \times 3$の畳み込みが$2$回繰り返されるところを、$1 \times 1$、$3 \times 3$、$1 \times 1$の$3$回に置き換えた構造をbottleneck構造といいます。bottleneck構造は下図のように表されます。

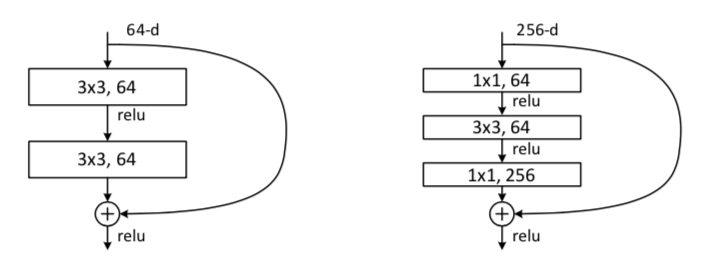
上記のbottleneck構造を元に、ResNetの構成は下記のようなパターンを持ちます。

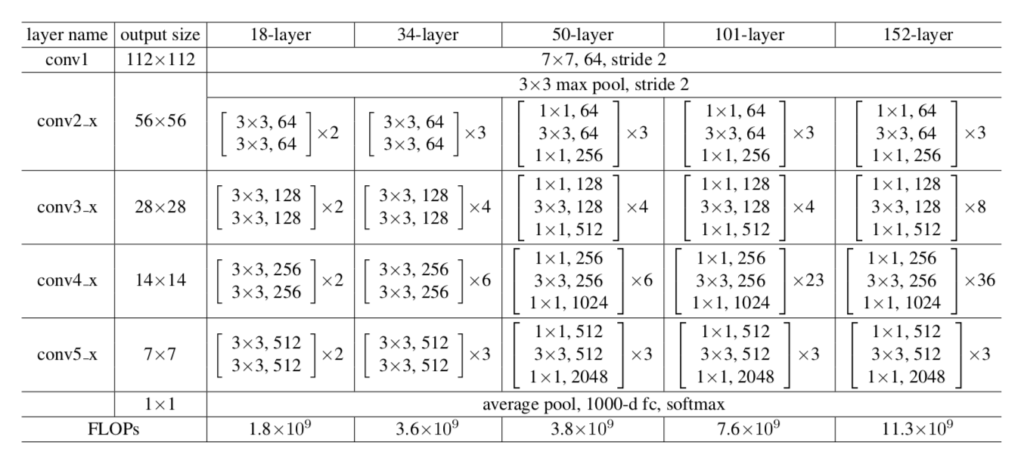
ResNetのパフォーマンス

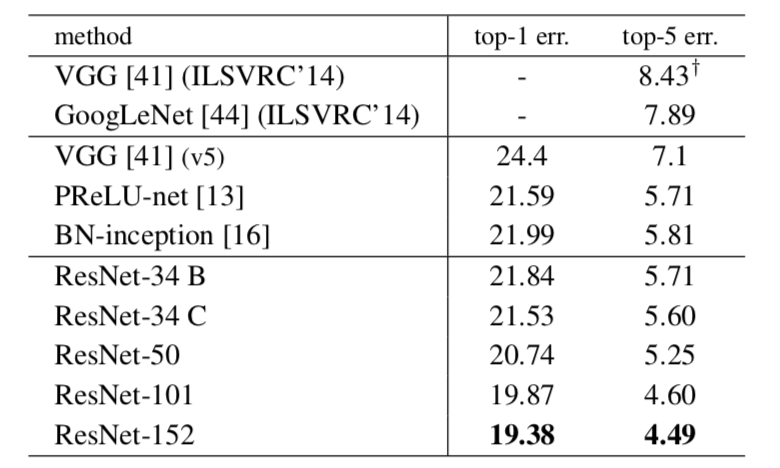
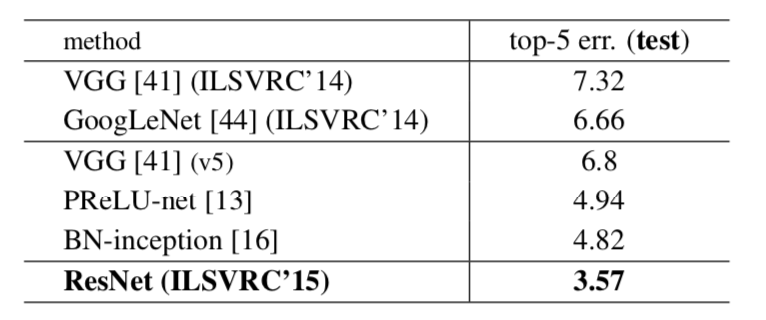
参考

・ResNet論文
 ・VGGNet論文