畳み込み演算を用いて画像のセグメンテーションや生成を行う際に何らかの計算に基づいてアップサンプリング(upsampling)処理が行われます。当記事ではアップサンプリングの際に用いられるdeconvolutionを畳み込み演算を用いて表す一連の流れについて取りまとめを行いました。
当記事の作成にあたっては、「Is the deconvolution layer the same as a convolutional layer?」や「深層学習 第$2$版」の$5.9$節「アップサンプリングと畳み込み」の内容などを参考にしました。
・用語/公式解説
https://www.hello-statisticians.com/explain-terms
転置畳み込み
1Dの畳み込み
ストライド$2$の$1$次元畳み込みの計算は下図のように表すことができる。
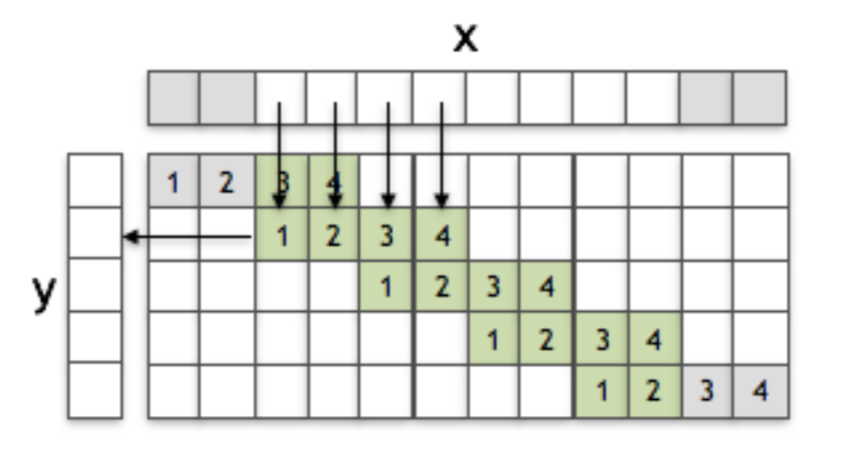
上図からサイズ$8$の$\mathbf{x}$にストライド$2$の畳み込みを行うことでサイズ$5$の$\mathbf{y}$が出力されたと読み取れる。$\mathbf{x}$のグレー部分はパディングを表す。
転置畳み込み
前項の「$1D$の畳み込み」における畳み込みの入力と出力を入れ替えると下図のような計算が得られる。
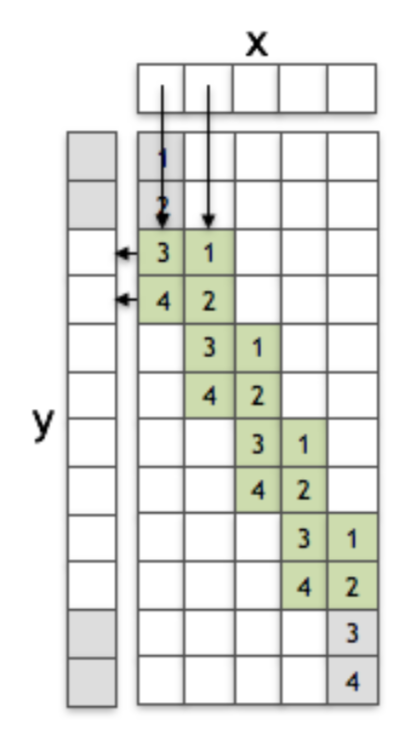
このような処理を転置畳み込み(transposed convolution)という。転置畳み込みは「逆関数」と同様なイメージで解釈すると良い。上図では$\mathbf{x}$のサイズが$5$、$\mathbf{y}$のサイズが$8$であり、「$1D$の畳み込み」の図と逆になったことも合わせて抑えておくと良い。
畳み込みを用いたアップサンプリング
サブピクセル畳み込み
前節の「転置畳み込み」の処理に対し、下図のようにサブピクセル(sub-pixel)を導入することができる。
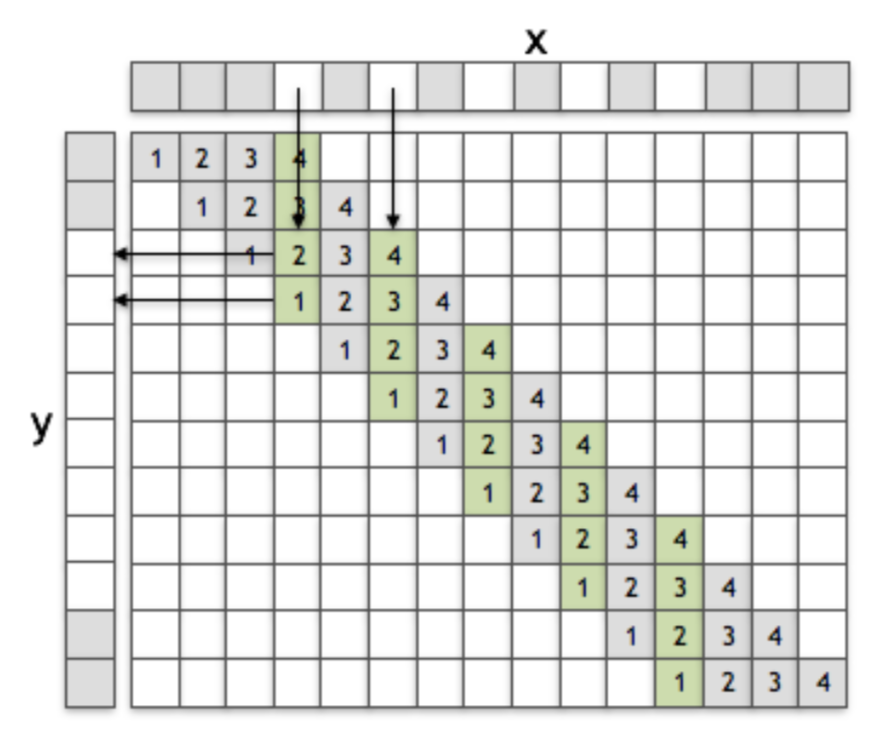
このような処理をサブピクセル畳み込み(sub-pixel convolution)という。$\mathbf{x}$の白のピクセルの間のグレーのピクセルがサブピクセル畳み込みで追加される「サブピクセル」を表す。
サブピクセル畳み込みはアップサンプリング(upsampling)を畳み込み演算によって表した演算であると解釈することもできる。以下、「$2$Dのサブピクセル畳み込み」が「畳み込み演算で表したアップサンプリング処理」と解釈できることについて確認を行う。
2Dのサブピクセル畳み込み
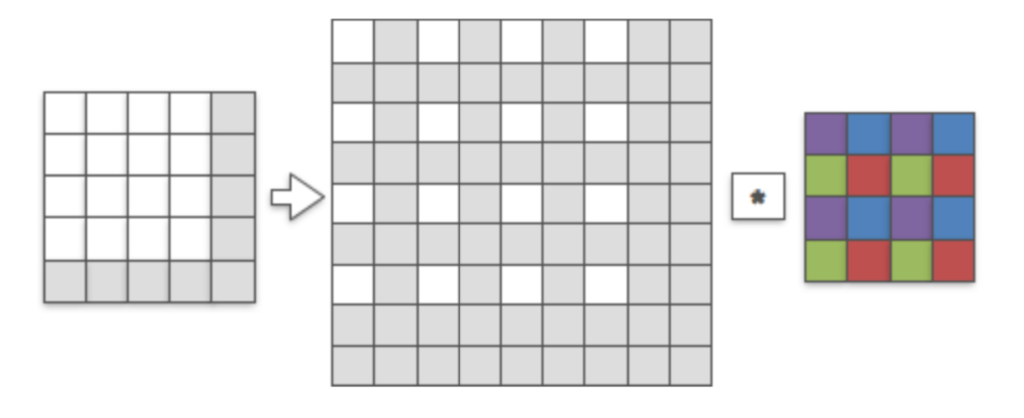
上図のように$2D$の入力に対し、サブピクセル畳み込み(sub-pixel convolution)を行う場合を仮定する。図の$*$は畳み込み演算を表す演算子であり、$*$の「左が入力」、「右が畳み込みに用いるフィルタ」にそれぞれ対応する。グレーで表されたサブピクセルには$0$が入ると仮定する。
一般的な畳み込み演算の原理に基づいてこのサブピクセル畳み込み(sub-pixel convolution)を行うことで下図のような結果が得られる。
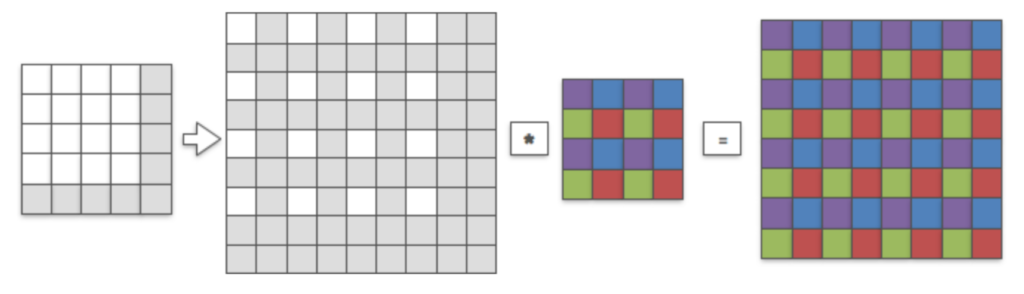
紫の出力が得られるフィルタの位置からフィルタを$1$つ右にずらすと青、$1$つ下にずらすと緑、$1$つ右+$1$つ下にずらすと赤が白のピクセル位置に重なることが確認できるので、出力はこの対応に基づいて理解すると良い。サブピクセル畳み込みを用いたこの演算は下図の演算の結果と対応する。
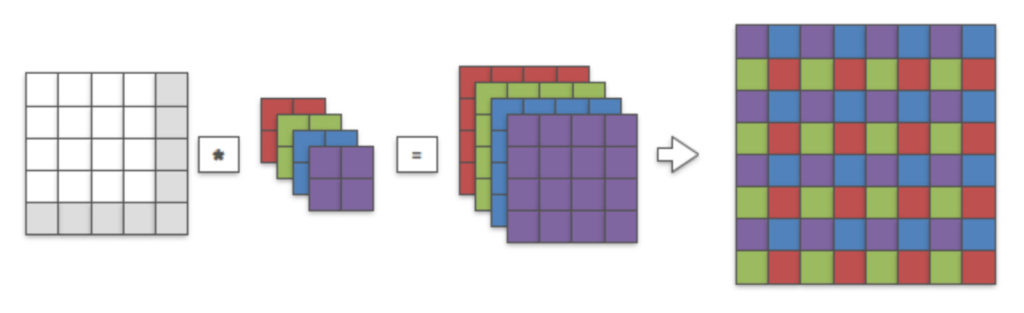
Figure$\, 7$のような処理を用いることでアップサンプリングを行うことができる一方で、Figure$\, 6$を用いれば同様の演算を畳み込みを用いて実現することができる。
このようにアップサンプリングも畳み込み演算で表せることは抑えておくと良い。
