活性化関数(activation function)のグラフの図示

DeepLearningの順伝播の計算では隠れ層におけるそれぞれのニューロンでなんらかの判断が行われるように非線形関数である活性化関数(activation function)を用います。当記事では活性化関数のいくつかの例の数式の確認とグラフの図示を行いました。

・用語/公式解説
https://www.hello-statisticians.com/explain-terms

活性化関数

活性化関数の概要

活性化関数の数式

・シグモイド関数
$$
\large
\begin{align}
y = \frac{1}{1+e^{-x}} = \frac{e^{x}}{e^{x}+1}
\end{align}
$$

・ソフトサイン関数
$$
\large
\begin{align}
y = \frac{1}{1+e^{-x}} = \frac{x}{1+|x|}
\end{align}
$$

・ソフトプラス関数
$$
\large
\begin{align}
y = \log{(1+e^{x})}
\end{align}
$$

・ReLU(ランプ関数)
$$
\large
\begin{align}
y = \max{(0,x)}
\end{align}
$$

・双曲線正接関数
$$
\large
\begin{align}
y = \tanh{x} = \frac{e^{x}-e^{-x}}{e^{x}+e^{-x}}
\end{align}
$$

活性化関数のグラフ

シグモイド関数

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns

sns.set_theme()

x = np.arange(-5., 5.01, 0.01)
y_1 = 1./(1.+np.e**(-x))

plt.plot(x, y_1)
plt.show()

・実行結果

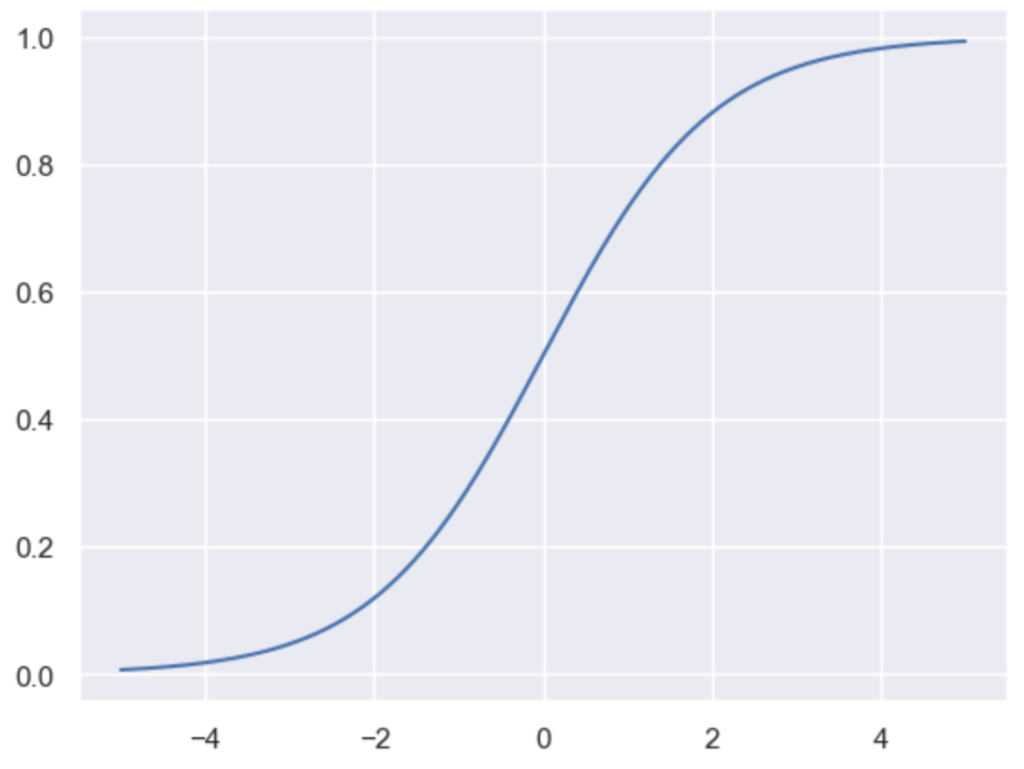
ソフトサイン関数

y_2 = x/(1+np.abs(x))

plt.plot(x, y_2)
plt.show()

・実行結果

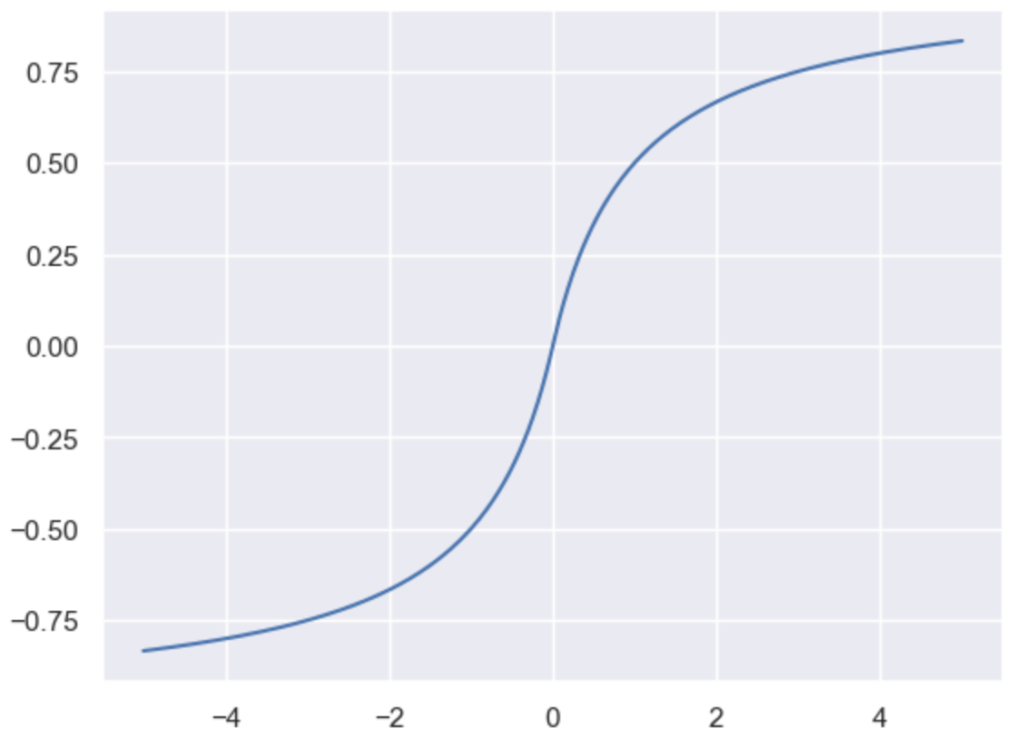
ソフトプラス関数

y_3 = np.log(1+np.e**x)

plt.plot(x, y_3)
plt.show()

・実行結果

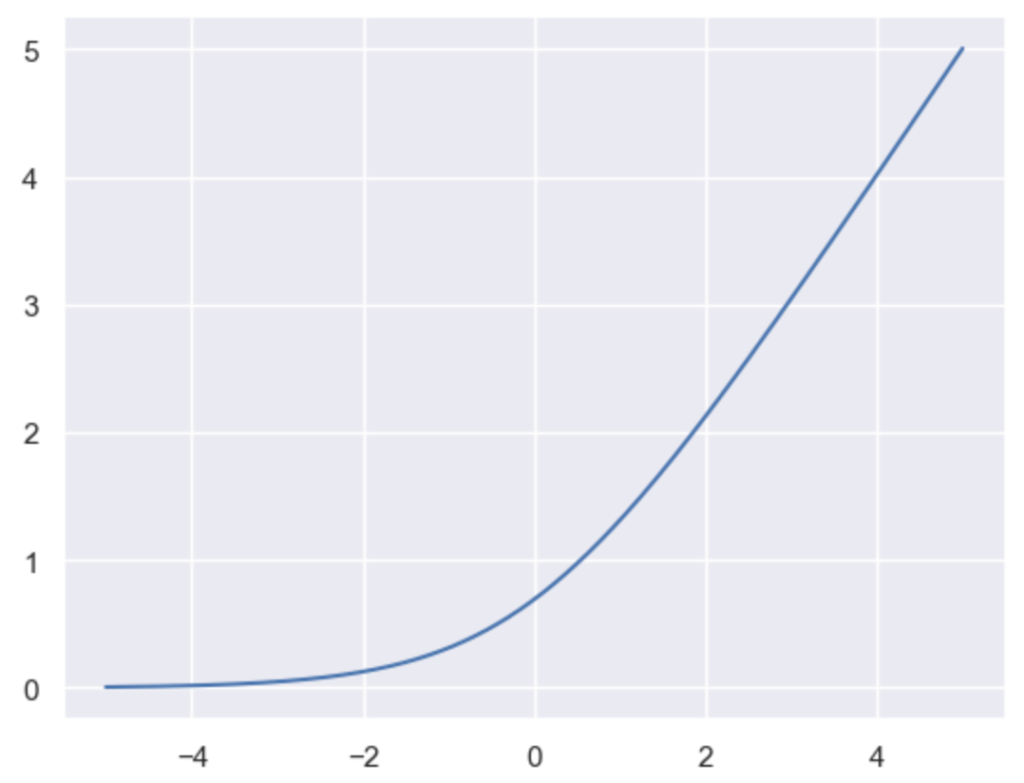
ReLU(ランプ関数)

x_ = np.zeros([x.shape[0],2])
x_[:,1] = x
y_4 = np.max(x_, axis=1)

plt.plot(x, y_4)
plt.show()

・実行結果

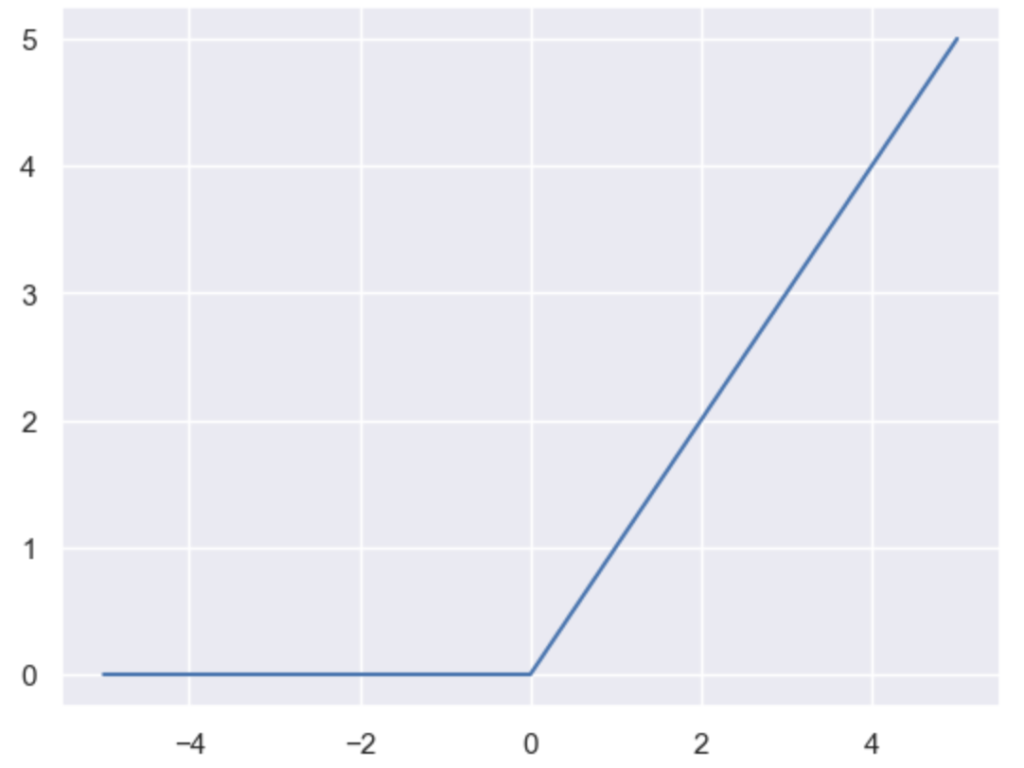
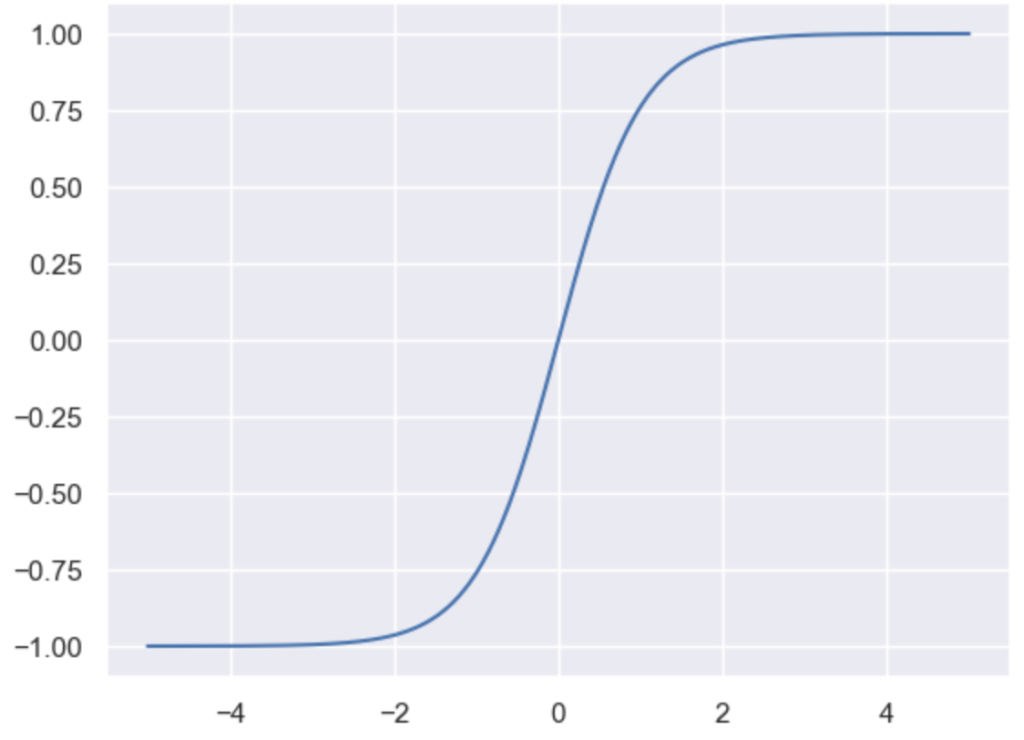
双曲線正接関数(hyperbolic tangent function)

y_5 = (np.e**x - np.e**(-x)) / (np.e**x + np.e**(-x))

plt.plot(x, y_5)
plt.show()

・実行結果

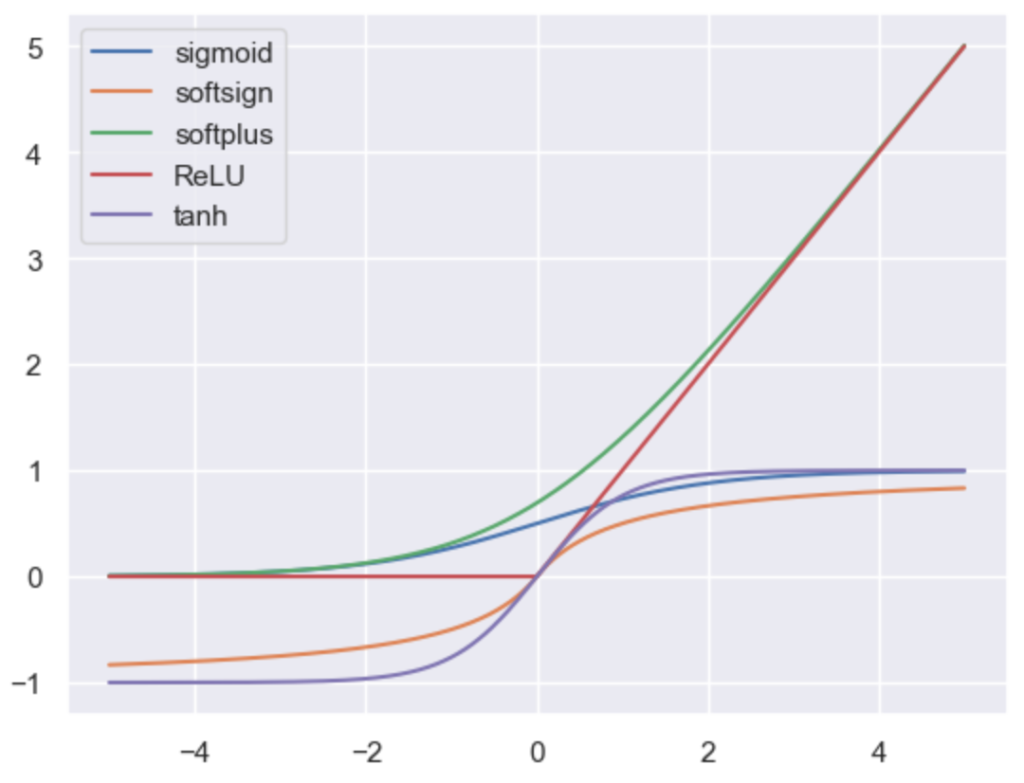
グラフまとめ

plt.plot(x, y_1, label="sigmoid")
plt.plot(x, y_2, label="softsign")
plt.plot(x, y_3, label="softplus")
plt.plot(x, y_4, label="ReLU")
plt.plot(x, y_5, label="tanh")

plt.legend()
plt.show()

・実行結果