TransformerにおけるSoftmax関数の計算量とLinear Transformer

Transformerは汎用的に用いることのできる強力なDeepLearningである一方、入力系列のトークンが多くなると計算量も増大します。当記事ではTransformerの各Attention処理でのSoftmax計算の軽減にあたっての研究である、Linear Transformer論文について取りまとめました。
作成にあたってはLinear Transformer論文や、「A Survey of Transformers」の内容を参考にしました。

・用語/公式解説
https://www.hello-statisticians.com/explain-terms

前提の確認

Transformerの仕組みの概要

Dot Product Attentionに主に基づくTransformerの仕組みについては既知である前提で当記事はまとめました。下記などに解説コンテンツを作成しましたので、合わせて参照ください。

・直感的に理解するTransformer(統計の森作成)

Transformerの式表現

TransformerのDot Product Attentionは下記のような式で定義されます¹。
$$
\large
\begin{align}
\mathrm{Attention}(Q, K, V) &= \mathrm{Softmax} \left( \frac{Q K^{\mathrm{T}}}{\sqrt{d}} \right) V \quad (1) \\
Q, K, V & \in \mathbb{R}^{n \times d}
\end{align}
$$

Linear Transformer

Linear Transformerの概要

Linear Transformerの概要は下図を確認すると理解しやすいです。

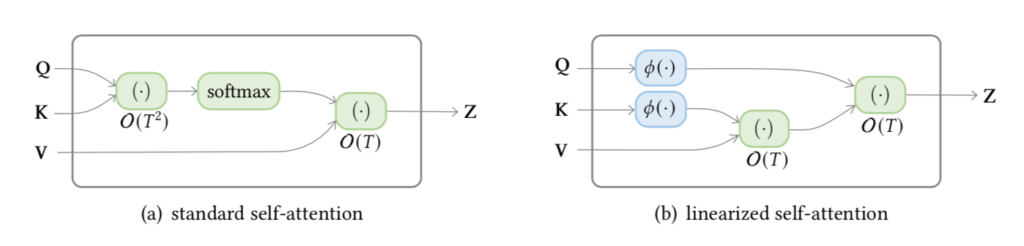
上図の左側が一般的なTransformerの計算フロー、右側がLinear Transformerにおける計算フローに対応します。左側のTransformerでは$Q, K \in \mathbb{R}^{n \times d}$について$Q K^{\mathrm{T}} \in \mathbb{R}^{n \times n}$の行毎(row-wise)にソフトマックス関数を適用する際に、計算量が入力するトークン数$n$の二乗になります。図では$T=n$であり、計算量が$\mathcal{O}(T^{2})$で表現されています。オリジナルのTransformerでは$n \simeq d$を前提としている一方で、Linear TransformerではReformerなどと同様に$n >> d$の場合を仮定することに注意しておくと良いです。

Linear Transformerの論文ではこのようなソフトマックス関数の計算時の計算量を軽減するにあたって、ソフトマックス関数の$\exp$の代わりにfeature mapの$\phi$が導入されます。$\exp$を用いないことで行列の積の順序を変えることが可能になることに注意しておくと良いです。

Transformerの式の改変

$(1)$式の出力の$i$行目を縦ベクトルの$z_{i}$とおくと、$Q \in \mathbb{R}^{n \times d}$の$i$行目の$q_{i}$に対応する$z_{i}$は下記のように表すことが可能です。
$$
\large
\begin{align}
z_{i}^{\mathrm{T}} = \mathrm{Attention}(q_{i}^{\mathrm{T}}, K, V) = \mathrm{Softmax} \left( \frac{q_{i}^{\mathrm{T}} K^{\mathrm{T}}}{\sqrt{d}} \right) V \quad (2)
\end{align}
$$

ここで$K, V \in \mathbb{R}^{n \times d}$の$j$行目を$k_{j}, v_{j} \in \mathbb{R}^{d}$のように表すとき、$(2)$式は下記のように表すこともできます。
$$
\large
\begin{align}
z_{i} &= \left[ \mathrm{softmax}{\left( q_{i}^{\mathrm{T}} K^{\mathrm{T}} \right)} V \right]^{\mathrm{T}} \\
&= \sum_{k=1}^{n} \left[ \frac{\mathrm{sim}(q_{i}, k_{k})}{\sum_{j=1}^{n} \mathrm{sim}(q_{i}, k_{j})} v_{j} \right] \quad (3) \\
\mathrm{sim}(q, k) &= \exp{ \left( \frac{q^{\mathrm{T}} k}{\sqrt{d}} \right) }
\end{align}
$$

上記の$q_{i}, k_{j}, v_{j}$は$Q, K, V$の$i$行目や$j$行目を抜き出して縦ベクトルで表されたものに対応します²。出力の$z_{i}$も同様に縦ベクトルであることにご注意ください。よって、たとえば$q_{i}, k_{j}$の内積は$q_{i}^{\mathrm{T}} k_{j}$のように表されます。

Linear Transformerの数式

$(3)$式の$\mathrm{sim}(q_{i}, k_{k})$を下記のように$\phi(x)$を用いて表す場合を仮定します。
$$
\large
\begin{align}
\mathrm{sim}(q_{i}, k_{k}) = \phi(q_{i})^{\mathrm{T}} \phi(k_{k}) \quad (4)
\end{align}
$$

$(4)$式に基づいて$(3)$式は下記のように改変することができます。
$$
\large
\begin{align}
z_{i} &= \sum_{k=1}^{n} \left[ \frac{\mathrm{sim}(q_{i}, k_{k})}{\sum_{j=1}^{n} \mathrm{sim}(q_{i}, k_{j})} v_{k} \right] \quad (3) \\
&= \sum_{k=1}^{n} \left[ \frac{\phi(q_{i})^{\mathrm{T}} \phi(k_{k})}{\sum_{j=1}^{n} \phi(q_{i})^{\mathrm{T}} \phi(k_{j})} v_{k} \right] \\
&= \left[ \frac{\phi(q_{i})^{\mathrm{T}} \sum_{k=1}^{n} \phi(k_{k}) v_{k}^{\mathrm{T}}}{\phi(q_{i})^{\mathrm{T}} \sum_{j=1}^{n} \phi(k_{j})} \right]^{\mathrm{T}} \quad (5)
\end{align}
$$

$(5)$式は下記のような行列の積の形式で表すこともできます。
$$
\large
\begin{align}
\left( \phi(Q) \phi(K)^{\mathrm{T}} \right) V = \phi(Q) \left( \phi(K)^{\mathrm{T}} V \right) \quad (6)
\end{align}
$$

$(5)$式や$(6)$式の右辺の計算の計算量は$\mathcal{O}(N)$であり、「Linear Transformerの概要」の図に対応します。

また、Linear Transformerでは$\phi(x)$を下記のように定義します。
$$
\large
\begin{align}
\phi(x) = \mathrm{elu}(x) + 1
\end{align}
$$

上記の$\mathrm{elu}$関数については次項の「exponential linear unit」で詳しく確認を行います。

exponential linear unit

exponential linear unitの略であるelu関数$\mathrm{elu}(x)$は下記のような式で定義されます。
$$
\large
\mathrm{elu}(x) =
\begin{cases}
x & \mathrm{if} \, x > 0 \\
\alpha(\exp{(x)}-1) & \mathrm{if} \, x \leq 0
\end{cases}
$$

また、$\mathrm{elu}(x)$関数の$x$についての微分は下記のように表されます。
$$
\large
\frac{d}{dx} \mathrm{elu}(x) =
\begin{cases}
1 & \mathrm{if} \, x > 0 \\
\alpha \exp{(x)} = \mathrm{elu}(x) + \alpha & \mathrm{if} \, x \leq 0
\end{cases}
$$

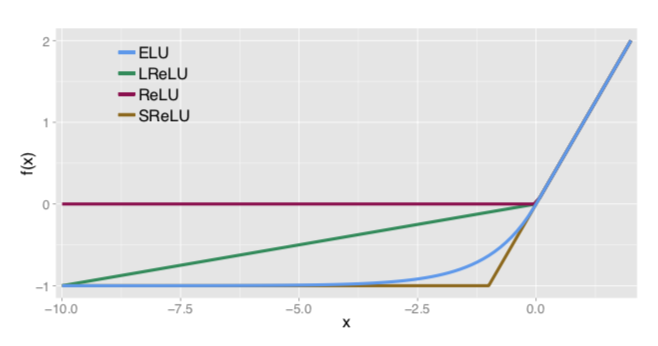
ELUはReLUのような活性化関数に用いるにあたって考案されており、下記のようなグラフでも表すことができます。

NumPyを用いた計算による実験

以下$(6)$式に基づいて、$Q, K, V \in \mathbb{R}^{N \times D}$の場合のDot Product Attentionの計算時間を$N$の値を変えて計測を行います。

$N=10{,}000, D=500$

$N=10{,}000, D=500$のとき、$Q(K^{\mathrm{T}}V)$の計算時間は下記のようになります。

import numpy as np
import time

import numpy as np
import time

N = 10000
D = 500

Q = np.ones([N, D])
K = np.ones([N, D])
V = np.ones([N, D])

start = time.time()
V_1 = np.dot(Q, np.dot(K.T, V))
end = time.time()

time_diff = end - start
print("{:.3f}".format(time_diff))

・実行結果

0.209

同様に$(QK^{\mathrm{T}})V$の計算時間は下記のようになります。

start = time.time()
V_1 = np.dot(Q, np.dot(K.T, V))
end = time.time()

time_diff = end - start
print("{:.3f}".format(time_diff))

・実行結果

3.270

$N=20{,}000, D=500$

$N=20{,}000, D=500$のとき、$Q(K^{\mathrm{T}}V)$の計算時間は下記のようになります。

N = 20000
D = 500

Q = np.ones([N, D])
K = np.ones([N, D])
V = np.ones([N, D])

start = time.time()
V_1 = np.dot(Q, np.dot(K.T, V))
end = time.time()

time_diff = end - start
print("{:.3f}".format(time_diff))

・実行結果

0.389

同様に$(QK^{\mathrm{T}})V$の計算時間は下記のようになります。

start = time.time()
V_1 = np.dot(Q, np.dot(K.T, V))
end = time.time()

time_diff = end - start
print("{:.3f}".format(time_diff))

・実行結果

12.354

$N=10{,}000$、$N=20{,}000$の結果より、$N$が大きくなるにつれて$Q(K^{\mathrm{T}}V)$の計算量が$\mathcal{O}(N)$、$(QK^{\mathrm{T}})V$の計算量が$\mathcal{O}(N^2)$であることが概ね確認できます³。

参考

・Linear Transformer論文
・A Survey of Transformers
・ELU(Exponential Linear Unit)論文

1. ここではTransformerに入力するトークン数を$n$、トークンの特徴量ベクトルの次元を$d$で表しました。「Linear Transformerの概要」で用いた図の$T$は$n$と一致することにご注意ください。 ↩︎
2. 行列の$i$行目や$j$行目を縦ベクトルで表すというのはミスリードになりやすいかもしれませんが、Linear Transformerの論文の表記に合わせました。 ↩︎
3. 計測自体はかなり雑なので、値はそれほど参考にしないようにご注意ください。ここでは$Q(K^{\mathrm{T}}V)$の順に計算すると速いことの確認を主な目的に計測を行いました。 ↩︎