【ViT論文まとめ】Computer Vision分野へのTransformerの応用

Transformerは元々機械翻訳タスクに対して考案された一方で、大域的な特徴量を取り扱うことのできる強力なモジュールであることから様々なタスクに応用されます。当記事ではTransformerを画像処理に応用した初期の研究であるViT(Vision Transformer)について取りまとめました。
ViTの論文である「An image is worth 16×16 words: Transformers for image recognition at scale.」の内容を参考に作成を行いました。

・用語/公式解説
https://www.hello-statisticians.com/explain-terms

前提の確認

Transformerの概要

Dot Product Attentionに主に基づくTransformerの仕組みについては既知である前提で当記事はまとめました。下記などに解説コンテンツを作成しましたので、合わせて参照ください。

・直感的に理解するTransformerの仕組み(統計の森作成)

ネットワーク分析から直感的に理解するTransformerの仕組みと処理の流れ

ViT

処理の概要

Vision Transformer(ViT)の処理の全体像は下図を元に掴むと良いです。

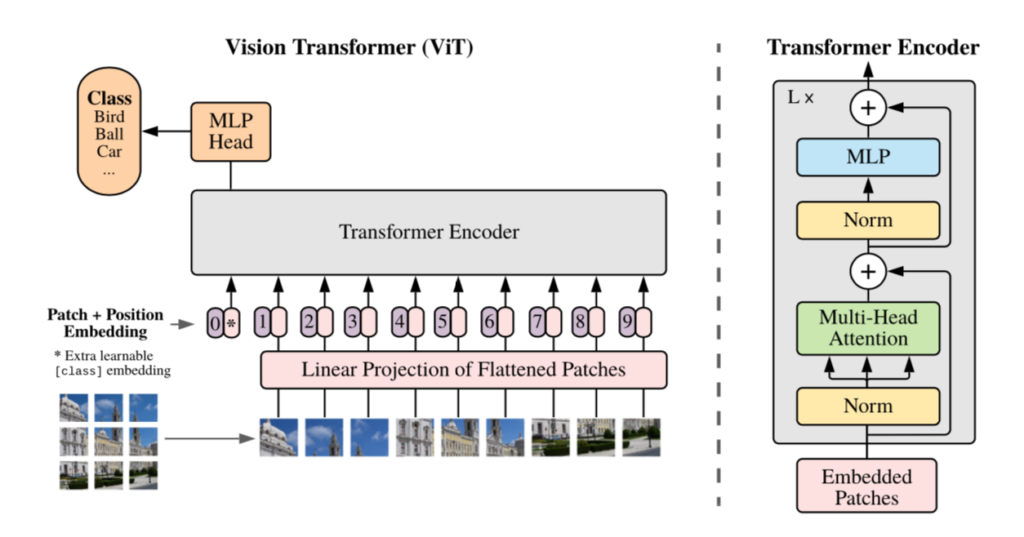
Vision Transformerでは入力画像を$16 \times 16$ピクセルのように一定サイズで区切りパッチ(patch)を作成し、それぞれのパッチをトークンと見なしてTransformerの処理を実行します。上図では左下の入力画像を$9$つに分割し、Transformer Encoderに入力されます。

この処理における「パッチのトークン化」や「パッチへのPositional Embeddingの追加」については次項以降で詳しく確認します。

パッチのトークン化

ViTではまず入力画像を$X \in \mathbb{R}^{H \times W \times C}$をパッチ集合に対応する行列$X_{p} \in \mathbb{R}^{N \times (P^{2} \cdot C)}$へリサイズを行います。ここで$N$は下記のように計算されます。
$$
\large
\begin{align}
H \times W \times C &= N \times (P^{2} \cdot C) \\
N &= \frac{HW \cancel{C}}{P^{2} \cancel{C}} \\
&= \frac{HW}{P^{2}}
\end{align}
$$

上記の$\displaystyle N = \frac{HW}{P^{2}}$は「パッチの数はグレースケールにおける全ピクセル数($HW$)を各パッチのピクセル数$P^{2}$で割った数に一致する」と解釈するとわかりやすいと思います¹。

ここでリサイズによって得た$X_{p}$の$i$行目を$\mathbf{x}_{p}^{i} \in \mathbb{R}^{1 \times (P^{2} C)}$のようにおくと、$i$番目のパッチの$D$次元のEmbeddingは下記のように定義されます。
$$
\large
\begin{align}
\mathbf{x}_{p}^{i} E & \in \mathbb{R}^{1 \times D} \\
\mathbf{x}_{p}^{i} & \in \mathbb{R}^{1 \times (P^{2} C)}, \, E \in \mathbb{R}^{(P^{2} C) \times D}
\end{align}
$$

ここでBERTと同様にTransformer演算から全体の特徴量を抽出する用のパッチ$\mathbf{x}_{cls} \in \mathbb{R}^{1 \times D}$とPositional Encodeingの$E_{pos} \in \mathbb{R}^{(N+1) \times D}$を元に下記のように$\mathbf{z}_{0}$を定義します。
$$
\large
\begin{align}
\mathbf{z}_{0} = \left( \begin{array}{c} \mathbf{x}_{cls} \\ \mathbf{x}_{p}^{1} E \\ \mathbf{x}_{p}^{2} E \\ \vdots \\ \mathbf{x}_{p}^{N-1} E \\ \mathbf{x}_{p}^{N} E \end{array} \right) + E_{pos} \quad (1)
\end{align}
$$

上記はViT論文の$(1)$式に対応します。また、$\mathbf{x}_{cls}, \, E, \, E_{pos}$はどれも学習時に同時に学習されるパラメータです。ViTでは$(1)$式で定義される$\mathbf{z}_{0} \in \mathbb{R}^{(N+1) \times D}$に対し、Transformerの処理を適用し、特徴量の抽出を行います。

パッチのPositonal Embedding

前項で取り扱ったようにViTでは学習によってPositonal Embeddingの値を取得します。このようなPositonal Embeddingの取得はBERTやGPTなどでも用いられています。

ViT-Base/ViT-Large/ViT-Huge

ViT論文ではViT-Base/ViT-Large/ViT-Hugeの三つが主に用いられます。それぞれのハイパーパラメータは下記の表より確認できます。

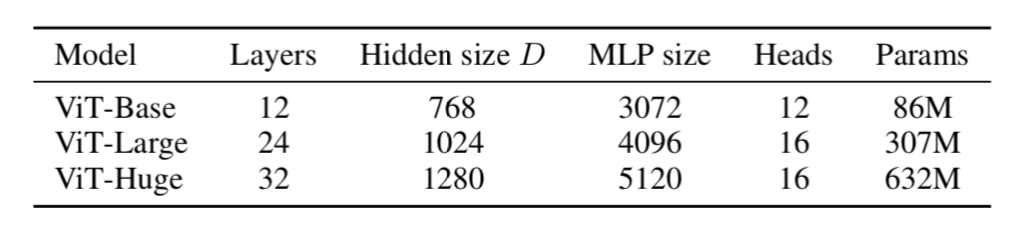
BERTと同様な規模感で把握しておくと良いと思います。パッチサイズは基本的に$P=16$が用いられます。

参考

・Transformer論文：Attention is All you need[$2017$]
・ViT論文

1. RGBであれば$3HW$と$3P^{2}$、チャネル数$C$の場合は$HWC$と$P^{2} C$がそれぞれ対応します。解釈のわかりやすさを優先するにあたって、グレースケールを例に出しました。 ↩︎