ViTなどのComputer Vision分野へのTransformerの導入は強力なアプローチである一方で、Transformerをそのまま用いる場合は局所相関を生かせないなどの課題があります。当記事ではViTに畳み込みを導入した手法であるCvTを題材に畳み込みとMultiHead Attentionの対応について取りまとめました。
CvTの論文である「CvT: Introducing Convolutions to Vision Transformers」の内容を参考に作成を行いました。
・用語/公式解説
https://www.hello-statisticians.com/explain-terms
Contents
前提の確認
Transformerの概要
Dot Product Attentionに主に基づくTransformerの仕組みについては既知である前提で当記事はまとめました。下記などに解説コンテンツを作成しましたので、合わせて参照ください。
・直感的に理解するTransformerの仕組み(統計の森作成)
ViT
Convolutional vision Transformer
処理の概要
Convolutional vision Transformer(CvT)の処理の全体像は下図を元に掴むと良いです。
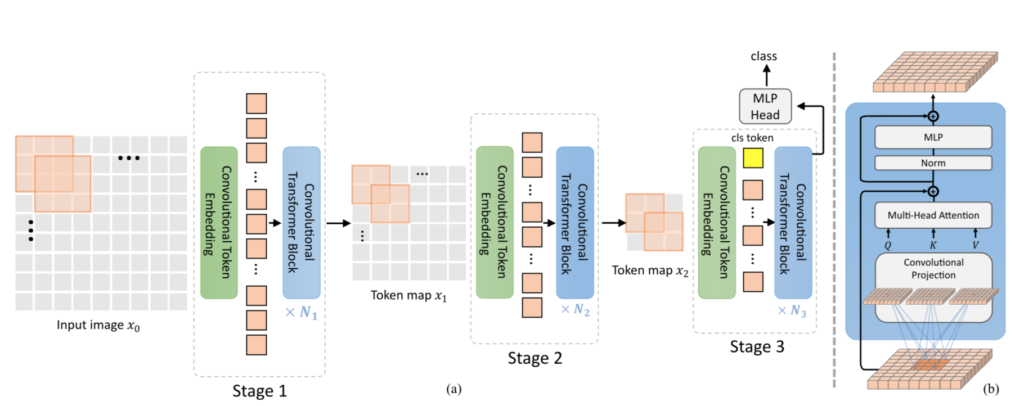
CvTは主に「Convolutional Token Embedding」と「Convolutional Transformer Block」の二つによって構成され、どちらの処理にも畳み込みが用いられます。
「Convolutional Transformer Block」は「Convolutional Projection」という手法を用いてTransformerモジュールの入力であるQuery、Key、Valueの作成を行い、Transformer計算を行います。上図の$(\mathrm{b})$で示されるように、「Convolutional Projection」以外の「Convolutional Transformer Block」の処理はオーソドックスなTransformerであるので、以下では「Convolutional Token Embedding」と「Convolutional Projection」について詳しく取り扱います。
Convolutional Token Embedding
ステージ$i-1$の出力を$X_{i-1} \in \mathbb{R}^{H_{i-1} \times W_{i-1} \times C_{i-1}}$とおき、下記が成立するようにチャネル数$C_i$、フィルタのサイズが$s \times s$の畳み込み演算に対応する関数$f$を定義します。
$$
\large
\begin{align}
f(X_{i-1}) \in \mathbb{R}^{H_{i} \times W_{i} \times C_{i}}
\end{align}
$$
このとき、上記で表される関数の$f$が「Convolutional Token Embedding」に対応します。ステージ毎のフィルタサイズ$s \times s$は下記の表から確認できます。
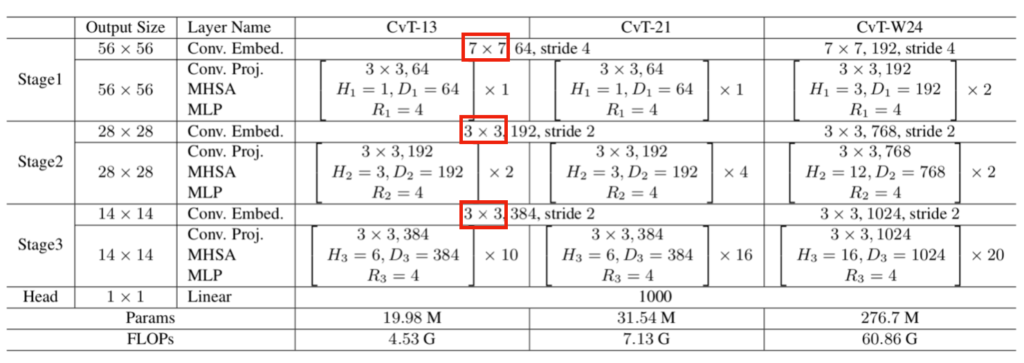
赤枠で囲った部分がフィルタサイズに対応します。また、「Convolutional Token Embedding」がステージ毎に$1$度であるのに対し、「Convolutional Transformer Block」は複数回繰り返される場合があることも合わせて抑えておくと良いです。
Convolutional Projection
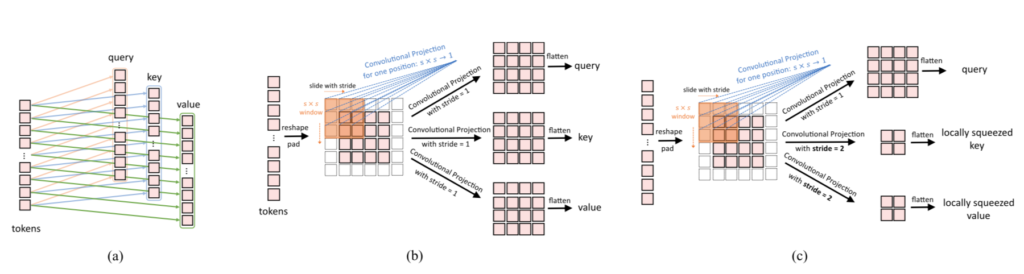
「Convolutional Projection」の処理概要は上図の$(\mathrm{b})$を元に理解すると良いです。パッチを$2D$に並べ、畳み込みを行なうことでQuery、Key、Valueを計算します。ここでの畳み込みではオーソドックスな畳み込みではなくDepth-wise Convolution」と「Point-wise Convolution」を組み合わせた「Depth-wise Separable Convolution」が用いられます。「Depth-wise Separable Convolution」については下記で詳しく取り扱ったので当記事では省略します。
また、処理概要を掴むにあたっては図の$(\mathrm{b})$が適している一方で、実際には$(\mathrm{c})$のSqueezed convolutional projectionが用いられます。Squeezed convolutional projectionはKeyとValueの解像度を低くすることでSpatial Reduction Attention(SRA)と同様に計算の軽量化を行なったと解釈すると良いと思います。Spatial Reduction Attentionについては下記で詳しく取り扱ったので当記事では省略します。
畳み込みとMultiHead Attentionの対応
前項では「Convolutional Transformer Block」におけるTransformerモジュールへの入力となるQuery、Key、Valueの作成を行う「Convolutional Projection」について確認を行いました。当項ではこの「Convolutional Projection」の解釈についてMultiHead Attentionの処理と対応させることで確認を行います。まず、Point-wise Convolutionに一致する$1 \times 1$の畳み込みはMultiHead Attentionにおけるlinear projectionと同じ処理を表すことを抑えておくと良いです。
「Point-wise Convolution」と「MultiHead Attentionにおけるlinear projection」の対応について詳しく確認するにあたって、Feature Mapの$X \in \mathbb{R}^{H \times W \times C_1}$とフィルタの$w_{i} \in \mathbb{R}^{C_1}$を定義します。
このとき、$X$の空間の$2D$を$1D$に直す(Flatten)ことで$X’ \in \mathbb{R}^{HW \times C_1}$を得ることができます。ここで入力のチャネル数の$C_1$に対応する出力のチャネル数を$C_2$とおき、下記のようにフィルタのパラメータを行列$\mathcal{W}$で定義します。
$$
\large
\begin{align}
\mathcal{W} = \left( \begin{array}{ccccc} w_1 & \cdots & w_i & \cdots & w_{C_2} \end{array} \right)
\end{align}
$$
上記を元に$X’ \mathcal{W}$を計算し、$1D$から$2D$に戻す処理はPoint-wise Convolutionの演算に一致します1。
一方、$X’$を$Q, K, V$、$\mathcal{W}$を$W^{Q}, W^{K}, W^{V}$に読み換えた処理はMultiHead Attentionの「linear projection」の定義式そのものであることも同時に確認できます。したがって、「Point-wise Convolution」と「MultiHead Attentionにおけるlinear projection」は基本的に同一な処理であることが確認できます。
この処理の対応から、「Convolutional Projection」は新規の処理というよりはMultiHead Attentionの拡張であると解釈することができます。
参考
・Transformer論文:Attention is All you need[$2017$]
・Convolutional vision Transformer論文
- CNNの実装では畳み込みをそのまま実装するとループ計算が多くなるので、フィルタと行列演算ができるようにここで取り扱ったような空間方向に展開してから元に戻すような実装がよく用いられます。DeepLearningのフレームワークでは
im2colなどの名称でこのような機能が提供されることが多いです。 ↩︎

[…] 【CvT論文まとめ】畳み込みとMultiHead Attentionの対応 【SegFormer】Transformerを用いたシンプルかつ効率的なセグメンテーション […]