Pyramid ViTとSpatial Reduction Attention

Transformerを用いてセグメンテーション(Segmentation)やObject DetectionのようなDense Predictionタスクを学習させるには解像度を高くする必要がある一方で、ViTでは解像度を高くすると計算量の問題が生じます。当記事ではこの解決にあたって考案されたSRA(Spatial Reduction Attention)に基づくPyramid Vision Transformer(PVT)の論文について取りまとめを行いました。PVTの論文である「Pyramid Vision Transformer: A Versatile Backbone for Dense Prediction without Convolutions」の内容を参考に作成を行いました。

・用語/公式解説
https://www.hello-statisticians.com/explain-terms

前提の確認

Transformerの概要

Dot Product Attentionに主に基づくTransformerの仕組みについては既知である前提で当記事はまとめました。下記などに解説コンテンツを作成しましたので、合わせて参照ください。

・直感的に理解するTransformerの仕組み(統計の森作成)

ネットワーク分析から直感的に理解するTransformerの仕組みと処理の流れ

ViT

【ViT論文まとめ】Computer Vision分野へのTransformerの応用

Pyramid Vision Transformer

処理の概要

Pyramid Vision Transformer(PVT)の処理の全体像は下図を元に掴むと良いです。

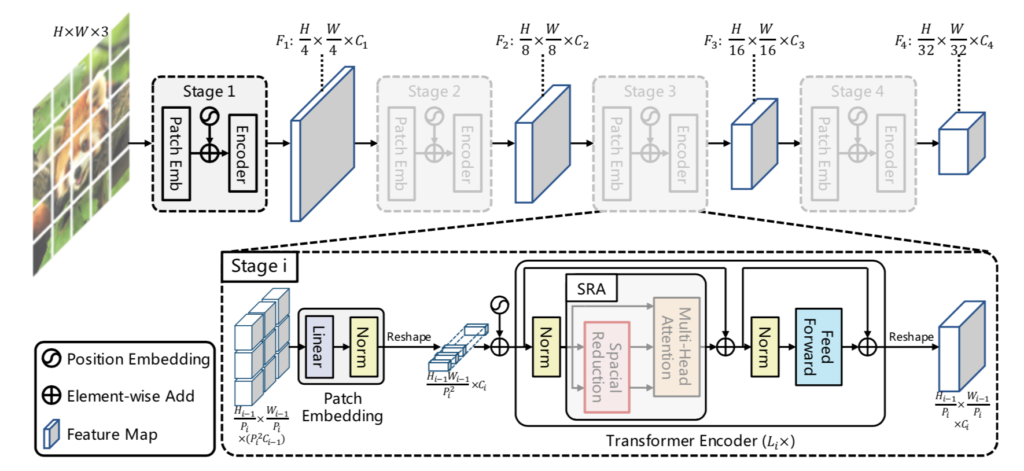
基本的にはViTの処理と同じである一方で、$16 \times 16$のピクセルをパッチと見なすViTに対してPyramid Vision Transformerではまず$4 \times 4$のピクセルをパッチと見なし、ステージ(stage)単位で徐々に解像度を粗くします。

各ステージの処理は「Patch embedding」と「Transformer encoder」に分けられます。大まかには前処理とTransformer処理のように解釈しておくと良いと思います。

ハイパーパラメータの定義と基本的な設定

Pyramid Vision Transformerではステージ単位で処理を行います。ステージ$i$におけるハイパーパラメータはそれぞれ下記のように定義されます。

ハイパーパラメータ	意味
$F_i$	ステージ$i$におけるFeature Mapの縮小率。$F_1=4, F_2=8, F_3=16, F_4=32$である。
$P_i$	ステージ$i$におけるパッチのサイズ。基本的には$P_1=4$、$i \geq 2$では$P_i=2$。ステージ$i-1$の出力をベースにパッチのサイズを定義することに注意。
$C_i$	ステージ$i$の出力のチャネル数。解像度が低くなるにつれて$C_i$は大きくなる。
$L_i$	ステージ$i$におけるTransformer encoderの層の数。特に$i=2, 3$のときにモデルが大きくなるにつれて$L_i$は大きくなる。
$R_i$	ステージ$i$のSpatial Reduction Attentionにおけるreduction ratio。$R_i$が大きくなるにつれてAttentionにおける解像度が粗くなる。
$N_i$	ステージ$i$におけるAttentionのヘッドの数。
$E_i$	FFNレイヤーにおける隠れ層の倍率1。一般的なTransformerでは$4$が多い。

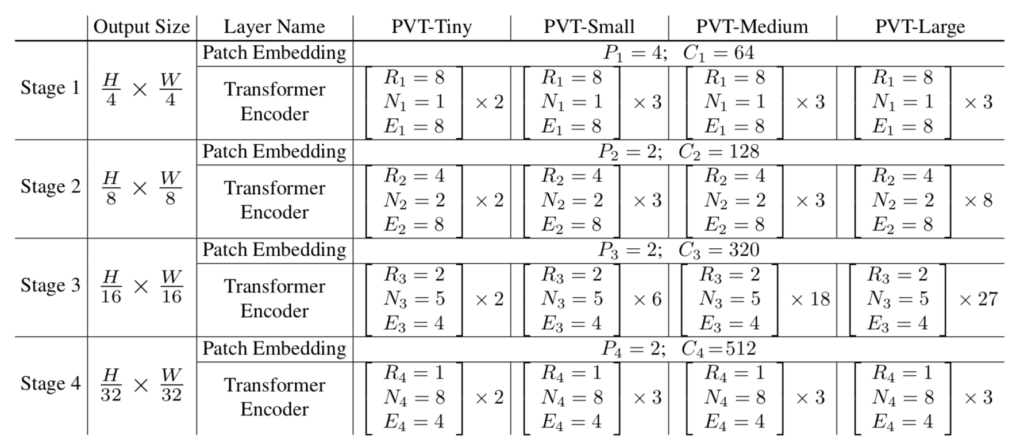
上記のハイパーパラメータと具体的なモデルの対応は下記を元に確認することができます。

Patch embedding

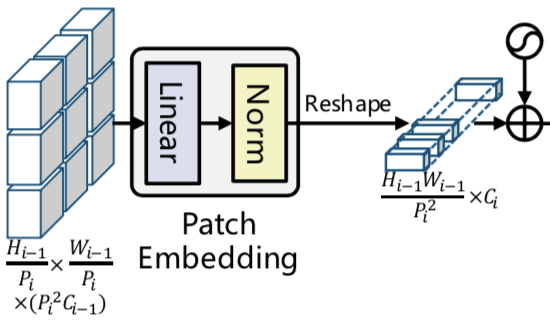
Patch embeddingでは入力画像や$i-1$番目のステージの出力を元に$i$番目のステージにおける入力の調整を行います。
$$
\large
\begin{align}
H_{i-1} \times W_{i-1} \times C_{i-1}
\end{align}
$$

ステージ$i-1$の出力のサイズは上記のように表されますが、ステージ$i$ではまず始めに近隣パッチを連結することにより、下記のようなサイズのFeature Mapを得ます。
$$
\large
\begin{align}
\frac{H_{i-1}}{P_{i}} \times \frac{W_{i-1}}{P_{i}} \times (P_{i}^{2} C_{i-1}) \quad (1)
\end{align}
$$

上記はステージ$i$ではステージ$i-1$の出力を$P_{i} \times P_{i}$単位でパッチの連結を行い、その分チャネル(TransformerのMLP層のサイズに対応)が増えたと理解できます。

Patch embedding層では$(1)$式における$P_{i}^{2} C_{i-1}$のチャネルに対しMLP処理を行うことで、チャネル数を$C_{i}$に変えます。
$$
\large
\begin{align}
\frac{H_{i-1}}{P_{i}} \times \frac{W_{i-1}}{P_{i}} \times C_{i} \quad (1)’
\end{align}
$$

さらにReshape処理を行うことで下記のようなサイズを持つTransformer encoder層の入力が作成されます。
$$
\large
\begin{align}
\frac{H_{i-1} W_{i-1}}{P_{i}^{2}} \times C_{i}
\end{align}
$$

また、$H_{i-1}, W_{i-1}$と$H_{i}, W_{i}$について下記が成立することも合わせて抑えておくと良いです。
$$
\large
\begin{align}
\frac{H_{i-1}}{P_{i}} &= H_{i} \\
\frac{W_{i-1}}{P_{i}} &= W_{i}
\end{align}
$$

Transformer encoder

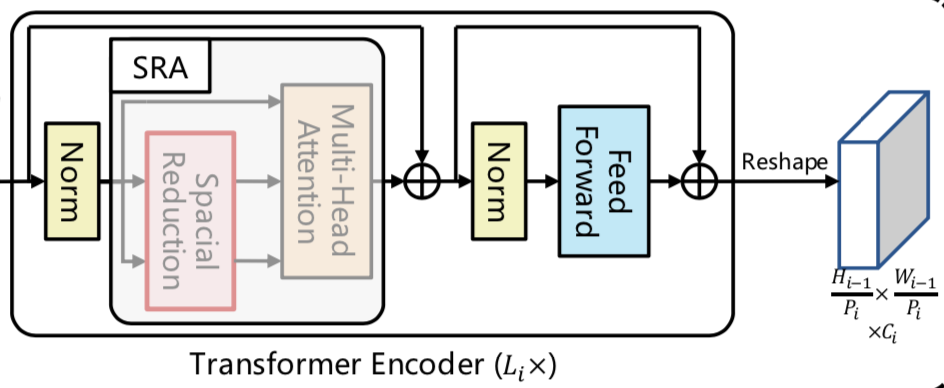
Transformer encoderではPatch embeddingによって作成されたTransformerの入力を元にTransformerの演算が行われます。ステージ$i$では$1$度のPatch embedding処理に対し、$L_i$回のTransformer処理が行われることに注意が必要です。

Spatial Reduction Attention(SRA)はCNNと同様に画像の局所的な相関を活用することで処理の効率化を行う手法です。詳しくは次項で取り扱います。

Spatial Reduction Attention(SRA)

Spatial Reduction Attention(SRA)はAttentionの入力であるKeyとValueの解像度を低くすることで計算の効率化を実現する手法です。

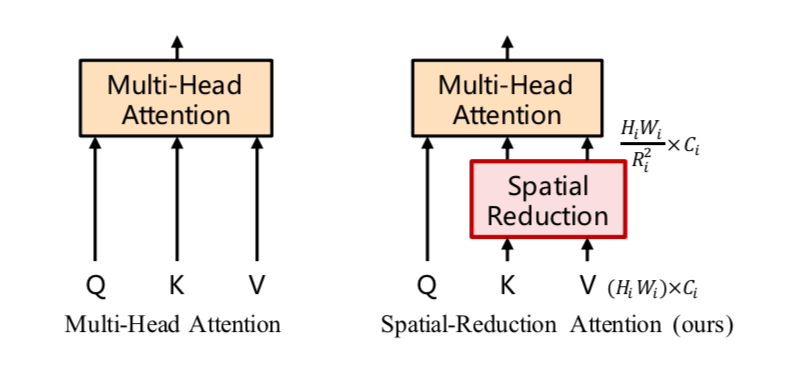
Spatial Reduction Attention処理は下記のような数式で表されます²。
$$
\large
\begin{align}
\mathrm{SRA}(Q, K, V) &= \mathrm{Concat}(\mathrm{head}_{1}, \cdots , \mathrm{head}_{N_{i}})W^{O} \quad (2) \\
\mathrm{head}_{j} &= \mathrm{Attention}(Q W_{j}^{Q}, \mathrm{SR}(K) W_{j}^{K}, \mathrm{SR}(V) W_{j}^{V}) \quad (3) \\
W_{j}^{Q} & \in \mathbb{R}^{C_i \times d_{head}}, \, W_{j}^{K} \in \mathbb{R}^{C_i \times d_{head}}, \, W_{j}^{V} \in \mathbb{R}^{C_i \times d_{head}} \\
W^{O} & \in \mathbb{R}^{C_i \times C_i} \\
d_{head} &= \frac{C_i}{N_i} \quad (4)
\end{align}
$$

$(2)$式は一般的なMultiHead Attentionの計算と同じである一方で、$(3)$式の$\mathrm{head}_{j}$の計算過程に$\mathrm{SR}(K)$が出てくることに注意が必要です。行列$X$についてこの$\mathrm{SR}(X)$の計算は下記のように定義されます。
$$
\large
\begin{align}
\mathrm{SR}(X) &= \mathrm{Norm}(\mathrm{Reshape}(X, R_i)W^{S}) \quad (5) \\
X \in \mathbb{R}^{(H_i W_i) \times C_i}, \,\, & \mathrm{Reshape}(X, R_i) \in \mathbb{R}^{\frac{H_i W_i}{R_i^{2}} \times (R_i^{2} C_i)}, \,\, W^{S} \in \mathbb{R}^{(R_i^{2} C_i) \times C_i} \quad (6)
\end{align}
$$

$\displaystyle \mathrm{Reshape}(X, R_i) \in \mathbb{R}^{\frac{H_i W_i}{R_i^{2}} \times (R_i^{2} C_i)}$で表したように、$(5)$式のReshape処理はPatch embeddingと同様な処理が行われるので対応させて抑えておくと良いと思います。

$(5)$式と$(6)$式より、$\mathrm{SR}(X)$は$\displaystyle \mathrm{SR}(X) \in \mathbb{R}^{\frac{H_i W_i}{R_i^{2}} \times C_i}$で表される行列であり、$X \in \mathbb{R}^{(H_i W_i) \times C_i}$の行数が$\displaystyle \frac{1}{R_i^{2}}$になったことが確認できます。この処理は「Queryに対応して重み付け和を計算するValueの空間方向の解像度を低くすることで、CNNにおけるダウンサンプリングと同様な効果が得られる」と解釈することができます³。

参考

・Transformer論文：Attention is All you need[$2017$]
・Pyramid Vision Transformer論文

1. expansion ratioの厳密な説明が論文内に見当たらなかったので、要出典。 ↩︎
2. 論文では$d_{head}$と表記がありますが、$(4)$式で定義されるようにステージ$i$毎に$d_{head}$の値が変わる可能性があることは注意しておくと良いです。 ↩︎
3. TransformerにおけるAttentionでは$K=V$かつ$Q, K, V$の列数が一致する必要がある一方で、$Q$と$K=V$の行数が必ずしも一致しないことは抑えておくと良いと思います。Encoderでは$Q=K=V$であることが多い一方で、Decoderでは$Q \neq K$の計算も行われます。 ↩︎