TransformerのSelf-Attentionはグラフニューラルネットワーク(GNN)を元に理解することができます。当記事では二部グラフ(bipartite graph)に基づくTransformerのCross-Attentionの理解にあたって取りまとめを作成しました。
・用語/公式解説
https://www.hello-statisticians.com/explain-terms
Contents
前提の確認
グラフ理論とグラフニューラルネットワーク
下記で詳しく取り扱いました。
二部グラフ
グラフ理論における$2$部グラフ(bipartite graph)は「頂点集合を$2$つに分割して各部分の頂点は互いに隣接しないようにできるグラフ1」のことです。
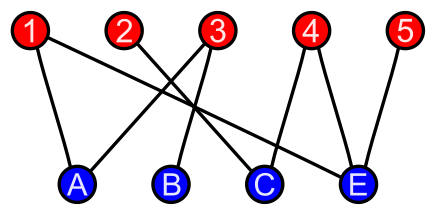
上図のように$2$部グラフでは頂点集合を「赤」と「青」の$2$つに分割し、それぞれのノード間をエッジで連結します。上図のグラフは下図のように表すこともできます。

上図のような表し方に基づいて、「赤と青のそれぞれのノードが交互に出てくるグラフ」のように$2$部グラフを解釈することも可能です。また、赤と青の全てのノードの組み合わせをエッジで連結したグラフを完全$2$部グラフ(complete bipartite graph)といいます。
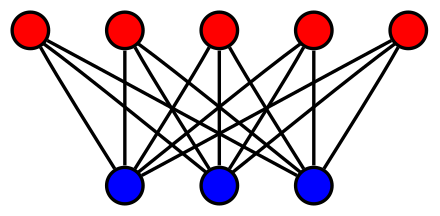
完全$2$部グラフは上図のように表すことができます。上図のように$2$部グラフ・完全$2$部グラフでは$2$つのノード集合の要素数が一致しない場合があります。DeepLearningではMLP(Multi Layer Perceptron)の層間の計算を表した図が完全$2$部グラフに対応することは抑えておくと良いです。
当記事でのメインテーマであるTransformerにおけるCross-Attentionも完全$2$部グラフで表すことができることを次節で確認を行います。
$2$部グラフとCross-Attentionの解釈
Cross-Attentionの概要
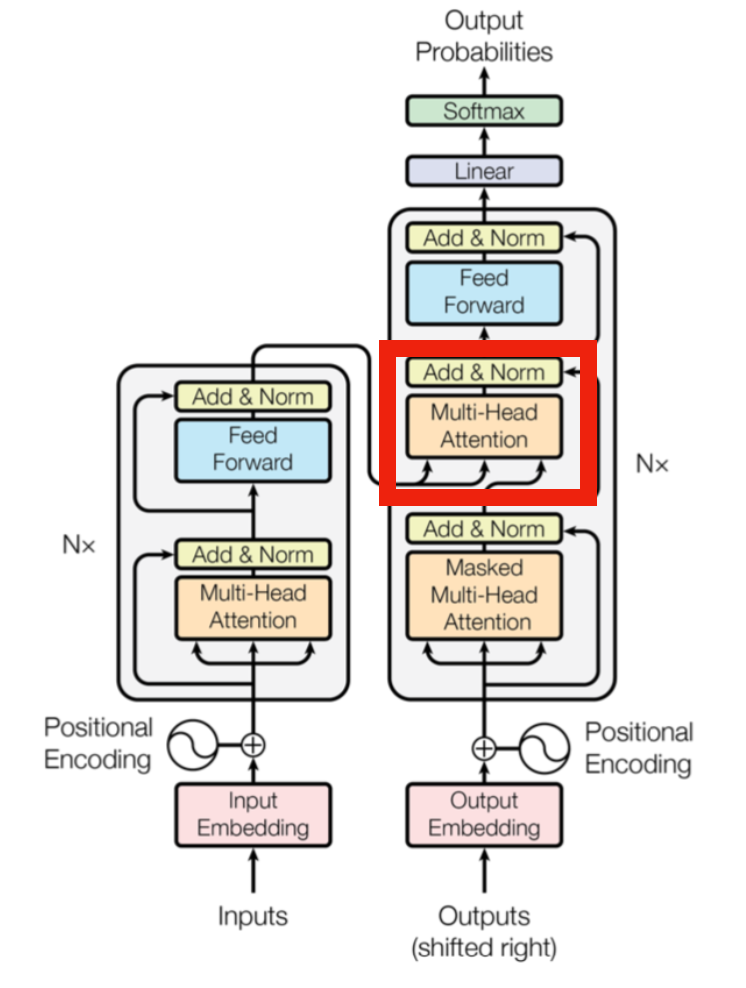
上図の赤枠で示すようにTransformerのDecoderではEncoderからの出力をKey・Value、Decoderへの入力をQueryとするCross-Attentionの処理が行われます。Cross-Attentionの名称は下記などを参考にしました2。

Cross-AttentionはQuery・Key・Valueの用意の仕方がSelf-Attentionと異なる一方で、計算自体は同様なので、それぞれを$Q, K, V$と表すとき下記のような式でCross-Attentionの処理を表すことができます。
$$
\large
\begin{align}
\mathrm{CrossAttention}(Q, K, V) &= \mathrm{softmax} \left( \frac{Q K^{\mathrm{T}}}{\sqrt{d}} \right) V \quad (1) \\
Q & \neq K = V
\end{align}
$$
$2$部グラフとCross-Attentionの対応と処理の解釈
Cross-AttentionはQueryを$1$つ目のノード集合、Key・Valueを$2$つ目のノード集合とする完全$2$部グラフを元に表すことができます。
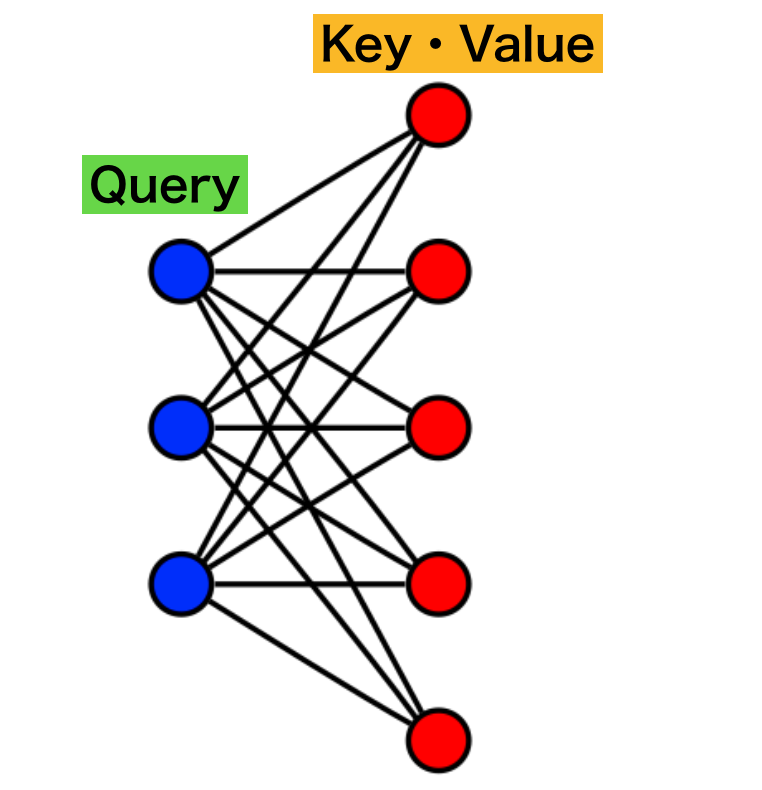
たとえば上図のように「青」のノード集合をQuery、「赤」のノード集合をKey・Valueに対応させ、それぞれのノード間の類似度を計算し、重み付け和を計算することで$(1)$式で表されるCross-Attentionと同様の計算を行うことができます。
TransformerのDecoderにおけるCross-Attention
TransformerのDecoderではCross-AttentionによってDecoderへのそれぞれの入力についてEncoderの出力を反映させます。このような処理に基づいて機械翻訳などに用いられる系列変換タスクや文章生成などを実現することができます。
Key・Valueのダウンサンプリングと計算の軽量化
Cross-AttentionではQueryとKey・Valueが一致する必要がないことから、Key・Valueのノードの数を削減し、計算の軽量化を実現することが可能です。たとえばPVTにおけるSpatial Reduction Attention(SRA)やSegFormerにおけるEfficient Self-Attentionなどが軽量化の例です。
Spatial Reduction Attention(SRA)やEfficient Self-Attentionでは隣接するViTのパッチが局所相関を持つことから局所領域でパッチを連結したものをKey・Valueと見なす手法です。このような処理を行うことでViTの計算量を抑えることが可能になります。
