SimCSE(Simple Contrastive Learning of Sentence Embeddings)は対照学習(Contrastive Learning)を用いてテキストのベクトル表現を抽出する手法です。当記事ではSimCSEの一連の学習手順について取りまとめを行いました。
SimCLRの論文の「SimCSE: Simple Contrastive Learning of Sentence Embeddings」を参考に作成を行いました。
・用語/公式解説
https://www.hello-statisticians.com/explain-terms
前提の確認
指示関数
指示関数(indicator function)の$\mathbb{1}_{[k \neq i]} \in \{ 0, 1 \}$は下記のように定義されます。
$$
\large
\mathbb{1}_{[k \neq i]} =
\begin{cases}
1 \quad \mathrm{if} \quad k \neq i \\
0 \quad \mathrm{otherwise}
\end{cases}
$$
SimCLR
SimCSEはSimCLRと同様に対照学習(Contrastive Learning)という枠組みに基づいて学習が行われます。SimCLRについては下記で詳しく取り扱いました。
SimCSE
SimCSEの全容
SimCSEの全容は下記を元に掴むと良いです。
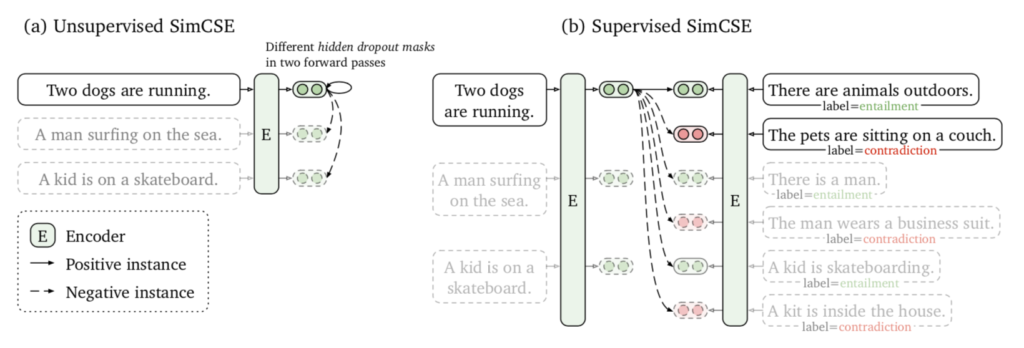
SimCSEは「教師なしCSE(Unsupervised CSE)」と「教師ありCSE(Supervised CSE)」の二つに大別され、上図の$(\mathrm{a})$が教師なしCSE、$(\mathrm{b})$が教師ありCSEにそれぞれ対応します。
次項と次々項でUnsupervised CSEとSupervised CSEについて詳しく確認を行います。
Unsupervised CSE
Unsupervised CSEでは同じ入力テキスト$x_i$をTransformerに$2$度入力し、FFN層で$2$種類のDropout maskの$z_i, z_i’$を作用させることで$2$種類のembeddingである$h_{i}^{z_{i}}, h_{i}^{z_{i}’}$を取得し、学習を行います。
学習にあたっては、SimCLRと同様に入力$x_i$について下記のようなlossの$l_i$を定義し、lossが最小になるようにパラメータの学習を行います。
$$
\large
\begin{align}
l_i &= -\log{ \frac{e^{\mathrm{sim}}(h_{i}^{z_{i}}, h_{i}^{z_{i}’})/\tau}{\sum_{j=1}^{N} e^{\mathrm{sim}}(h_{i}^{z_{i}}, h_{j}^{z_{j}’})/\tau} }
\end{align}
$$
SimSCEではハイパーパラメータであるDropout rateの$p$のデフォルト値が$p=0.1$とされることも合わせて抑えておくと良いです。
Supervised CSE
Supervised CSEではNLI(Natural Language Inference)のデータセットが用いられます。NLIでは対象の一文に対し、絶対的に正しい(entailment)、正しいかもしれない(neutral)、明確に正しくない(contradiction)の$3$つが与えられます。
Supervised CSEでは入力$x_i$に対し、entailmentを正例$x_i^{+}$、contradictionを負例$x_i^{-}$と見なし下記のように定義されるlossの$l_i$を最小化するように学習を行います。
$$
\large
\begin{align}
l_i &= -\log{ \frac{e^{\mathrm{sim}}(h_{i}, h_{i}^{+})/\tau}{\sum_{j=1}^{N} \left( e^{\mathrm{sim}(h_{i}, h_{j}^{+})/\tau} + e^{\mathrm{sim}(h_{i}, h_{j}^{-})/\tau} \right)} }
\end{align}
$$
