クラス活性マッピング(CAM; Class Activation Mapping)はDeepLearningにおける予測に寄与した領域の可視化を行う際に用いる手法です。当記事では特定のネットワーク構造でしか用いることのできないCAMを一般的に用いれるように拡張を行ったGrad-CAMについて取りまとめました。
Grad-CAMの論文である「Grad-CAM: Visual Explanations from Deep Networks via Gradient-based Localization」や「深層学習 第$2$版」第$9$章「説明と可視化」の内容を参考に作成を行いました。
・用語/公式解説
https://www.hello-statisticians.com/explain-terms
前提の確認
クラス活性マッピング
クラス活性マッピング(CAM; Class Activation Mapping)の最もシンプルな例には、下記のようなCNN構造を持つ場合が挙げられます。
(最終畳み込み層、ReLUが活性化関数)$\, \longrightarrow \,$(大域平均プーリング(GAP)層)$\, \longrightarrow \,$(ソフトマックス関数)$\, \longrightarrow \,$(クラススコア)
上記のような場合、最終畳み込み層の出力のFeature mapを$A \in \mathbb{R}^{H \times W \times C}$とすると、ReLUによって$Z$の全ての成分について$A_{ijc} \geq 0$が成立することからFeature mapのチャネル方向の$k$番目を$A_{k} \in \mathbb{R}^{H \times W}$とおくと、$A_{k}$の平均がソフトマックス関数の入力となります。よって、$A_{k}$の可視化を行うことでクラス$k$の分類にどの領域が寄与しているかの確認ができます。
また、CAMは下記のようなネットワーク構造を持つ場合も行うことができます。
(最終畳み込み層、ReLUが活性化関数)$\, \longrightarrow \,$(GAP層)$\, \longrightarrow \,$($1$層の全結合層)$\, \longrightarrow \,$(ソフトマックス関数)$\, \longrightarrow \,$(クラススコア)
上記のようなネットワークの場合、チャネル$c$からクラス$k \in \{ 1, 2, \cdots , K \}$への全結合層のパラメータを$w_{ck}$とおくと、クラス$k$についてのクラス活性$L_{\mathrm{CAM}}^{k}$は下記のように計算できます1。
$$
\large
\begin{align}
L_{\mathrm{CAM}}^{k} = \sum_{c=1}^{C} w_{ck} Z_{c}
\end{align}
$$
Grad-CAM
Grad-CAMの概要・数式
Grad-CAMの処理の全体像は下図を元に掴むと良いです。
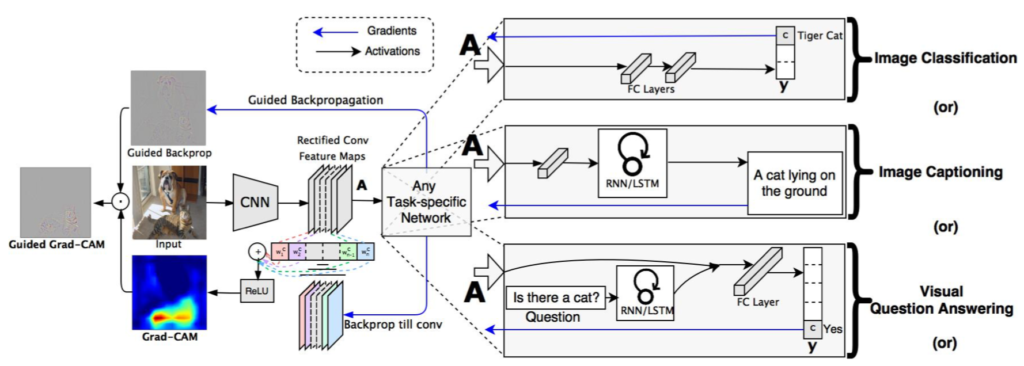
Grad-CAMに基づくクラス$k$のクラス活性$L_{\mathrm{Grad-CAM}}^{k} \in \mathbb{R}^{H \times W}$はFeature mapの$A^{c}, \, c = 1, \cdots C$、クラス$k \in \{ 1, 2, \cdots , K \}$のソフトマックスへの入力値$y^{k}$を元に下記のように定義されます。
$$
\large
\begin{align}
L_{\mathrm{Grad-CAM}}^{k} &= \mathrm{ReLU} \left( \sum_{c=1}^{C} \alpha_{c}^{k} A^{c} \right) \\
\alpha_{c}^{k} &= \frac{1}{HW} \sum_{i=1}^{H} \sum_{j=1}^{W} \frac{\partial y^{k}}{\partial A_{ij}^{c}}
\end{align}
$$
Grad-CAMは上記のように偏微分の計算に基づいてCAM(Class Activation Mapping)の一般化を行う手法です。
参考
- Grad-CAMの論文ではFeature mapのインデックスが$k$、クラス分類のインデックスが$c$で表されますが、「$K$クラス分類問題」や「チャネル数$C$」などのように表されることが多いので当記事では逆に用いました。 ↩︎
