点群にDeepLearningを導入したPointNetは有力な手法である一方で、max poolingを一度しか行わないことで局所的な構造をなかなか抽出できないという課題があります。当記事ではこの解決にあたって階層化グルーピングを用いた研究であるPointNet++について取りまとめを行いました。
PointNet++の論文である「PointNet++: Deep Hierarchical Feature Learning on Point Sets in a Metric Space」の内容を参考に作成を行いました。
・用語/公式解説
https://www.hello-statisticians.com/explain-terms
Contents
前提の確認
PointNet
PointNet++
処理の概要
PointNet++の処理の全体像は下図を元に掴むと良いです。
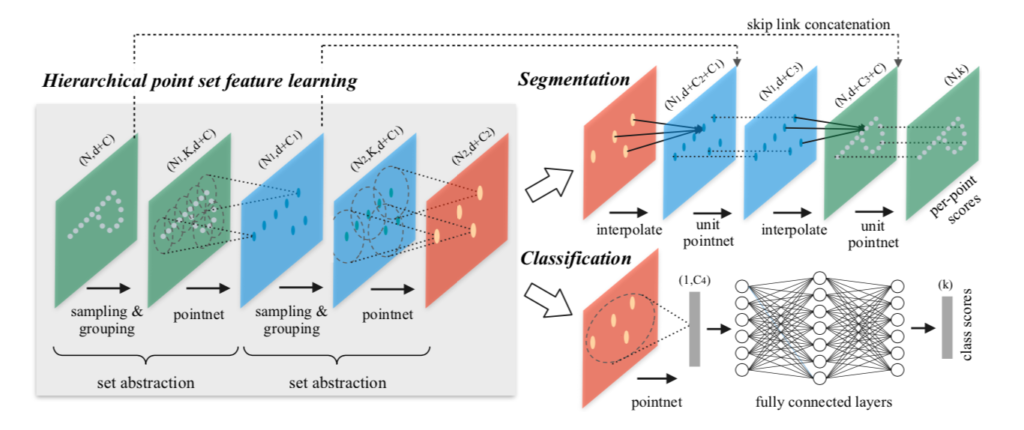
上図から確認できるように、PointNet++はVGGNetやResNetにおけるbackbone処理とタスク特化処理の二つによって大まかに構成されます。
backbone処理ではSet Abstraction、SegmentationタスクではFeature Propagationをそれぞれ理解すると良いです。Set Abstractionは次項、Feature Propagationについては次々項でそれぞれ詳しく取り扱いました。
Set Abstraction
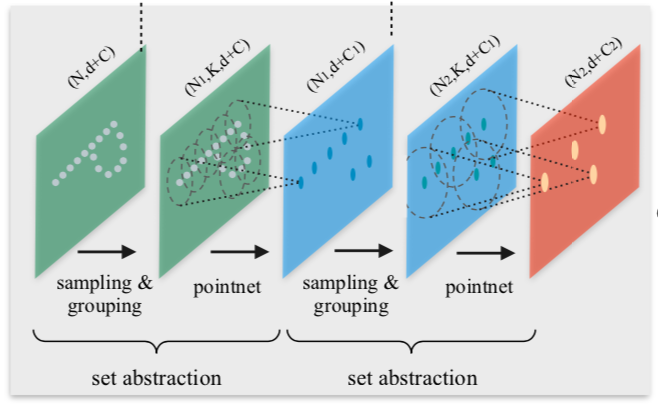
上図から確認できるように、Set Abstractionは以下の$3$つのkey layerで構成されます。
・Sampling layer
・Grouping layer
・PointNet layer
上記の$3$つのlayerは、「Sampling layer」で局所領域における中心点(centroid)を決め、「Grouping layer」で局所領域における中心点の近傍にある点をグルーピングし、「PointNet layer」でグルーピングした点の集合から特徴量の抽出を行う、とそれぞれ解釈すると良いです。PointNet論文ではこの$3$つのkey layerの処理をまとめてset abstractionと表しており、Figure$\, 2$でもset abstractionの記載が確認できます。
以下、「Sampling layer」、「Grouping layer」、「PointNet layer」のそれぞれについて詳しく確認を行います。
Sampling layer
Sampling layerでは$N$個の点集合$\{ x_1, \cdots , x_{N} \}$に対しFPS(farthest point sampling)を行うことで、$N’$個の点集合$\{ x_{i_{1}}, \cdots , x_{i_{N’}} \}$をの抽出を行います。
ここで$i_{j}$は順序$i$1の$j$番目に対応するインデックスを表します2。ここでFPSは$x_{i_{j}}$の選定にあたって、$j-1$の点集合$\{ x_{i_{1}}, \cdots , x_{i_{j-1}} \}$から最も遠い点を選択する手法であると理解すると良いです。
中心点(centroid)の選択にあたってはランダムサンプリングも可能ですが、定数$K$が固定されるときFPSを用いることでより全体の点集合をカバーすることができるなど有用です。FPSを用いたこのような処理はCNNにおけるreceptive fieldと対応させて解釈すると良いです。
Grouping layer
$N$個の点群のそれぞれの点の位置情報が$d$次元、特徴量が$C$次元で表されるとき、これらをまとめて$x_{i} \in \mathbb{R}^{1 \times (d+C)}$のように表せると仮定します。このとき、下記が成立します。
$$
\large
\begin{align}
\left( \begin{array}{c} x_1 \\ \vdots \\ x_N \end{array} \right) & \in \mathbb{R}^{N \times (d+C)} \\
\left( \begin{array}{c} x_{i_{1}} \\ \vdots \\ x_{i_{N’}} \end{array} \right) & \in \mathbb{R}^{N’ \times (d+C)}
\end{align}
$$
ここで$j$番目の中心点(centroid)である$x_{i_{j}}$から半径$R$以内の点のインデックスの集合を$\{ \sigma_{1}, \sigma_{2}, \cdots , \sigma_{K_{j}} \}$とおくと、このインデックスに基づく行列のサイズは下記のように表すことができます3。
$$
\large
\begin{align}
\left( \begin{array}{c} x_{\sigma_{1}} \\ \vdots \\ x_{\sigma_{K_{j}}} \end{array} \right) & \in \mathbb{R}^{K_{j} \times (d+C)} \quad (1)
\end{align}
$$
Grouping layerでは$j$番目の中心点に対し、半径$R$の点を$(1)$式のように抽出を行います。ここで注意が必要なのが「半径$R$」を定義するには計量空間(metric space)が定義される必要があるということです。
計量空間(metric space)には「$\mathbb{R}^{n}$の標準内積」に基づいて定義される計量空間を用いることが一般的で、論文のSection$4.1$のEuclidean Metric Spaceに対応します。
一方でSection$4.3$のようにNon-Euclidean Metric Spaceを用いる場合もあります。
PointNet layer
PointNet layerではそれぞれのグループに対し、PointNetの処理が実行されます。PointNetに$(1)$式を入力した際に$x’_{j} \in \mathbb{R}^{1 \times (d+C’)}$が出力されます。$N’$個の全てのグループについての特徴量は下記のような行列で表されます。
$$
\large
\begin{align}
\left( \begin{array}{c} x’_1 \\ \vdots \\ x’_j \\ \vdots \\ x’_N \end{array} \right) & \in \mathbb{R}^{N’ \times (d+C’)}
\end{align}
$$
Grouping layerで各中心点ごとにサンプル数が可変長になったものをPointNet layerでmax poolingを行うことで固定長に戻すことができることは注意して抑えておくと良いと思います。
Feature Propagation
Feature PropagationはSegmentationタスクを解くにあたって用いられる処理の仕組みです。

上図から確認できるように、プーリングによってダウンサンプリングされた結果をアップサンプリングすることでセグメンテーションタスクの予測が行われます。アップサンプリング時の点の復元にあたっては、$N_{1} \geq N_{2} \geq \cdots N_{l-1} \geq N_{l} \geq \cdots$のようにダウンサンプリングした点を逆に辿って復元を行います。$N_{l}$から$N_{l-1}$の復元にあたっては位置情報を持つ$d$次元はダウンサンプリング時のものをそのまま保持しておき、特徴量の値は補間(interpolation)処理に基づいて取得します。
PointNet++で用いられる補間処理は下記で表した$k$近傍($k$-nearest neighbors)の加重平均の式で定義されます。
$$
\large
\begin{align}
f^{(j)}(x) &= \frac{\sum_{i=1}^{k} w_{i}(x) f_{i}^{(j)}}{\sum_{i=1}^{k} w_{i}(x)}, \, j=1, \cdots , C \quad (2) \\
w_{i}(x) &= \frac{1}{d(x, x_i)^{p}}
\end{align}
$$
上記の式は点$x$の$j$番目の特徴量を$^{(j)}(x)$とおくとき、Centroidの$x_i$との近さに基づいて特徴量を加重平均によって得ると解釈すれば良いです。ここでは論文の表記に合わせて$j$番目の要素について式定義した一方で、$C$次元のベクトルと見なして定義しても良いと思います。また、$d$は$x$と$x_i$のdistanceを意味しており、$p$は次元を表します。補間処理に用いる近傍点の数$k$と次元の$p$については$k=3$、$p=2$がデフォルトで用いられます。
次に、上記のように行う補間処理は一度ダウンサンプリングしたものを用いると高周波成分が消失する場合があり得るので、U-Netのように対応するSet Abstractionのレイヤーの特徴量の反映処理が行われます。この処理はskip link concatenationのように表されます。skip link concatenationについては基本的にはU-Netと同じ仕組みだと理解すると良いと思います。このような処理が行われることから、Feature Propagationの数はSet Abstractionの数と原則一致することも合わせて抑えておくと良いです。
各領域における点の密度の取り扱い
点群における各点は一様分布に基づいていないので、領域ごとに密度の偏りがあります。密(dense)な領域に基づいて学習した結果が疎(sparse)な領域にそのまま一般化することはできないので注意が必要です。
各領域の点の密度の取り扱いにおける「半径$R$を用いる」アプローチの改良にあたって、PointNet++では「MSG(Multi-scale grouping)」と「MRG(Multi-resolution grouping)」の二つの手法が紹介されています。以下それぞれについて詳しく確認します。
Multi-scale grouping
MSG(Multi-scale grouping)は同一の中心点(centroid)に対し、複数のスケールを用いてグルーピングを行う手法です。
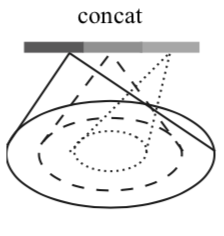
上図には三つのグレースケールがありますが、濃淡と半径$R$の大きさが対応します。計算の詳細についてはPointNet++論文のAppendix.B.$1$のNetwork Architecturesを確認すると良いです。

上記には同じ$R$のみを用いるSSG(Single-Scale Grouping)と複数の$R$を用いるMSG(Multi-scale grouping)の$2$つのネットワーク構造について記載があります。$\mathrm{SA}$、$\mathrm{FC}$やそれぞれのハイパーパラメータについては下記にまとめました。
| 記号 | 意味 |
|---|---|
| $\mathrm{SA}(K, r, [l_{1}, \cdots , l_{d}])$ | SSGにおけるset abstractionの演算。$K$は「中心点/局所領域」の数、$r$はグルーピングの際の半径、$d$はPointNetの層の数、$l_i$は$i$番目の層における出力層の次元を表す。 |
| $\mathrm{SA}([l_{1}, \cdots , l_{d}])$ | max poolingを伴うglobal set abstractionの演算。 |
| $\mathrm{SA}(K, [r^{(1)}, \cdots , r^{(m)}], [[l_{1}^{(1)}, \cdots , l_{d}^{(1)}], \cdots , [l_{1}^{(m)}, \cdots , l_{d}^{(m)}]])$ | MSGにおけるset abstractionの演算。$m$は半径のスケールの数、$r^{(j)}$は$j$番目のスケールにおける半径、$l_{i}^{(j)}$は$j$番目のスケールの$i$番目の層における出力層の次元を表す。 |
| $\mathrm{FC}(l, dp)$ | 全結合(Fully Connected)層の演算、MLPと同義。$l$は出力層の次元、$dp$はDropoutの比率を表す。 |
| $\mathrm{FP}(l_1, \cdots , l_{d})$ | feature propagation層 |
上記の表を元に「PointNet++論文 Appendix.B.$1$ Network Architectures」を確認すると、SSGによる分類では$K=512, r=0.2$で$64 \to 64 \to 128$のMLP演算が行われたのちに、$K=128, r=0.4$で$128 \to 128 \to 256$のMLP演算が行われることが読み取れます。さらにこの後Globalにmax poolingを実行し、$256 \to 256 \to 512$でMLP処理を行い、$512$次元のベクトルに対し全結合層の計算を何度か実行したのちに$K$クラス分類問題に用いる$K$次元のベクトルを出力することが読み取れます。
上記と同様にMSGの処理も読み取ることができます。
Multi-resolution grouping
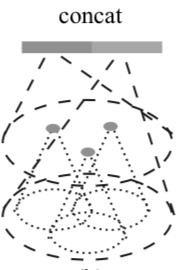
参考
- たとえば$N=5$、$i_{1}=2, i_{2}=5, i_{3}=4, i_{4}=1, i_{5}=3$のとき、$N’=3$であれば$\{ x_{i_{1}}, \cdots , x_{j_{N’}} \}$は$\{ x_2, x_5, x_4 \}$に対応します。 ↩︎
- 文字$i$はインデックスに用いられることが多いので紛らわしいですが、PointNet++論文で$i$が用いられているのでそのまま用いました。また、論文の$n, m$についてはGrouping layerと対応させるにあたって当記事では$N, N’$で置き換えました。 ↩︎
- PointNet++の論文では$N’$個の中心点に対し、$N’ \times K \times (d+C)$のように定義されますが、$K$が中心点のインデックスに対し定数ではなく可変であり紛らわしいので、当記事では$j$番目の中心点について式定義を行いました。 ↩︎

[…] 【PoinNet++論文まとめ】階層化グルーピングによるPointNetの改良 […]