【Transformer】LLM(Large Language Model)のパラメータ数の概算法

昨今LLM(Large Language Model)が大きな注目を集める一方で、パラメータ数がどのように決まるかについて抑えておくと理解に役立ちます。そこで当記事ではLLMの主要モジュールであるTransformerに用いられるパラメータの概算法について取りまとめを行いました。
Transformerの論文や筆者作成の『直感的に理解するTransformer』の内容などを元に取りまとめを行いました。

・用語/公式解説
https://www.hello-statisticians.com/explain-terms

・Transformer論文
・直感的に理解するTransformer(運営者作成)

パラメータ数の概算

パラメータ数の単位

LLM(Large Language Model)関連の論文ではパラメータ数はMillionを表すMやBillionを表すBで略記されるので注意が必要です。Millionは$10^{6}$の$100$万、Billionは$10^{9}$の$10$億にそれぞれ対応します。

具体的な論文とパラメータ数の対応については、$110$Mと$340$MのBERTが$1.1$億と$3.4$億、$11$BのT$5$が$110$億、$175$BのGPT$3$が$1750$億にそれぞれ対応します。

Transformerの大まかな仕組み

LLMの基盤のアーキテクチャには基本的にTransformerが用いられます。よって、LLMのパラメータ数について解釈する際はTransformerの大まかな仕組みの理解が重要です。Transformerの大まかな仕組みについては下記で詳しくまとめました。

・直感的に理解するTransformer

ネットワーク分析から直感的に理解するTransformerの仕組みと処理の流れ

パラメータ数の概算

Transformerにおけるパラメータは主にEmbedding、各層におけるMulti-Head Attention、FFN(Feed Forward Network)処理にそれぞれ用いられます。下図の赤枠がパラメータ処理に対応します。

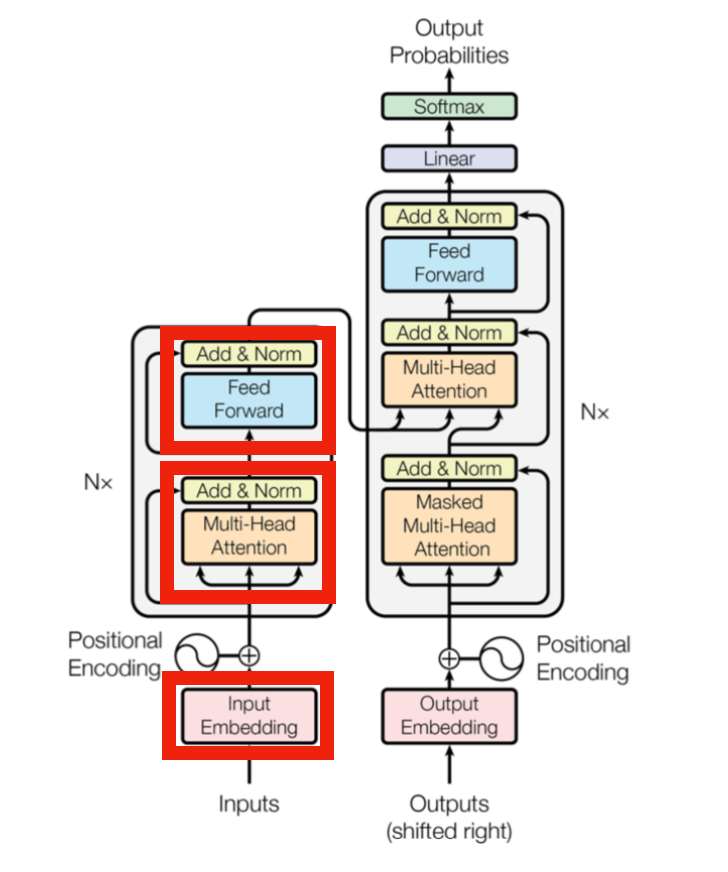
上記に基づいてTransformerに用いられるパラメータ数を大まかに概算することが可能です。以下、パラメータ数の計算を下記の三つにわけて概算します。

$1. \,$ Embedding処理
$2. \,$ Multi-Head Attention処理
$3. \,$ FFN処理

Embedding処理

Embedding処理は$1$-hotベクトルにEmbedding Matrixを左からかけることで得ることができます。このEmbedding Matrixのパラメータ数は語彙数$V$とTransformer処理における隠れ層の数$D$によって概算が可能です。

たとえば$1$万種類の単語に対し、Transformerのそれぞれの単語の隠れ層の数が$D=512$である場合、パラメータ数は下記のように概算できます。
$$
\large
\begin{align}
V \times D &= 10^{4} \times 512 \\
&= 5.12 \times 10^{6}
\end{align}
$$

上記は約$5$Mに対応します。同様に$10$万種類の単語を$D=1024$で取り扱う場合は下記のように概算できます。
$$
\large
\begin{align}
V \times D &= 10^{7} \times 1024 \\
&= 1.024 \times 10^{8}
\end{align}
$$

上記は約$100$Mに対応します。パラメータ数の概算にあたっては、桁数で大まかに把握できるので、$5.12 \times 10^{6}$や$1.024 \times 10^{8}$のようにパラメータ数を表しました。

トークンが単語単位の場合はWord$2$vecがEmbeddingに対応する一方で、トークンの種類が増大するLLMではBPE(Byte Pair Encoding)などを用いることで$3$万〜$7$万種程度の語彙(vocabulary)に集約させるのが一般的です。よって、LLMの学習時に取り扱う文章が増えても語彙数は数万程度に収まることが多いです。

Multi-Head Attention処理

$$
\large
\begin{align}
\mathrm{MultiHead}(Q,K,V) &= \mathrm{Concat}(\mathrm{head}_{1}, \cdots , \mathrm{head}_{h}) W^{O} \\
\mathrm{head}_{i} &= \mathrm{Attention}(QW_{i}^{Q}, KW_{i}^{K}, VW_{i}^{V}) \\
W_{i}^{O} \in \mathbb{R}^{hd_{v} \times d_{model}}, \, W_{i}^{Q} & \in \mathbb{R}^{d_{model} \times d_{k}}, \, W_{i}^{K} \in \mathbb{R}^{d_{model} \times d_{k}}, W_{i}^{V} \in \mathbb{R}^{d_{model} \times d_{v}}
\end{align}
$$

Multi-Head Attentionではアンサンブル学習と同様に各Headにおける計算の相関が低くなるようにパラメータ$W$を元に上記のような計算を行います。ここで$d_{model}$は各トークンの分散表現の次元数であり前項の$D$と同義です。また、$h$はヘッドの数を表します。このとき、パラメータ数は下記のように概算できます。
$$
\large
\begin{align}
N \times d_{model} \times (h \times (2d_{k} + d_{v}) + h d_{v}) = 2 N d_{model} h(d_{k}+d_{v}) \quad (1)
\end{align}
$$

$N=6, d_{model}=512, h=8, d_{k}=64, d_{v}=64$のとき、Multi-Head Attention処理のパラメータ数は$(1)$式を元に下記のように概算できます。
$$
\large
\begin{align}
2 N d_{model} h(d_{k}+d_{v}) &= 2 \times 6 \times 512 \times 8 \times (64+64) \\
&= 6291456 = 6.29 \times 10^{6}
\end{align}
$$

上記は$6.29$Mに対応します。

FFN処理

FFN処理は単語ごとの隠れ層に対してMLP(Multi Layer Perceptron)を行うことに対応します。よって、単語数$L$、それぞれの単語の隠れ層の数が$D$である場合、$N$層のMLPにおけるパラメータ数は下記のように概算することができます。
$$
\large
\begin{align}
N \times L \times D^{2} = NLD^2
\end{align}
$$

たとえば、$N=6, L=512, D=512$の場合、パラメータ数は下記のように概算できます。
$$
\large
\begin{align}
6 \times 512 \times 512^2 &= 805306368 \\
& \simeq 8.53 \times 10^{8}
\end{align}
$$

上記は$800$Mに対応し、Transformerのパラメータ数の約$100$Mを大きく上回ります。Transformerでは一般的に同じ層の単語では同じパラメータを使うので、$L$はかけないことに注意が必要です。また、FFNの処理では「$D$次元$\to$$D$次元」ではなく、「$D$次元$\to$$4D$次元$\to$$D$次元」のような処理が行われます。中間層の$4D$は別途設定されることもありますが、$4D$が用いられることが多いです。ここまでの内容に基づいてFFN処理におけるパラメータは下記のように概算できます。
$$
\large
\begin{align}
2 \times N \times D \times 4D = 8ND^2 \quad (2)
\end{align}
$$

また、$N=6, D=512$の場合のパラメータ数は$(2)$式より下記のように概算できます。
$$
\large
\begin{align}
8ND^2 &= 8 \times 6 \times 512^{2} \\
&= 12582912 = 1.26 \times 10^{7}
\end{align}
$$

上記は$12.6$Mに対応します。

LLMのパラメータ数の概算

注意事項：Encoder-Decoderの場合

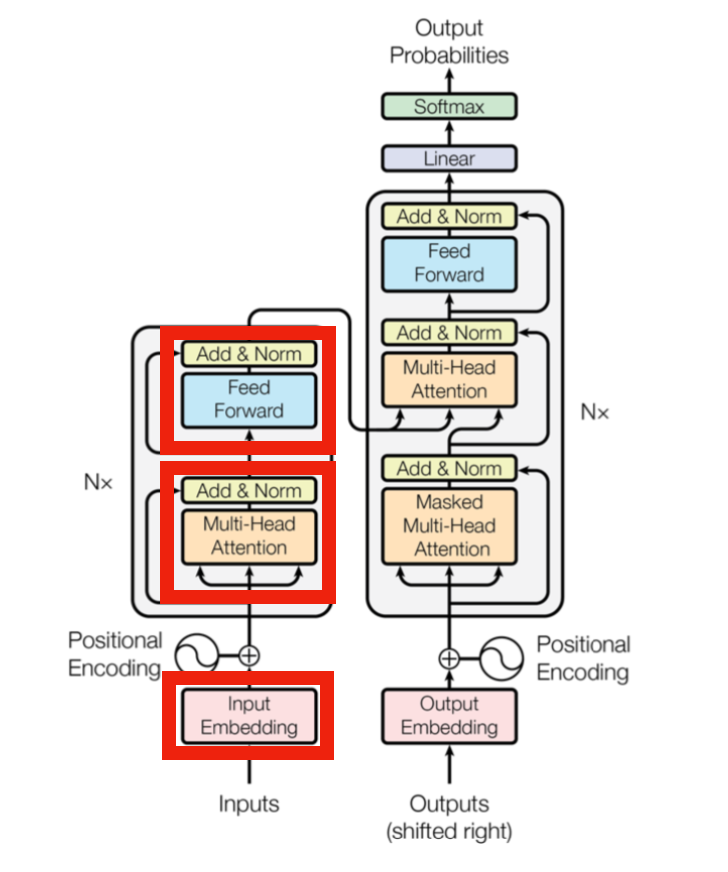
前節では上図を元にEncoder部分のみを確認しましたが、論文によってEncoderとDecoderの双方を用いる場合があることに注意が必要です。この場合、Multi-Head Attentionのパラメータ数を$3$倍、FFNの処理のパラメータ数を$2$倍して概算する必要があります。

具体的にはTransformerの論文やT$5$の論文はEncoderとDecoderを用いており、BERTやGPT-$3$は片方のみが用いられます。

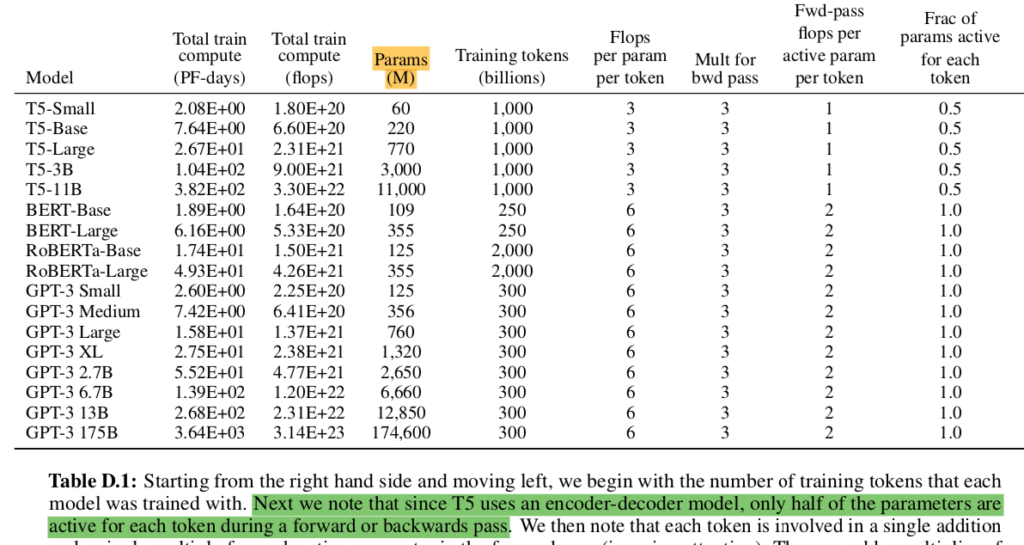
上記はGPT-$3$の論文のTable$D.1$に対応しますが、「T$5$がencoder-decoder modelであるのでパラメータの半数のみがactive」というような注意書きが読み取れます。

このように論文毎にパラメータの概算方法が変わる場合があるので単にパラメータの総数だけでなく、大まかな概算法も合わせて抑えておくと良いです。

Transformer

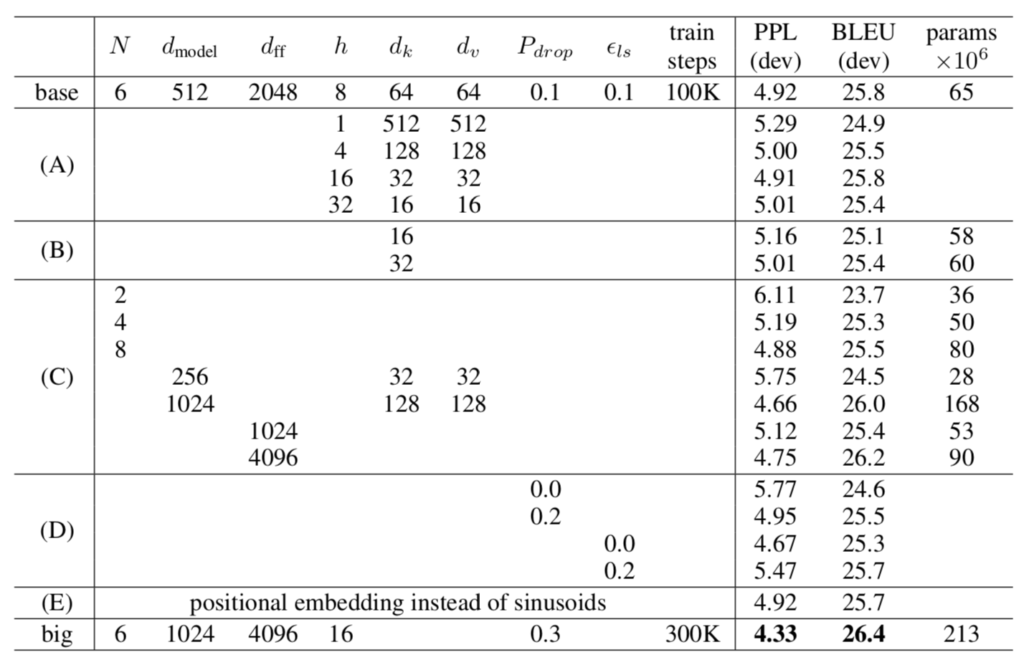
Transformer論文のパラメータ設定は上記より確認できます。以下、Transformerのパラメータ数がEncoder-Decoderを前提に計算されることを元にbaseとbigの双方についてパラメータの概算を行います。

base

・Embedding
$V=37000, D=512$を元にパラメータ数は下記のように計算できます。
$$
\large
\begin{align}
V \times D &= 37000 \times 512 \\
&= 18{,}944{,}000
\end{align}
$$

・Multi-Head Attention
$N=6, d_{model}=512, h=8, d_{k}=64, d_{v}=64$を元にパラメータ数は下記のように計算できます。
$$
\large
\begin{align}
2 N d_{model} h(d_{k}+d_{v}) \times 3 &= 2 \times 6 \times 512 \times 8 \times (64+64) \times 3 \\
&= 18{,}874{,}368
\end{align}
$$

・FFN
$N=6, D=512$の場合のパラメータ数は下記のように概算できます。
$$
\large
\begin{align}
8ND^2 \times 2 &= 8 \times 6 \times 512^{2} \times 2 \\
&= 25{,}165{,}824
\end{align}
$$

よって、パラメータの総数は下記のように概算できます。
$$
\large
\begin{align}
& 18{,}944{,}000 + 18{,}874{,}368 + 25{,}165{,}824 \\
&= 62{,}984{,}192 = 6.3 \times 10^{7}
\end{align}
$$

上記は$63$Mなので、表の値と概ね一致することが確認できます。

big

・Embedding
$V=37000, D=1024$を元にパラメータ数は下記のように計算できます。
$$
\large
\begin{align}
V \times D &= 37000 \times 1024 \\
&= 37{,}888{,}000
\end{align}
$$

・Multi-Head Attention
$N=6, d_{model}=1024, h=16, d_{k}=64, d_{v}=64$を元にパラメータ数は下記のように計算できます。
$$
\large
\begin{align}
2 N d_{model} h(d_{k}+d_{v}) \times 3 &= 2 \times 6 \times 1024 \times 16 \times (64+64) \times 3 \\
&= 75{,}497{,}472
\end{align}
$$

・FFN
$N=6, D=1024$の場合のパラメータ数は下記のように概算できます。
$$
\large
\begin{align}
8ND^2 \times 2 &= 8 \times 6 \times 1024^{2} \times 2 \\
&= 100{,}663{,}296
\end{align}
$$

よって、パラメータの総数は下記のように概算できます。
$$
\large
\begin{align}
& 37{,}888{,}000 + 75{,}497{,}472 + 100{,}663{,}296 \\
&= 214{,}048{,}768 = 2.14 \times 10^{8}
\end{align}
$$

上記は$214$Mなので、表の値と概ね一致することが確認できます。

BERT

BERT論文のパラメータ設定は上記より確認できます。以下、BERTのパラメータ数がEncoderのみを用いて計算されることを元にBASEとLARGEの双方についてパラメータの概算を行います。

BASE

・Embedding
$H=768$がhidden sizeであるので$V=30000, D=768$を元にパラメータ数は下記のように計算できます。
$$
\large
\begin{align}
V \times D &= 30000 \times 768 \\
&= 23{,}040{,}000
\end{align}
$$

・Multi-Head Attention
$N=12, d_{model}=768, h=12, d_{k}=64, d_{v}=64$を元にパラメータ数は下記のように計算できます。
$$
\large
\begin{align}
2 N d_{model} h(d_{k}+d_{v}) &= 2 \times 12 \times 768 \times 12 \times (64+64) \\
&= 28{,}311{,}552
\end{align}
$$

・FFN
$N=12, D=768$を元にパラメータ数は下記のように概算できます。
$$
\large
\begin{align}
8ND^2 &= 8 \times 12 \times 768^{2} \\
&= 56{,}623{,}104
\end{align}
$$

よって、パラメータの総数は下記のように概算できます。
$$
\large
\begin{align}
& 23{,}040{,}000 + 28{,}311{,}552 + 56{,}623{,}104 \\
&= 107{,}974{,}656 = 1.08 \times 10^{8}
\end{align}
$$

上記は$108$Mなので、論文のパラメータ数と概ね一致することが確認できます。

LARGE

・Embedding
$H=1024$がhidden sizeであるので$V=30000, D=1024$を元にパラメータ数は下記のように計算できます。
$$
\large
\begin{align}
V \times D &= 30000 \times 1024 \\
&= 30{,}720{,}000
\end{align}
$$

・Multi-Head Attention
$N=24, d_{model}=1024, h=16, d_{k}=64, d_{v}=64$を元にパラメータ数は下記のように計算できます。
$$
\large
\begin{align}
2 N d_{model} h(d_{k}+d_{v}) &= 2 \times 24 \times 1024 \times 16 \times (64+64) \\
&= 100{,}663{,}296
\end{align}
$$

・FFN
$N=24, D=1024$を元にパラメータ数は下記のように概算できます。
$$
\large
\begin{align}
8ND^2 &= 8 \times 24 \times 1024^{2} \\
&= 201{,}326{,}592
\end{align}
$$

よって、パラメータの総数は下記のように概算できます。
$$
\large
\begin{align}
& 30{,}720{,}000 + 100{,}663{,}296 + 201{,}326{,}592 \\
&= 332{,}709{,}888 = 3.33 \times 10^{8}
\end{align}
$$

上記は$333$Mなので、論文のパラメータ数と概ね一致することが確認できます。

T$5$

T$5$論文のパラメータ設定は上記より確認できます。以下、T$5$のパラメータ数がEncoder-Decoderを前提に計算されることを元に$3B$と$11B$の双方についてパラメータの概算を行います。

$3B$

GPT-$3$

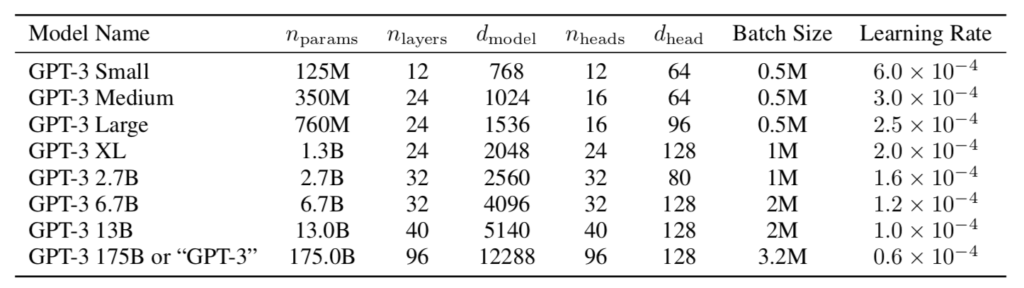
GPT-$3$のパラメータ設定は上記より確認できます。

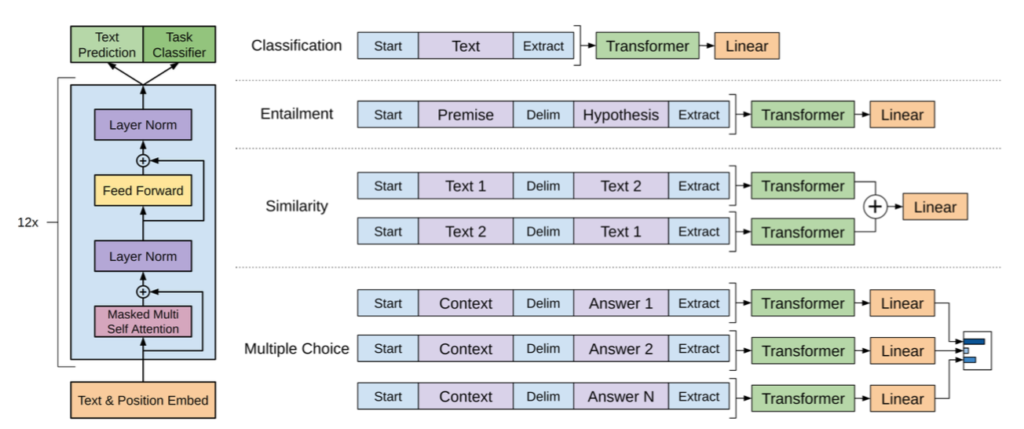
GPT-$3$では上図のようにencoderを用いないTransformerであるTransformer decoderを用います。Transformer decoderの概要については下記で詳しく取り扱いました。

『仕組みから理解するChatGPT』サポートページ【印刷版】

GPT論文のFigure$1$よりGPT-$3$のパラメータ数はencoderのみを用いるBERTと基本的には同様の概算を行えることが確認できます。以下、GPT-$3$のパラメータ数がEncoderのみを用いて計算されることを元に$6.7$B、$13$B、$175$Bについてパラメータの概算を行います。

$6.7$B

・Embedding
$V=40000, D=4096$を元にパラメータ数は下記のように計算できます。
$$
\large
\begin{align}
V \times D &= 40000 \times 4096 \\
&= 163{,}840{,}000
\end{align}
$$

$V=40000$はGPTの論文を参照しました。

・Multi-Head Attention
$N=32, d_{model}=4096, h=32, d_{k}=128, d_{v}=128$を元にパラメータ数は下記のように計算できます。
$$
\large
\begin{align}
2 N d_{model} h(d_{k}+d_{v}) &= 2 \times 32 \times 4096 \times 32 \times (128+128) \\
&= 2{,}147{,}483{,}648
\end{align}
$$

・FFN
$N=32, D=4096$の場合のパラメータ数は下記のように概算できます。
$$
\large
\begin{align}
8ND^2 &= 8 \times 32 \times 4096^{2} \\
&= 4{,}294{,}967{,}296
\end{align}
$$

よって、パラメータの総数は下記のように概算できます。
$$
\large
\begin{align}
& 163{,}840{,}000 + 2{,}147{,}483{,}648 + 4{,}294{,}967{,}296 \\
&= 6{,}606{,}290{,}944 = 6.6 \times 10^{9}
\end{align}
$$

上記は$6.6$Bなので、表の値と概ね一致することが確認できます。

$13$B

・Embedding
$V=40000, D=5140$を元にパラメータ数は下記のように計算できます。
$$
\large
\begin{align}
V \times D &= 40000 \times 5140 \\
&= 205{,}600{,}000
\end{align}
$$

$V=40000$はGPTの論文を参照しました。

・Multi-Head Attention
$N=40, d_{model}=5140, h=40, d_{k}=128, d_{v}=128$を元にパラメータ数は下記のように計算できます。
$$
\large
\begin{align}
2 N d_{model} h(d_{k}+d_{v}) &= 2 \times 40 \times 5140 \times 40 \times (128+128) \\
&= 4{,}210{,}688{,}000
\end{align}
$$

・FFN
$N=40, D=5140$の場合のパラメータ数は下記のように概算できます。
$$
\large
\begin{align}
8ND^2 &= 8 \times 40 \times 5140^{2} \\
&= 8{,}454{,}272{,}000
\end{align}
$$

よって、パラメータの総数は下記のように概算できます。
$$
\large
\begin{align}
& 205{,}600{,}000 + 4{,}210{,}688{,}000 + 8{,}454{,}272{,}000 \\
&= 12{,}870{,}560{,}000 = 1.29 \times 10^{10}
\end{align}
$$

上記は$12.9$Bなので、表の値と概ね一致することが確認できます。

$175$B

・Embedding
$V=40000, D=12288$を元にパラメータ数は下記のように計算できます。
$$
\large
\begin{align}
V \times D &= 40000 \times 12288 \\
&= 491{,}520{,}000
\end{align}
$$

$V=40000$はGPTの論文を参照しました。

・Multi-Head Attention
$N=96, d_{model}=12288, h=96, d_{k}=128, d_{v}=128$を元にパラメータ数は下記のように計算できます。
$$
\large
\begin{align}
2 N d_{model} h(d_{k}+d_{v}) &= 2 \times 96 \times 12288 \times 96 \times (128+128) \\
&= 57{,}982{,}058{,}496
\end{align}
$$

・FFN
$N=96, D=12288$の場合のパラメータ数は下記のように概算できます。
$$
\large
\begin{align}
8ND^2 &= 8 \times 96 \times 12288^{2} \\
&= 115{,}964{,}116{,}992
\end{align}
$$

よって、パラメータの総数は下記のように概算できます。
$$
\large
\begin{align}
& 491{,}520{,}000 + 57{,}982{,}058{,}496 + 115{,}964{,}116{,}992 \\
&= 174{,}437{,}695{,}488 = 1.74 \times 10^{11}
\end{align}
$$

上記は$174$Bなので、表の値と概ね一致することが確認できます。

Gopher

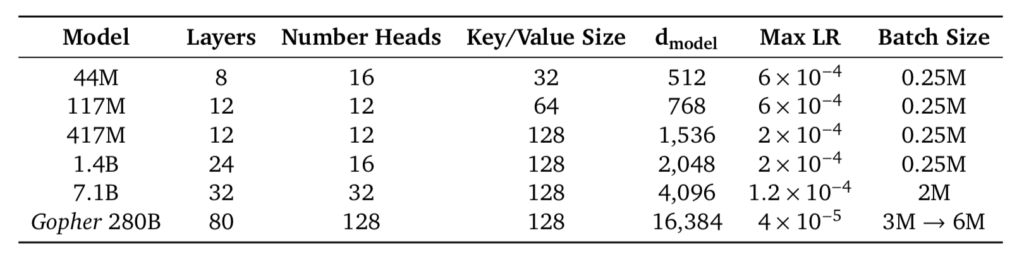
Gopher論文のパラメータ設定は上記より確認できます。基本的にはGPT$3$と同様にTransformer decoderの構成が用いられます。

$44$M

・Embedding
$V=32000, D=512$を元にパラメータ数は下記のように計算できます。
$$
\large
\begin{align}
V \times D &= 32000 \times 512 \\
&= 16{,}384{,}000
\end{align}
$$

・Multi-Head Attention
$N=8, d_{model}=512, h=16, d_{k}=32, d_{v}=32$を元にパラメータ数は下記のように計算できます。
$$
\large
\begin{align}
2 N d_{model} h(d_{k}+d_{v}) &= 2 \times 8 \times 512 \times 16 \times (32+32) \\
&= 8{,}388{,}608
\end{align}
$$

・FFN
$N=8, D=512$の場合のパラメータ数は下記のように概算できます。
$$
\large
\begin{align}
8ND^2 &= 8 \times 8 \times 512^{2} \\
&= 16{,}777{,}216
\end{align}
$$

よって、パラメータの総数は下記のように概算できます。
$$
\large
\begin{align}
& 16{,}384{,}000 + 8{,}388{,}608 + 16{,}777{,}216 \\
&= 41{,}549{,}824 = 4.2 \times 10^{7}
\end{align}
$$

上記は$42$Mなので、表の値と概ね一致することが確認できます。

$117$M

・Embedding
$V=32000, D=512$を元にパラメータ数は下記のように計算できます。
$$
\large
\begin{align}
V \times D &= 32000 \times 768 \\
&= 24{,}576{,}000
\end{align}
$$

・Multi-Head Attention
$N=12, d_{model}=768, h=12, d_{k}=64, d_{v}=64$を元にパラメータ数は下記のように計算できます。
$$
\large
\begin{align}
2 N d_{model} h(d_{k}+d_{v}) &= 2 \times 12 \times 768 \times 12 \times (64+64) \\
&= 28{,}311{,}552
\end{align}
$$

・FFN
$N=12, D=768$の場合のパラメータ数は下記のように概算できます。
$$
\large
\begin{align}
8ND^2 &= 8 \times 12 \times 768^{2} \\
&= 56{,}623{,}104
\end{align}
$$

よって、パラメータの総数は下記のように概算できます。
$$
\large
\begin{align}
& 24{,}576{,}000 + 28{,}311{,}552 + 56{,}623{,}104 \\
&= 109{,}510{,}656 = 1.1 \times 10^{8}
\end{align}
$$

上記は$110$Mなので、表の値と概ね一致することが確認できます。

$417$M

・Embedding
$V=32000, D=1536$を元にパラメータ数は下記のように計算できます。
$$
\large
\begin{align}
V \times D &= 32000 \times 1536 \\
&= 49{,}152{,}000
\end{align}
$$

・Multi-Head Attention
$N=12, d_{model}=1536, h=12, d_{k}=128, d_{v}=128$を元にパラメータ数は下記のように計算できます。
$$
\large
\begin{align}
2 N d_{model} h(d_{k}+d_{v}) &= 2 \times 12 \times 1536 \times 12 \times (128+128) \\
&= 113{,}246{,}208
\end{align}
$$

・FFN
$N=12, D=1536$の場合のパラメータ数は下記のように概算できます。
$$
\large
\begin{align}
8ND^2 &= 8 \times 12 \times 1536^{2} \\
&= 226{,}492{,}416
\end{align}
$$

よって、パラメータの総数は下記のように概算できます。
$$
\large
\begin{align}
& 49{,}152{,}000 + 113{,}246{,}208 + 226{,}492{,}416 \\
&= 388{,}890{,}624 = 3.89 \times 10^{8}
\end{align}
$$

上記は$389$Mなので、表の値と概ね一致することが確認できます。

$1.4$B

・Embedding
$V=32000, D=2048$を元にパラメータ数は下記のように計算できます。
$$
\large
\begin{align}
V \times D &= 32000 \times 2048 \\
&= 65{,}536{,}000
\end{align}
$$

・Multi-Head Attention
$N=24, d_{model}=2048, h=16, d_{k}=128, d_{v}=128$を元にパラメータ数は下記のように計算できます。
$$
\large
\begin{align}
2 N d_{model} h(d_{k}+d_{v}) &= 2 \times 24 \times 2048 \times 16 \times (128+128) \\
&= 402{,}653{,}184
\end{align}
$$

・FFN
$N=24, D=2048$の場合のパラメータ数は下記のように概算できます。
$$
\large
\begin{align}
8ND^2 &= 8 \times 24 \times 2048^{2} \\
&= 805{,}306{,}368
\end{align}
$$

よって、パラメータの総数は下記のように概算できます。
$$
\large
\begin{align}
& 65{,}536{,}000 + 402{,}653{,}184 + 805{,}306{,}368 \\
&= 1{,}273{,}495{,}552 = 1.27 \times 10^{9}
\end{align}
$$

上記は$1.27$Bなので、表の値と概ね一致することが確認できます。

$7.1$B

・Embedding
$V=32000, D=4096$を元にパラメータ数は下記のように計算できます。
$$
\large
\begin{align}
V \times D &= 32000 \times 4096 \\
&= 131{,}072{,}000
\end{align}
$$

・Multi-Head Attention
$N=32, d_{model}=4096, h=32, d_{k}=128, d_{v}=128$を元にパラメータ数は下記のように計算できます。
$$
\large
\begin{align}
2 N d_{model} h(d_{k}+d_{v}) &= 2 \times 32 \times 4096 \times 32 \times (128+128) \\
&= 2{,}147{,}483{,}648
\end{align}
$$

・FFN
$N=32, D=4096$の場合のパラメータ数は下記のように概算できます。
$$
\large
\begin{align}
8ND^2 &= 8 \times 24 \times 2048^{2} \\
&= 4{,}294{,}967{,}296
\end{align}
$$

よって、パラメータの総数は下記のように概算できます。
$$
\large
\begin{align}
& 131{,}072{,}000 + 2{,}147{,}483{,}648 + 4{,}294{,}967{,}296 \\
&= 6{,}573{,}522{,}944 = 6.57 \times 10^{9}
\end{align}
$$

上記は$6.57$Bなので、表の値と概ね一致することが確認できます。

$280B$

・Embedding
$V=32000, D=16384$を元にパラメータ数は下記のように計算できます。
$$
\large
\begin{align}
V \times D &= 32000 \times 16384 \\
&= 524{,}288{,}000
\end{align}
$$

・Multi-Head Attention
$N=80, d_{model}=16384, h=128, d_{k}=128, d_{v}=128$を元にパラメータ数は下記のように計算できます。
$$
\large
\begin{align}
2 N d_{model} h(d_{k}+d_{v}) &= 2 \times 80 \times 16384 \times 128 \times (128+128) \\
&= 85{,}899{,}345{,}920
\end{align}
$$

・FFN
$N=32, D=16384$の場合のパラメータ数は下記のように概算できます。
$$
\large
\begin{align}
8ND^2 &= 8 \times 80 \times 16384^{2} \\
&= 171{,}798{,}691{,}840
\end{align}
$$

よって、パラメータの総数は下記のように概算できます。
$$
\large
\begin{align}
& 524{,}288{,}000 + 85{,}899{,}345{,}920 + 171{,}798{,}691{,}840 \\
&= 258{,}222{,}325{,}760 = 2.58 \times 10^{11}
\end{align}
$$

上記は$258$Bなので、表の値と概ね一致することが確認できます。

GLaM

PaLM

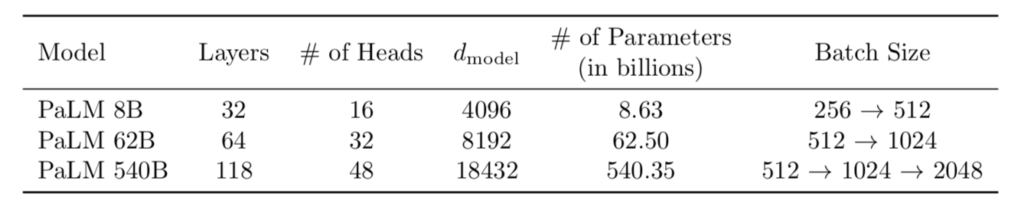
PaLM論文のパラメータ設定は上記より確認できます。基本的にはGPT$3$と同様にTransformer decoderの構成が用いられます。

$8$B

・Embedding
$V=256000, D=4096$を元にパラメータ数は下記のように計算できます。
$$
\large
\begin{align}
V \times D &= 256000 \times 4096 \\
&= 1{,}048{,}576{,}000
\end{align}
$$

$V=256000$はPaLMの論文を参照しました。

・Multi-Head Attention
$N=32, d_{model}=4096, h=16, d_{k}=256, d_{v}=256$を元にパラメータ数は下記のように計算できます。
$$
\large
\begin{align}
2 N d_{model} h(d_{k}+d_{v}) &= 2 \times 32 \times 4096 \times 16 \times (256+256) \\
&= 2{,}147{,}483{,}648
\end{align}
$$

・FFN
$N=32, D=4096$の場合のパラメータ数は下記のように概算できます。
$$
\large
\begin{align}
8ND^2 &= 8 \times 32 \times 4096^{2} \\
&= 4{,}294{,}967{,}296
\end{align}
$$

よって、パラメータの総数は下記のように概算できます。
$$
\large
\begin{align}
& 1{,}048{,}576{,}000 + 2{,}147{,}483{,}648 + 4{,}294{,}967{,}296 \\
&= 7{,}491{,}026{,}944 = 7.49 \times 10^{9}
\end{align}
$$

上記は$7.49$Bなので、表の値$8$Bと概ね一致することが確認できます。

$62$B

・Embedding
$V=256000, D=8192$を元にパラメータ数は下記のように計算できます。
$$
\large
\begin{align}
V \times D &= 256000 \times 8192 \\
&= 2{,}097{,}152{,}000
\end{align}
$$

・Multi-Head Attention
$N=64, d_{model}=8192, h=32, d_{k}=256, d_{v}=256$を元にパラメータ数は下記のように計算できます。
$$
\large
\begin{align}
2 N d_{model} h(d_{k}+d_{v}) &= 2 \times 32 \times 4096 \times 16 \times (256+256) \\
&= 17{,}179{,}869{,}184
\end{align}
$$

・FFN
$N=32, D=4096$の場合のパラメータ数は下記のように概算できます。
$$
\large
\begin{align}
8ND^2 &= 8 \times 64 \times 8192^{2} \\
&= 34{,}359{,}738{,}368
\end{align}
$$

よって、パラメータの総数は下記のように概算できます。
$$
\large
\begin{align}
& 2{,}097{,}152{,}000 + 17{,}179{,}869{,}184 + 34{,}359{,}738{,}368 \\
&= 53{,}636{,}759{,}552 = 5.36 \times 10^{10}
\end{align}
$$

上記は$53.6$Bなので、表の値$62$Bと概ね一致することが確認できます。

$540$B

・Embedding
$V=256000, D=18432$を元にパラメータ数は下記のように計算できます。
$$
\large
\begin{align}
V \times D &= 256000 \times 18432 \\
&= 4{,}718{,}592{,}000
\end{align}
$$

・Multi-Head Attention
$N=118, d_{model}=18432, h=72, d_{k}=256, d_{v}=256$を元にパラメータ数は下記のように計算できます。
$$
\large
\begin{align}
2 N d_{model} h(d_{k}+d_{v}) &= 2 \times 118 \times 18432 \times 72 \times (256+256) \\
&= 160{,}356{,}630{,}528
\end{align}
$$

・FFN
$N=118, D=18432$の場合のパラメータ数は下記のように概算できます。
$$
\large
\begin{align}
8ND^2 &= 8 \times 118 \times 18432^{2} \\
&= 320{,}713{,}261{,}056
\end{align}
$$

よって、パラメータの総数は下記のように概算できます。
$$
\large
\begin{align}
& 4{,}718{,}592{,}000 + 160{,}356{,}630{,}528 + 320{,}713{,}261{,}056 \\
&= 485{,}280{,}579{,}584 = 4.85 \times 10^{11}
\end{align}
$$

上記は$485$Bなので、表の値$540$Bと概ね一致することが確認できます。

参考

・Transformer論文：Attention is All you need$[2017]$
・BERT論文
・T$5$論文
・GPT$2$論文
・GPT$3$論文
・PaLM論文
・Transformer decoder論文
・直感的に理解するTransformer(運営者作成)