【LoRA】Low-Rank Adaptationの概要とTransformerへの導入

Fine-Tuningを行うにあたって、低ランクの行列分解に基づく手法であるLoRA(Low-Rank Adaptation)は実用上の観点から大変有力な手法です。当記事ではLoRAの概要とLoRAのTransformerへの適用について取りまとめました。
LoRAの論文である「LoRA: Low-Rank Aaptation of Large Language Models」の内容を参考に作成を行いました。

・用語/公式解説
https://www.hello-statisticians.com/explain-terms

Contents

1 LoRAの概要
2 TransformerへのLoRAの導入

LoRAの概要

パラメータ行列の分解

LoRA(Low-Rank Adaptation)ではFine-Tuningの際に全結合層(MLP)の計算に用いるパラメータ行列の分解を行います。たとえばパラメータ行列$W \in \mathbb{R}^{D \times D}$を用いる場合、$W$は下記のように分解することができます。
$$
\large
\begin{align}
W & \longrightarrow XY \\
X & \in \mathbb{R}^{D \times r}, \, Y \in \mathbb{R}^{r \times D}
\end{align}
$$

上記のように分解を行う場合、$D=10{,}000, r=10$であれば「$W$のパラメータ数」と「$X$と$Y$のパラメータ数の合計」はそれぞれ下記のように計算できます。
・$W$のパラメータ数
$$
\large
\begin{align}
10{,}000 \times 10{,}000 = 10^{8}
\end{align}
$$

・$X$と$Y$のパラメータ数の合計
$$
\large
\begin{align}
10,000 \times 10 + 10 \times 10{,}000 = 2 \times 10^{4}
\end{align}
$$

上記のようにLoRAではパラメータ$W$を$XY$のように分解してFine-Tuningの際に$X$と$Y$とそれぞれ学習を行います。このような処理を行うことでFine-Tuningの際の学習パラメータを減らすことが可能になります。

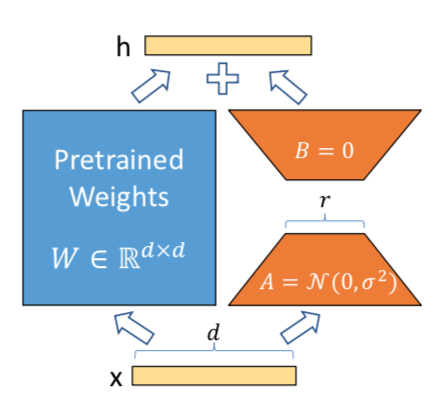
LoRAの処理の概要は上図からも確認できます。パラメータの初期値は$r \times D$の行列の値を正規分布$\mathcal{N}(0, \sigma^{2})$に基づいてサンプリングし、$D \times r$の行列を零行列で用意します¹。

図では$W \in \mathbb{R}^{D \times D}$が前提である一方で、論文の本文では$d \times k$で表記されている箇所があることは合わせて注意しておくと良いと思います。

一部のパラメータのみのFine-Tuning

Fine-Tuning時にLoRAを用いるにあたっては、基本的に全てのパラメータを用いずに一部のパラメータのみのFine-Tuningを行います。どのパラメータをFine-TuningするかはPre-trained modelやdownstream taskの特性に合わせて検討されます。

推論時の処理

LoRAではFine-Tuning時にパラメータ$W$をUpdateするのではなく、初期値が$0$の$\Delta W$に蓄積させるような処理が行われます。逆に推論時にはFine-Tuning時に学習した結果の$\Delta W$に対応する$W$に対して$W + \Delta W$を計算することで推論を行うことができます。

このような枠組みでFine-Tuningや推論を行うことで、推論時の処理を大きく変えないことが可能です。また、大元のパラメータの値を変えないことから、LoRAの入れ替えをスムーズに行うことが可能であり、アプリケーションへの反映がしやすくなります。

TransformerへのLoRAの導入

TransformerにおけるMLP

TransformerではMultiHead Attention時のlinear projectionと$2$層FFN(FeedForward Network)の$2$つの処理をMLPと見なすことができ、LoRA(Low-Rank Adaptation)を適用することが可能です²。

ネットワーク分析から直感的に理解するTransformerの仕組みと処理の流れ

LoRAの論文ではMultiHead Attention時の$W_q, W_k, W_v, W_o$を用いるlinear projectionのみ実験されておりFFNはfuture workの課題とされているので、以下$W_q, W_k, W_v, W_o$についてのみ確認を行います。

MultiHead AttentionのどのパラメータにLoRAを用いるか

LoRA論文のSection$\, 7.1$ではTransformerにおけるMultiHead AttentionのどのパラメータにLoRAを用いるかについて実験を元に考察が行われています。LoRA論文では$1{,}750$億のパラメータ数で構成されるGPT-$3$に対し、LoRAで用いるパラメータ数を$1{,}800$万とする条件下で実験が行われており、「$r=8$で$W_q, W_k, W_v, W_o$をどれか$1$つだけ用いるパターン」と「$r=4$かつ$2$つのパラメータを用いるパターン」、「$r=2$かつ$4$つ全てのパラメータを学習させるパターン」についてそれぞれパフォーマンスが計測されます。$1{,}800$万は$96 \times 12288 \times 8 \times 2 = 18{,}874{,}368$に基づきます。

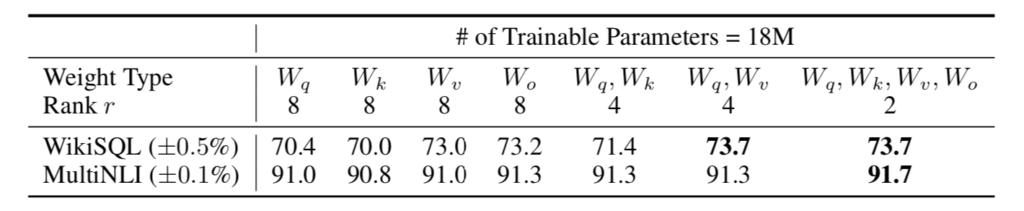
上記の表より、$r$を大きくするよりFine-Tuning対象のパラメータを増やすのが有力であるということが確認できます。この結果から、それほど複雑でないFine-Tuningタスクでは行列のランクが小さくても十分であると見なすことができます³。

また、$W_q, W_k, W_v$の学習にあたっては、一般的なMultiHead Attentionの処理はヘッド毎にパラメータ行列を計算するように立式される一方で、$D \times D$のパラメータ行列で計算した後に分割する演算で表すこともできます。このような点に基づいてMultiHead AttentionにおけるLoRAでは$D \times D$を$D \times r$と$r \times D$で分割し、学習を行うことが可能です。

LoRAではFine-Tuning時にパラメータ$W$をUpdateするのではなく初期値が$0$の$\Delta W$に蓄積させるような処理が行われるので、学習前の$\Delta W$が零行列となるように初期値を設定する必要があります。 ↩︎
MLPと見なせるかではなく、処理にパラメータ行列の積の演算が含まれるかで判断するのがシンプルで良いと思います。 ↩︎
LoRA論文では$r=2$でも十分であったのはタスクが簡単であったからと推察されており、たとえば多言語が前提となる場合は$r=2$では十分でない可能性があると記載されています。 ↩︎