Principal Anglesに基づくLoRAで用いる行列の最適なランク$r$の計算

LoRA(Low-Rank Adaptation)の論文ではPrincipal Angleに基づいてTransformerにおけるLoRAで用いる行列のランク$r$について実験が行われます。当記事ではPrincipal Angleの基本的な内容からLoRA論文の内容まで取りまとめを行いました。
LoRAの論文である「LoRA: Low-Rank Aaptation of Large Language Models」や「Matrix Computations」の内容を参考に作成を行いました。

・用語/公式解説
https://www.hello-statisticians.com/explain-terms

Principal Anglesの計算

行列のrangeとnullspace

$\mathbb{R}^{n} \longrightarrow \mathbb{R}^{m}$の線形写像に対応する行列$A \in \mathbb{R}^{m \times n}$について、$\mathbb{R}^{m}$の部分空間$\mathrm{ran}(A)$を下記のように定義する。
$$
\large
\begin{align}
\mathrm{ran}(A) = \{ y \in \mathbb{R}^{m} : \, y = Ax \quad \mathrm{for} \,\, \mathrm{some} \,\, x \in \mathbb{R}^{n} \}
\end{align}
$$

上記の部分空間を行列$A$のrangeといい、$\mathrm{ran}(A)$のように表す。

同様に$\mathbb{R}^{n}$の部分空間$\mathrm{null}(A)$を下記のように定義する。
$$
\large
\begin{align}
\mathrm{null}(A) = \{ x \in \mathbb{R}^{n} : \, Ax = 0 \}
\end{align}
$$

上記の部分空間を行列$A$のnullspaceといい、$\mathrm{null}(A)$のように表す¹。

また、下記が成立することも合わせて抑えておくと良い。
$$
\large
\begin{align}
\mathrm{dim}(\mathrm{ran}(A)) = n \, – \, \mathrm{dim}(\mathrm{null}(A))
\end{align}
$$

線形写像と部分空間

行列$A \in \mathbb{R}^{n \times p}$と行列$B \in \mathbb{R}^{n \times q}$を元に、部分空間$F$と$G$を下記のように定義する。
$$
\large
\begin{align}
F &= \mathrm{ran}(A) \\
G &= \mathrm{ran}(B)
\end{align}
$$

$p, q$については下記が成立すると仮定する。
$$
\large
\begin{align}
1 \leq q = \mathrm{dim}(F) \leq \mathrm{dim}(G) = p
\end{align}
$$

次項以降では、部分空間$F$と部分空間$G$の類似度を計算するにあたって、Principal AngleやPrincipal Vectorの定義を行う。

Principal Anglesの定義

部分空間$F$と部分空間$G$についてPrincipal Angles$\{ \theta_{i} \}_{i=1}^{q}$とPrincipal Vectors$\{ f_{i}, g_{i} \}_{i=1}^{q}$を下記の式が成立するように定義する。
$$
\large
\begin{align}
\cos{\theta_{k}} &= f_{k}^{\mathrm{T}} g_{k} = \max_{f \in F} \max_{g \in G} f^{\mathrm{T}} g \\
||f||_{2} &= 1, \quad ||g||_{2} = 1 \\
f^{\mathrm{T}}[f_1, \cdots , f_{k-1}] &= 0, \quad g^{\mathrm{T}}[g_1, \cdots , g_{k-1}] = 0
\end{align}
$$

上記の式に基づいて$i=1$から$i=q$まで、$\theta_{i}, \, f_{i}, \, g_{i}$をそれぞれ取得する。

また、$\cos{\theta}$は$\displaystyle 0 \leq \theta \leq \frac{\pi}{2}$で$\theta$について単調減少関数であることからPrincipal Angles$\{ \theta_{i} \}_{i=1}^{q}$について下記が成立する。
$$
\large
\begin{align}
0 \leq \theta_{1} \leq \cdots \leq \theta_{q} \leq \frac{\pi}{2} \quad (1)
\end{align}
$$

QR分解

行列$A \in \mathbb{R}^{n \times p}$、$B \in \mathbb{R}^{n \times q}$について下記のようなQR分解を仮定する。
$$
\large
\begin{align}
A &= Q_{A} R_{A}, \, Q_{A} \in \mathbb{R}^{n \times p}, \, R_{A} \in \mathbb{R}^{p \times p} \\
B &= Q_{B} R_{B}, \, Q_{B} \in \mathbb{R}^{n \times q}, \, R_{A} \in \mathbb{R}^{q \times q}
\end{align}
$$

QR分解については下記でも詳しく取り扱った。

グラム・シュミットの正規直交化に基づくQR分解とQR法を用いた固有値の近似計算の概要と実装

SVD

$Q_{A}^{\mathrm{T}} Q_{B} \in \mathbb{R}^{p \times q}$について下記のようなSVDを行う。
$$
\large
\begin{align}
Q_{A}^{\mathrm{T}} Q_{B} &= Y \Sigma Z^{\mathrm{T}} \quad (2) \\
Y \in \mathbb{R}^{p \times p}, \, & \Sigma \in \mathbb{R}^{p \times q}, \, Z \in \mathbb{R}^{p \times q}
\end{align}
$$

上記の行列$Y$と$Z$の$i$列目をそれぞれ$y_i \in \mathbb{R}^{p \times 1}, z_i \in \mathbb{R}^{q \times 1}$、$\Sigma$の$(i,i)$成分を$\sigma_{i}$とおくとき、$(2)$式は下記のように表すことができる。
$$
\large
\begin{align}
Q_{A}^{\mathrm{T}} Q_{B} &= Y \Sigma Z^{\mathrm{T}} = \sum_{i=1}^{q} \sigma_{i} y_{i} z_{i}^{\mathrm{T}} \quad (2)’ \\
y_i \in \mathbb{R}^{p \times 1}, \, & z_{i}^{\mathrm{T}} \in \mathbb{R}^{1 \times q}, \, y_{i} z_{i}^{\mathrm{T}} \in \mathbb{R}^{p \times q}
\end{align}
$$

ここで$||Q_{A}^{\mathrm{T}} Q_{B}||_{2} \leq 1$より、$0 \leq \sigma_{i} \leq 1$が成立するので、$\sigma_{i} = \cos{\theta_{i}}$とおく。ここで$Q_{A}Y, Q_{B}Z$を下記のように定義する。
$$
\large
\begin{align}
Q_{A}Y &= [f_1| \cdots | f_p] \in \mathbb{R}^{n \times p} \\
Q_{B}Z &= [g_1| \cdots | g_q] \in \mathbb{R}^{n \times q}
\end{align}
$$

このとき、$f = Q_{A} u, \, u \in \mathbb{R}^{p}$、$g = Q_{B} v, \, v \in \mathbb{R}^{q}$とおくと、$f^{\mathrm{T}} g$は下記のように式変形することができる。
$$
\large
\begin{align}
f^{\mathrm{T}} g &= (Q_{A} u)^{\mathrm{T}} (Q_{B} v) \\
&= u^{\mathrm{T}} Q_{A}^{\mathrm{T}} Q_{B} v \\
&= u^{\mathrm{T}} (Q_{A}^{\mathrm{T}} Q_{B}) v \\
&= u^{\mathrm{T}} (Y \Sigma Z^{\mathrm{T}}) v \\
&= ((u^{\mathrm{T}} Y)^{\mathrm{T}})^{\mathrm{T}} \Sigma (Z^{\mathrm{T}} v) \\
&= (Y^{\mathrm{T}} u)^{\mathrm{T}} \Sigma (Z^{\mathrm{T}} v) \\
&= \sum_{i=1}^{q} \sigma_{i} (y_{i}^{\mathrm{T}} u) (z_{i}^{\mathrm{T}} v)
\end{align}
$$

ここで$(1)$より$\sigma_{1} \geq \cdots \geq \sigma_{q}$であるので、$u=y_{1}, \, v=z_{1}$のとき$f^{\mathrm{T}} g$は最大値$\sigma_{1}=\cos{\theta_{1}}$を取る。このとき$f_1=Q_{A}y_{1}, g_1=Q_{B} z_{1}$によってPrincipal Vectorも計算できる。このような手順に基づいてPrincipal Angles$\{ \theta_{i} \}_{i=1}^{q}$とPrincipal Vectors$\{ f_{i}, g_{i} \}_{i=1}^{q}$を$i=1$から$i=q$にかけて得ることができる。

Principal Angles and Vectorsを得るアルゴリズム

前項までの内容をアルゴリズムに直すと下記が得られる。

$[1]$ 行列$A \in \mathbb{R}^{n \times p}$と行列$B \in \mathbb{R}^{n \times q}$のQR分解を行う。
$$
\large
\begin{align}
A &= Q_{A} R_{A}, \, Q_{A} \in \mathbb{R}^{n \times p}, \, R_{A} \in \mathbb{R}^{p \times p} \\
B &= Q_{B} R_{B}, \, Q_{B} \in \mathbb{R}^{n \times q}, \, R_{B} \in \mathbb{R}^{q \times q}
\end{align}
$$

$[2]$ $C = Q_{A}^{\mathrm{T}} Q_{B}$とおき、$C$の特異値分解(SVD)を行う。
$$
\large
\begin{align}
C &= Y \Sigma Z^{\mathrm{T}} \\
Y^{\mathrm{T}} C Z &= \Sigma = \mathrm{diag}(\sigma_{k}) = \mathrm{diag}(\cos{\theta_{k}})
\end{align}
$$

上記より、Principal Anglesの$\{ \theta_{k} \}_{k=1}^{\min(p,q)}$が得られる。

$[3]$ $Q_{A} Y, Q_{B} Z$に基づいて$\{ f_{k}, g_{k} \}_{k=1}^{\min(p,q)}$を得る。

TransformerにおけるLoRAで用いる行列の最適ランクの計算

全体方針

LoRAの論文ではFine-Tuning時にMLP(Multi Layer Perceptron)処理におけるパラメータ行列$W$の学習を、低ランクの行列の積を元に行う。

【LoRA】Low-Rank Adaptationの概要とTransformerへの導入

LoRA論文のSection$\, 7.2$では行列のランク$r$を決めるにあたって、実験に基づく考察が行われている。この際に前節で取り扱った「線形写像に対応する行列が生成する部分空間」のPrincipal Anglesを用いて類似度の計算が行われる。

以下、$r=8$と$r=64$の場合における写像$A_{r=8} \in \mathbb{R}^{8 \times D}, A_{r=64} \in \mathbb{R}^{64 \times D}$に基づく類似度の計算について確認を行う。

LoRA論文における写像の類似度の定義

$A_{r=8}^{\mathrm{T}} \in \mathbb{R}^{D \times 8}, A_{r=64}^{\mathrm{T}} \in \mathbb{R}^{D \times 64}$のQR分解を下記のように定義する²。
$$
\large
\begin{align}
A_{r=8}^{\mathrm{T}} &= Q_{r=8} R_{r=8} = U_{A_{r=8}}^{\mathrm{T}} R_{r=8} \\
A_{r=64}^{\mathrm{T}} &= Q_{r=64} R_{r=64} = U_{A_{r=64}}^{\mathrm{T}} R_{r=64} \\
U_{A_{r=8}} & \in \mathbb{R}^{D \times 8}, \, U_{A_{r=64}} \in \mathbb{R}^{D \times 64}
\end{align}
$$

このとき、LoRA論文では「$U_{A_{r=8}}$の$i$列目までの行列$U^{i}_{A_{r=8}} \in \mathbb{R}^{D \times i}$による部分空間と$U_{A_{r=64}}$の$j$列目までの行列$U^{j}_{A_{r=64}} \in \mathbb{R}^{D \times j}$による部分空間の類似度」を$\phi(A_{r=8}, A_{r=64}, i, j)$のようにおき、下記のような式で定義する。
$$
\large
\begin{align}
\phi(A_{r=8}, A_{r=64}, i, j) = \frac{|| (U^{i}_{A_{r=8}})^{\mathrm{T}} U^{j}_{A_{r=64}} ||_{F}^{2}}{\min{(i,j)}} \in [0, 1]
\end{align}
$$

写像の類似度のPrincipal Anglesに基づく理解

$(U^{i}_{A_{r=8}})^{\mathrm{T}} U^{j}_{A_{r=64}} \in \mathbb{R}^{i \times j}$に下記のようにSVDを行う。
$$
\large
\begin{align}
(U^{i}_{A_{r=8}})^{\mathrm{T}} U^{j}_{A_{r=64}} &= Y \Sigma Z^{\mathrm{T}} \\
Y \in \mathrm{R}^{i \times i}, \, & \Sigma \in \mathbb{R}^{i \times j}, \, Z \in \mathbb{R}^{j \times j}
\end{align}
$$

このとき、$\Sigma$の対角成分の$\sigma_{1}, \cdots , \sigma_{\min(i,j)}$を$\sigma_{k} = \cos{\theta_{k}}$のように対応させたのが前節で取り扱ったPrincipal Anglesである。

「Grassmann discriminant analysis: a unifying view on subspace-based learning.」ではこの$\theta_{k}$を元に下記のようにProjection metricの$d_{P}(U^{i}_{A_{r=8}}, U^{j}_{A_{r=64}})$が定義される。
$$
\large
\begin{align}
d_{P}(U^{i}_{A_{r=8}}, U^{j}_{A_{r=64}}) &= \left( \sum_{k=1}^{m} \sin^{2}{\theta_{k}} \right)^{\frac{1}{2}} = \left( m \, – \, \sum_{k=1}^{m} \cos^{2}{\theta_{k}} \right)^{\frac{1}{2}} \\
m &= \min{(i,j)}
\end{align}
$$

ここでLoRA論文における$\phi(A_{r=8}, A_{r=64}, i, j)$は下記のように式変形を行うことができる³。
$$
\large
\begin{align}
\phi(A_{r=8}, A_{r=64}, i, j) &= \frac{|| (U^{i}_{A_{r=8}})^{\mathrm{T}} U^{j}_{A_{r=64}} ||_{F}^{2}}{m} \\
&= \frac{\sum_{k=1}^{m} \sigma_{k}^{2}}{m} \\
&= \frac{\sum_{k=1}^{m} \cos^{2}{\theta_{k}}}{m} \\
&= \frac{\sum_{k=1}^{m} (1 – \sin^{2}{\theta_{k}})}{m} \\
&= \frac{m \, – \, \sum_{k=1}^{m} \sin^{2}{\theta_{k}}}{m} \\
&= 1 \, – \, \frac{d_{P}(U^{i}_{A_{r=8}}, U^{j}_{A_{r=64}})}{m} \\
m &= \min{(i,j)}
\end{align}
$$

LoRA論文の実験結果の解釈

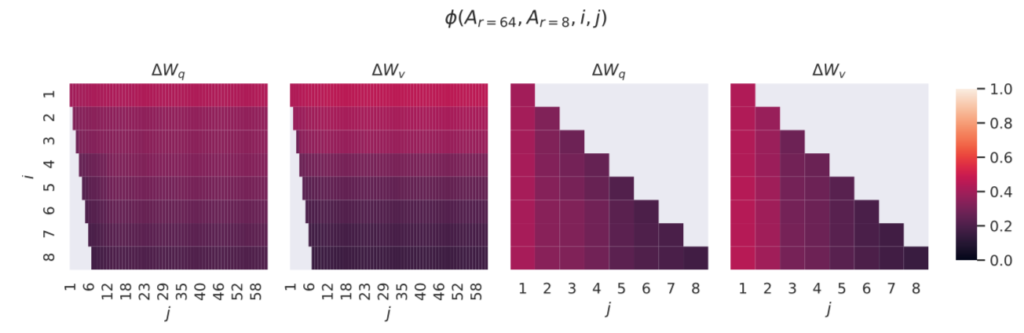
上図の結果より、$i$や$j$が小さいときベクトル空間が類似していることが確認できる。

参考

・LoRA論文

1. nullspaceの定義は線形代数における核(kernel)と同義だが、ここでは「Matrix Computations」の表記に基づいてnullspaceを用いた。 ↩︎
2. LoRA論文のSection$\, 7.2$では「SVDの右側のユニタリ行列を得る(we perform singular value decomposition and obtain the right-singular unitary matrices)」のように記載があるが、前節の内容に合わせてQR分解で統一させた。また、「右側を得る」という点については、$A^{\mathrm{T}} = QR$に対し、$A = ((A^{\mathrm{T}}))^{\mathrm{T}} = (QR)^{\mathrm{T}} = R^{\mathrm{T}} Q^{\mathrm{T}} = R^{\mathrm{T}}U$であるので、本文中のように$A^{\mathrm{T}}$のQR分解を行ったのちに$U = Q^{\mathrm{T}} \longrightarrow Q=U^{\mathrm{T}}$で表すのがわかりやすいと思われた。 ↩︎
3. LoRA論文では$\displaystyle \frac{1}{m}(1 \, – \, d_{P}(U^{i}_{A_{r=8}}, U^{j}_{A_{r=64}}))$のように結果が表されていたが、計算が合わなかったので結果のみ改変した。 ↩︎