グラム・シュミットの正規直交化に基づくQR分解とQR法を用いた固有値の近似計算の概要と実装

当記事ではQR分解(QR decomposition)に基づくQR法を用いた固有値の近似計算の概要とPythonを用いた実装に関して取り扱います。QR分解に関してはいくつか手法がありますが、当記事ではグラム・シュミットの正規直交化法に基づくQR分解の手順を主に確認しました。

・参考
Wikipedia QR分解
 Wikipedia QR法

Contents

1 手順の確認
- 1.1 グラム・シュミットの正規直交化法に基づくQR分解
- 1.2 QR分解とQR法
2 Pythonを用いた計算例

手順の確認

グラム・シュミットの正規直交化法に基づくQR分解

正射影の式から理解するグラム・シュミット(Gram–Schmidt)の正規直交化法

上記で取り扱ったグラム・シュミットの正規直交化法では、線型独立な$\vec{a}_{1}, \cdots, \vec{a}_{n}$に対して下記のように正規直交基底の$\vec{e}_{1}, \cdots, \vec{e}_{n}$の計算を行なった。
$$
\large
\begin{align}
\vec{u}_{1} &= \vec{a}_{1}, & \vec{e}_{1} = \frac{\vec{u}_{1}}{|\vec{u}_{1}|} \\
\vec{u}_{2} &= \vec{a}_{2} – \frac{\vec{a}_{1} \cdot \vec{a}_{2}}{|\vec{a}_{1}|^2} \vec{a}_{1}, & \vec{e}_{2} = \frac{\vec{u}_{2}}{|\vec{u}_{2}|} \\
\vec{u}_{3} &= \vec{a}_{3} – \frac{\vec{a}_{1} \cdot \vec{a}_{3}}{|\vec{a}_{1}|^2} \vec{a}_{1} – \frac{\vec{a}_{2} \cdot \vec{a}_{3}}{|\vec{a}_{2}|^2} \vec{a}_{2}, & \vec{e}_{3} = \frac{\vec{u}_{3}}{|\vec{u}_{3}|} \\
\vdots \\
\vec{u}_{n} &= \vec{a}_{n} – \sum_{k=1}^{n-1} \frac{\vec{a}_{k} \cdot \vec{a}_{n}}{|\vec{a}_{k}|^2} \vec{a}_{k}, & \vec{e}_{n} = \frac{\vec{u}_{n}}{|\vec{u}_{n}|}
\end{align}
$$

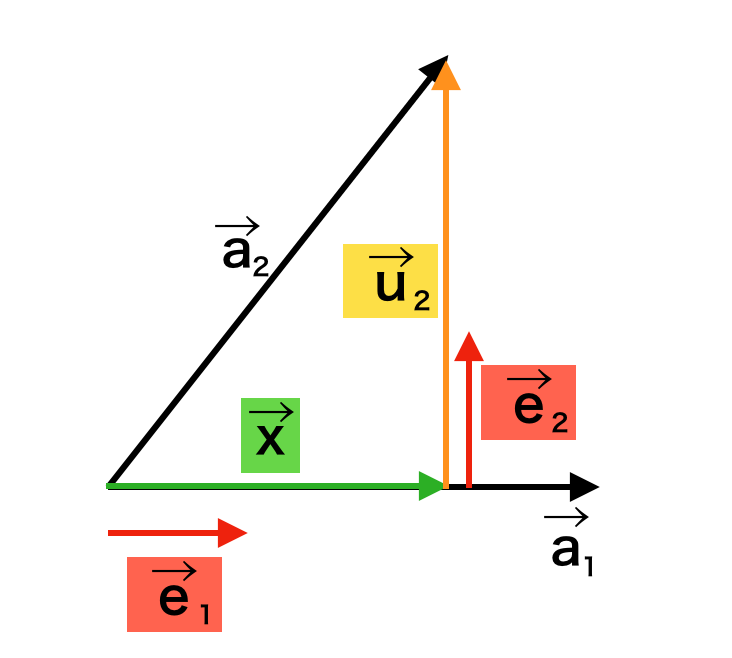
ここで上図に基づいて考えることで$\vec{a}_{k} \cdot \vec{e}_{k} = |\vec{u}_{k}|$が成立することを元にベクトル$\vec{a}_{k}$を$\vec{e}_{1}, \cdots, \vec{e}_{n}$を用いて下記のように表すことを考えることができる。
$$
\large
\begin{align}
\vec{a}_{1} &= (\vec{a}_{1} \cdot \vec{e}_{1}) \vec{e}_{1} \\
\vec{a}_{2} &= (\vec{e}_{1} \cdot \vec{a}_{2}) \vec{e}_{1} + (\vec{a}_{2} \cdot \vec{e}_{2}) \vec{e}_{2} \\
\vec{a}_{3} &= (\vec{e}_{1} \cdot \vec{a}_{3}) \vec{e}_{1} + (\vec{e}_{2} \cdot \vec{a}_{3}) \vec{e}_{2} + (\vec{a}_{3} \cdot \vec{e}_{3}) \vec{e}_{3} \\
\vdots \\
\vec{a}_{n} &= \sum_{k=1}^{n} (\vec{e}_{k} \cdot \vec{a}_{n}) \vec{e}_{k}
\end{align}
$$

上記は下記のような行列計算にまとめることができる。
$$
\large
\begin{align}
\left(\begin{array}{ccc} \vec{a}_{1} & \cdots & \vec{a}_{n} \end{array} \right) &= \left(\begin{array}{ccc} (\vec{a}_{1} \cdot \vec{e}_{1}) \vec{e}_{1} & \cdots & \displaystyle \sum_{k=1}^{n} (\vec{e}_{k} \cdot \vec{a}_{n}) \vec{e}_{k} \end{array} \right) \\
&= \left(\begin{array}{ccc} \vec{e}_{1} & \cdots & \vec{e}_{n} \end{array} \right) \left(\begin{array}{ccc} (\vec{a}_{1} \cdot \vec{e}_{1}) & (\vec{e}_{1} \cdot \vec{a}_{2}) & (\vec{e}_{1} \cdot \vec{a}_{3}) \\ 0 & (\vec{a}_{2} \cdot \vec{e}_{2}) & (\vec{e}_{2} \cdot \vec{a}_{3}) \\ 0 & 0 & (\vec{a}_{3} \cdot \vec{e}_{3}) \end{array} \right) \\
A &= QR
\end{align}
$$

上記の$Q$は直交行列、$R$は上三角行列であることがここまでの議論により確認できる。

QR分解とQR法

QR分解では$A=QR$のように行列$A$を直交行列$Q$と上三角行列$R$に分解を行う。ここで$A=QR$より、$R=Q^{-1}A=Q^{\mathrm{T}}A$である。ここで下記のように繰り返し手順を定める。
$$
\large
\begin{align}
A_{1} &= A \\
R_{k}Q_{k} &= A_{k} \\
A_{k+1} &= R_{k}Q_{k} = Q^{\mathrm{T}}_{k}A_{k}Q_{k}
\end{align}
$$

上記の計算を行うことで$A_{n}$の対角成分より下の要素が$0$に収束し、計算によって固有値が変わらないことから$A_{n}$の対角成分が固有値に一致する。この手法をQR法という。

Pythonを用いた計算例

QR分解の実装

グラム・シュミットの正規直交化に基づくQR分解は下記を実行することで行うことができる。計算例はデバッグもかねて「QR分解 Wikipedia」と同様な例を用いた。

import numpy as np

def QR_gram(X):
    U, Q, R = np.zeros([X.shape[0],X.shape[0]]), np.zeros([X.shape[0],X.shape[0]]), np.zeros([X.shape[0],X.shape[1]])
    U[:,0] = X[:,0]
    Q[:,0] = U[:,0]/np.linalg.norm(U[:,0])
    R[0,0] = np.dot(X[:,0],U[:,0]/np.linalg.norm(U[:,0]))
    for i in range(1,X.shape[0]):
       U[:,i] = X[:,i]
       for j in range(i):
           U[:,i] += -(np.dot(X[:,i],U[:,j])/np.dot(U[:,j],U[:,j]))*U[:,j]
           R[j,i] = np.dot(X[:,i],U[:,j]/np.linalg.norm(U[:,j]))
       Q[:,i] = U[:,i]/np.linalg.norm(U[:,i])
       R[i,i] = np.dot(X[:,i],U[:,i]/np.linalg.norm(U[:,i]))
    return Q, R

A = np.array([[12., -51., 4.], [6., 167., -68.], [-4., 24., -41]])
Q, R = QR_gram(A)

print("・Q:")
print(Q)
print("・R:")
print(R)
print("・re-calculated A=QR:")
print(np.dot(Q,R))
print("error: {}".format(np.linalg.norm(A-np.dot(Q,R))))

・実行結果

・Q
[[ 0.85714286 -0.39428571 -0.33142857]
 [ 0.42857143  0.90285714  0.03428571]
 [-0.28571429  0.17142857 -0.94285714]]
・R
[[  14.   21.  -14.]
 [   0.  175.  -70.]
 [   0.    0.   35.]]
・re-calculated A=QR:
[[  12.  -51.    4.]
 [   6.  167.  -68.]
 [  -4.   24.  -41.]]
 error: 1.76298382482e-14

$2 \times 2$正方行列における固有値の計算

下記を実行することで$2 \times 2$正方行列$\displaystyle A = \left(\begin{array}{cc} 2 & 1 \\ 1 & 2 \end{array} \right)$に対して固有値の計算を行うことができる。

A = np.array([[2., 1.], [1., 2.]])
Q, R = QR_gram(A)

A_k = A
Q_k, Q_k_inv = Q, Q.T
for i in range(5):
    Q_k, _ = QR_gram(A_k)
    Q_k_inv = Q_k.T
    A_k = np.dot(Q_k_inv,np.dot(A_k,Q_k))
    print("・STEP: {:.0f}".format(i+1))
    print(A_k)