グラム・シュミットの正規直交化法(Gram–Schmidt orthonormalization)は線型独立な有限個のベクトルで構成される部分空間と同様の部分空間を持つ正規直交系を作り出す手法です。当記事では正射影の式を元にグラム・シュミットの正規直交化法の仕組みに関して取りまとめました。
Contents
前提の理解
正射影の公式とその導出
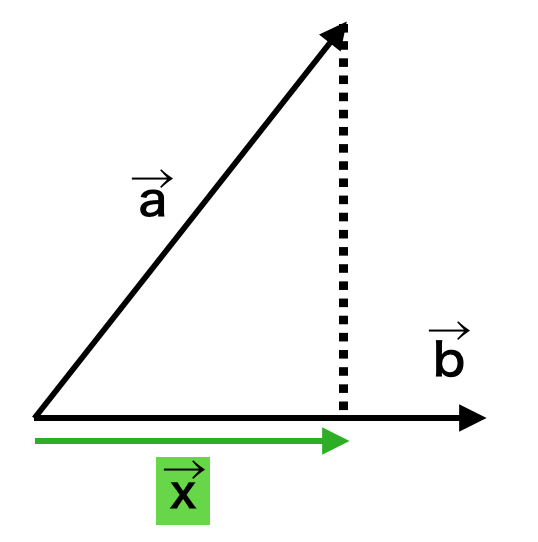
上記のように$\vec{a}, \vec{b}$を考える。このとき$\vec{a}$の$\vec{b}$への正射影を$\vec{x}$と定めると、$\vec{x}$は下記のように表すことができる。
$$
\large
\begin{align}
\vec{x} = \frac{\vec{a} \cdot \vec{b}}{|\vec{b}|^2} \vec{b} \quad (1)
\end{align}
$$
以下、$(1)$式のように$\vec{x}$が示せることの確認を行う。
導出にあたっては、ベクトル$\vec{x}$を$\vec{b}$と平行な単位ベクトルの定数倍であることに基づいて考える。ここで$\vec{b}$と平行な単位ベクトルを$\vec{e}$とおき、$\vec{x}=k\vec{e}$と定めると、$\vec{e}$と$k$は下記のように表せる。
$$
\large
\begin{align}
\vec{e} &= \frac{\vec{b}}{|\vec{b}|} \quad (2) \\
k &= |\vec{a}|\cos{\theta} \quad (3) \\
&= \frac{|\vec{a}||\vec{b}|\cos{\theta}}{|\vec{b}|} = \frac{\vec{a} \cdot \vec{b}}{|\vec{b}|}
\end{align}
$$
ここで$\vec{x}=k\vec{e}$に$(2)$式、$(3)$式を代入することで、下記のように$(1)$式を導出することができる。
$$
\large
\begin{align}
\vec{x} &= k \vec{e} \\
&= \frac{\vec{a} \cdot \vec{b}}{|\vec{b}|} \frac{\vec{b}}{|\vec{b}|} \\
&= \frac{\vec{a} \cdot \vec{b}}{|\vec{b}|^2} \vec{b}
\end{align}
$$
線型独立と部分空間
グラム・シュミットの正規直交化法
$2$次元平面におけるグラム・シュミットの正規直交化法
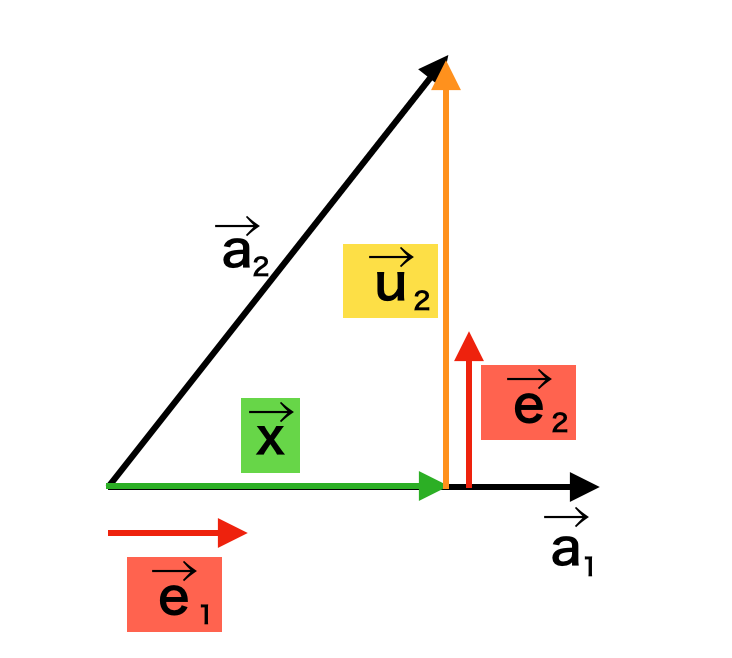
グラム・シュミットの正規直交化法は、上図のように線型独立である$\vec{a}_{1}, \vec{a}_{2}$が与えられた際に正規直交基底の$\vec{e}_{1}, \vec{e}_{2}$を得る手法である。
1) $\vec{a}_{1}$に平行な単位ベクトルを$\vec{e}_{1}$とおく。
2) $\vec{e}_{1}$に垂直なベクトル$\vec{u}_{2}$を$\vec{u}_{2}=\vec{a}_{2}-\vec{x}$を計算することで得る。ここで$\vec{x}$は$\vec{a}_{2}$から$\vec{a}_{1}$への正射影であるので、前節の「正射影の公式」を用いることで計算できる。
3) $\vec{u}_{2}$と平行な単位ベクトルを$\vec{e}_{2}$とおく。
上記に基づいて、$\vec{e}_{1}, \vec{e}_{2}$はそれぞれ下記のように計算できる。
$$
\large
\begin{align}
\vec{e}_{1} &= \frac{\vec{a}_{1}}{|\vec{a}_{1}|} \\
\vec{e}_{2} &= \frac{\vec{u}_{2}}{|\vec{u}_{2}|} \\
\vec{u}_{2} &= \vec{a}_{2} \, – \, \vec{x} = \vec{a}_{2} \, – \, \frac{\vec{a}_{1} \cdot \vec{a}_{2}}{|\vec{a}_{1}|^2} \vec{a}_{1}
\end{align}
$$
$n$次元空間におけるグラム・シュミットの正規直交化法
$n$次元空間におけるグラム・シュミットの正規直交化法は$2$次元平面と同様に考えることができるが、$\vec{e}_{3}$以降は累積を考慮する必要があることに注意しなければならない。具体的には$\vec{e}_{1}, \vec{e}_{2}, \cdots \vec{e}_{n}$は下記のように計算できる。
$$
\large
\begin{align}
\vec{u}_{1} &= \vec{a}_{1}, & \vec{e}_{1} = \frac{\vec{u}_{1}}{|\vec{u}_{1}|} \\
\vec{u}_{2} &= \vec{a}_{2} \, – \, \frac{\vec{a}_{1} \cdot \vec{a}_{2}}{|\vec{a}_{1}|^2} \vec{a}_{1}, & \vec{e}_{2} = \frac{\vec{u}_{2}}{|\vec{u}_{2}|} \\
\vec{u}_{3} &= \vec{a}_{3} \, – \, \frac{\vec{a}_{1} \cdot \vec{a}_{3}}{|\vec{a}_{1}|^2} \vec{a}_{1} \, – \, \frac{\vec{a}_{2} \cdot \vec{a}_{3}}{|\vec{a}_{2}|^2} \vec{a}_{2}, & \vec{e}_{3} = \frac{\vec{u}_{3}}{|\vec{u}_{3}|} \\
\vdots \\
\vec{u}_{n} &= \vec{a}_{n} \, – \, \sum_{k=1}^{n-1} \frac{\vec{a}_{k} \cdot \vec{a}_{n}}{|\vec{a}_{k}|^2} \vec{a}_{k}, & \vec{e}_{n} = \frac{\vec{u}_{n}}{|\vec{u}_{n}|}
\end{align}
$$

[…] 正射影の式から理解するグラム・シュミット(Gram–Schmidt)の正規直交化法 […]
[…] 正射影の式から理解するグラム・シュミット(Gram–Schmidt)の正規直交化法 […]
[…] 正射影の式から理解するグラム・シュミット(Gram–Schmidt)の正規直交化法 […]