計量ベクトル空間におけるノルム(norm)が$1$かつ直交する基底(basis)を正規直交基底(orthonormal basis)といいます。当記事では正規直交基底(orthonormal basis)の定義とグラム・シュミットの直交化に基づく作成手順について、取りまとめの作成を行いました。
作成にあたっては「チャート式シリーズ 大学教養 線形代数」の$7.1$節「内積と計量ベクトル空間」を主に参考にしました。
・数学まとめ
https://www.hello-statisticians.com/math_basic
Contents
正規直交基底
正規直交基底の定義
計量ベクトル空間$V$の基底を$\{ \mathbf{v}_{1}, \, \cdots , \, \mathbf{v}_{n} \}$と定義する。このとき下記が成立すれば$\{ \mathbf{v}_{1}, \, \cdots , \, \mathbf{v}_{n} \}$は正規直交基底である。
$[1] \,$ 「$\mathbf{v}_{1}, \, \cdots , \, \mathbf{v}_{n}$の任意の$2$つのベクトルが直交する」 $\iff$ 「$i = j$のとき$(\mathbf{v}_{i}, \mathbf{v}_{j}) = 1$、$i \neq j$のとき$(\mathbf{v}_{i}, \mathbf{v}_{j}) = 0$が成立する」
$[2] \,$ 「全ての基底ベクトルのノルムが$1$である」 $\iff$ 「任意のベクトル$\mathbf{v}_{i}$について$||\mathbf{v}_{i}||=1$が成立する」
グラム・シュミットの直交化と正規直交基底の作成手順
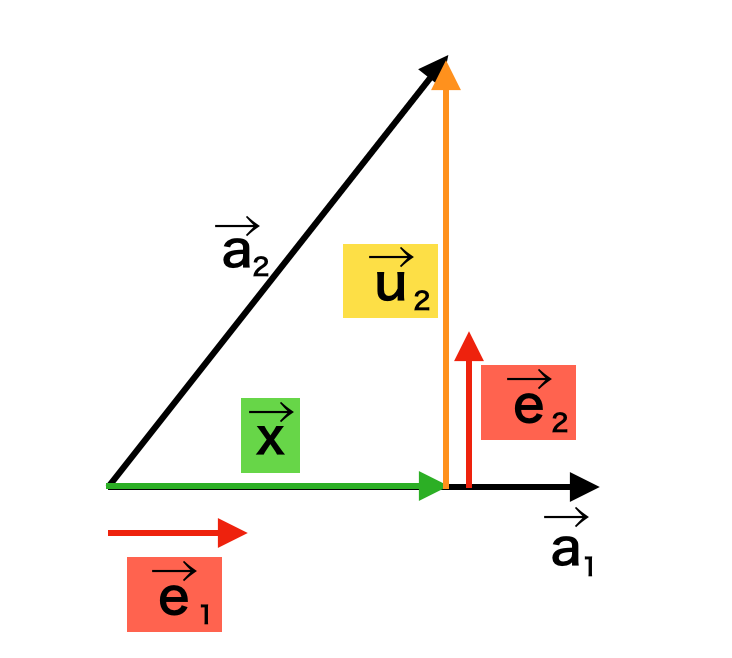
グラム・シュミットの直交化/正規直交化は上図を元に理解すると良い。詳しい手順は下記で取りまとめた。
正規直交基底の具体例
以下、「チャート式シリーズ 大学教養 線形代数」の例題の確認を行う。
基本例題$137$
$$
\large
\begin{align}
\left\{ \left( \begin{array}{c} 1 \\ -1 \\ 0 \end{array} \right), \, \left( \begin{array}{c} 3 \\ 3 \\ 2 \end{array} \right), \, \left( \begin{array}{c} -1 \\ -1 \\ 3 \end{array} \right) \right\} \quad (1)
\end{align}
$$
$(1)$を左から$\mathbf{v}_{1}, \mathbf{v}_{2}, \mathbf{v}_{3}$とおく。このときベクトルの標準内積はそれぞれ下記のように計算できる。
$$
\large
\begin{align}
(\mathbf{v}_{1}, \mathbf{v}_{2}) &= 3 \, – \, 3 = 0 \\
(\mathbf{v}_{2}, \mathbf{v}_{3}) &= -3 \, – \, 3 + 6 = 0 \\
(\mathbf{v}_{3}, \mathbf{v}_{1}) &= -1 + 1 = 0
\end{align}
$$
上記より$\mathbf{v}_{1}, \mathbf{v}_{2}, \mathbf{v}_{3}$はそれぞれ直交しており、$1$次独立である。よって$(1)$はベクトル空間$\mathbb{R}^{3}$の基底であり、正規直交基底は$(1)$を正規化することで下記のように得られる。
$$
\large
\begin{align}
\left\{ \frac{1}{\sqrt{2}}\left( \begin{array}{c} 1 \\ -1 \\ 0 \end{array} \right), \, \frac{1}{\sqrt{22}}\left( \begin{array}{c} 3 \\ 3 \\ 2 \end{array} \right), \, \frac{1}{\sqrt{11}}\left( \begin{array}{c} -1 \\ -1 \\ 3 \end{array} \right) \right\}
\end{align}
$$
基本例題$138$
・$[1]$
$$
\large
\begin{align}
\left\{ \mathbf{v}_{1}=\left( \begin{array}{c} 1 \\ 2 \end{array} \right), \, \mathbf{v}_{2}=\left( \begin{array}{c} 1 \\ 1 \end{array} \right) \right\}
\end{align}
$$
$\mathbf{v}_{1}’=\mathbf{v}_{1}$とおく。このとき、$\mathbf{v}_{1}’$に垂直なベクトルを$\mathbf{v}_{2}’$とおくと下記が成立する。
$$
\large
\begin{align}
\mathbf{v}_{2}’ &= \mathbf{v}_{2} \, – \, x_{1} \mathbf{v}_{1}’ \\
(\mathbf{v}_{1}’, \mathbf{v}_{2}’) &= 0
\end{align}
$$
上記は下記のように$x_1$について解くことができる。
$$
\large
\begin{align}
(\mathbf{v}_{1}’, \mathbf{v}_{2}’) &= 0 \\
(\mathbf{v}_{1}’, \mathbf{v}_{2} \, – \, x_{1} \mathbf{v}_{1}’) &= 0 \\
(\mathbf{v}_{1}’, \mathbf{v}_{2}) \, – \, x_{1} (\mathbf{v}_{1}’, \mathbf{v}_{1}’) &= 0 \\
x_{1} (1^{2} + 2^{2}) &= 1 + 2 \\
x_{1} &= \frac{3}{5}
\end{align}
$$
よって$\mathbf{v}_{2}’$は下記のように得られる。
$$
\large
\begin{align}
\mathbf{v}_{2}’ &= \mathbf{v}_{2} \, – \, x_{1} \mathbf{v}_{1}’ \\
&= \left( \begin{array}{c} 1 \\ 1 \end{array} \right) \, – \, \frac{3}{5} \left( \begin{array}{c} 1 \\ 2 \end{array} \right) \\
&= \frac{1}{5} \left( \begin{array}{c} 2 \\ -1 \end{array} \right)
\end{align}
$$
よって、下記のような正規直交基底${ \mathbf{e}_{1}, \mathbf{e}_{2} }$が得られる。
$$
\large
\begin{align}
\left\{ \mathbf{e}_{1} = \frac{1}{\sqrt{5}}\left( \begin{array}{c} 1 \\ 2 \end{array} \right), \, \mathbf{e}_{2} = \frac{1}{\sqrt{5}}\left( \begin{array}{c} 2 \\ -1 \end{array} \right) \right\}
\end{align}
$$
