勾配に基づく最適化はよく行われる一方で、楕円に対して勾配法を適用する際に収束がなかなか進まない場合があります。このような場合に役立つ手法が共役勾配法(Conjugate Gradient Method)です。当記事では共役勾配法の原理や具体例について取りまとめました。
https://ja.wikipedia.org/wiki/共役勾配法
Contents
前提の確認
問題設定
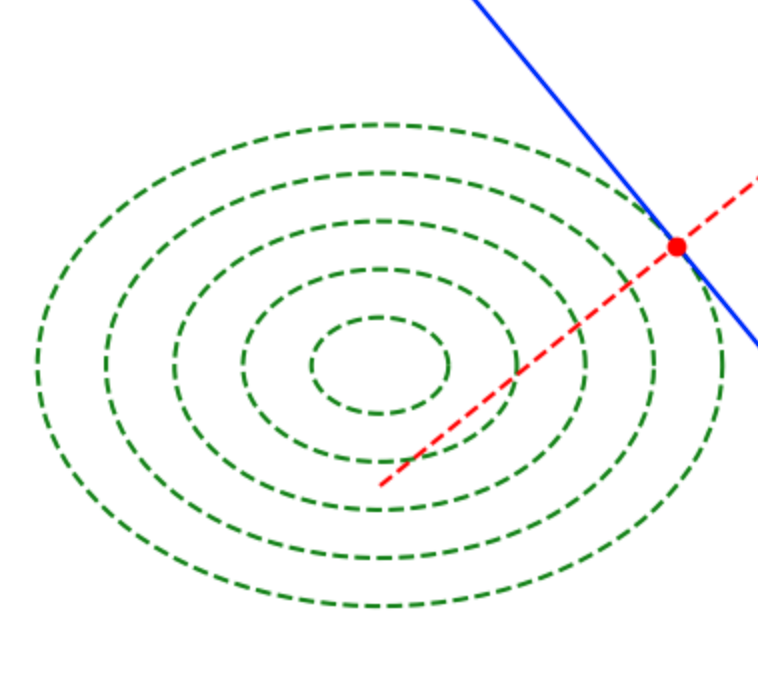
オーソドックスな勾配降下(Gradient Descent)法は最適化にあたって有効である場合が多いが、上記のように同心楕円の等高線を持つ関数を取り扱う場合、初期値によっては楕円の等高線の法線ベクトルや勾配が楕円の中心を向かないことで収束がなかなか進まない。
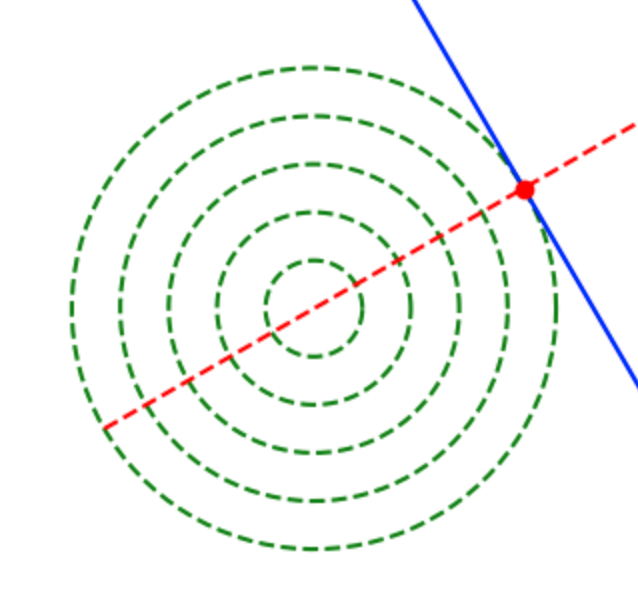
一方で上記のような同心円の等高線を持つ関数を取り扱う場合は同心円の等高線の法線ベクトルや勾配が円の中心を向くので、最適解をスムーズに得ることができる。
次節では同心楕円における最適化を行うにあたって、共役勾配法(Conjugate Gradient Method)のアルゴリズムの確認を行う。
二次形式を用いた立式
$$
\large
\begin{align}
f(\mathbf{x}) &= \frac{1}{2} \mathbf{x}^{\mathrm{T}} A \mathbf{x} – \mathbf{b}^{\mathrm{T}} \mathbf{x} + c \quad (1.1) \\
\mathbf{x} & \in \mathbb{R}^{2}, \, A \in \mathbb{R}^{2 \times 2}, \, A^{\mathrm{T}}=A, \, \mathbf{b} \in \mathbb{R}^{2}, \, c \in \mathbb{R}
\end{align}
$$
上記のような二次形式$f(\mathbf{x})$の最小化問題を定義する。当項では簡易化にあたって$\mathbf{x}$は$2$次元のベクトルを定義したが、$3$次元以上も同様に取り扱うことができる。
$(1.1)$式は下記のように平方完成を行うことができる。
$$
\large
\begin{align}
f(\mathbf{x}) &= \frac{1}{2} \mathbf{x}^{\mathrm{T}} A \mathbf{x} – \mathbf{b}^{\mathrm{T}} \mathbf{x} + c \quad (1.1) \\
&= \frac{1}{2} \left( \mathbf{x}^{\mathrm{T}} A \mathbf{x} – 2 \mathbf{b}^{\mathrm{T}} \right) + c \\
&= \frac{1}{2} \left( \mathbf{x} – A^{-1} \mathbf{b} \right)^{\mathrm{T}} A \left( \mathbf{x} – A^{-1} \mathbf{b} \right) + c’ \quad (1.2)
\end{align}
$$
上記より、$f(\mathbf{x})$は$A^{-1} b$を中心とする同心楕円を描くことが確認できる。よって基本的には$\mathbf{x}^{\mathrm{T}} A \mathbf{x}$の最適化を取り扱えれば$(1.1)$式も単に平行移動で取り扱うことができる。
二次形式の平方完成については下記で詳しく取り扱った。
二次形式の式と楕円
前項の「二次形式を用いた立式」では$f(\mathbf{x})$と定義したが、関数の等高線の形状を取り扱うにあたっては関数の平行移動である$g(\mathbf{x}) = \mathbf{x}^{\mathrm{T}} A \mathbf{x}$のみを確認すれば十分である。よって以下では$g(\mathbf{x})$の等高線を確認する。
$2$次対称行列$A$の固有値を$\lambda_1, \lambda_2(\lambda_1 \neq \lambda_2)$、長さ$1$に正規化された固有ベクトルを$\mathbf{e}_{1}, \mathbf{e}_{2}$と定義するとき、任意のベクトル$\mathbf{x}$は係数$a_1, a_2$を用いて下記のように表せる。
$$
\large
\begin{align}
\mathbf{x} = a_1 \mathbf{e}_{1} + a_2 \mathbf{e}_{2}
\end{align}
$$
このとき、$g(\mathbf{x})$は下記のように表せる。
$$
\large
\begin{align}
g(\mathbf{x}) &= (a_1 \mathbf{e}_{1} + a_2 \mathbf{e}_{2})^{\mathrm{T}} A (a_1 \mathbf{e}_{1} + a_2 \mathbf{e}_{2}) \\
&= (a_1 \mathbf{e}_{1} + a_2 \mathbf{e}_{2})^{\mathrm{T}} (\lambda_1 a_1 \mathbf{e}_{1} + \lambda_2 a_2 \mathbf{e}_{2}) \\
&= \lambda_{1} a_1^{2} + \lambda_{2} a_2^{2} \quad (1.3)
\end{align}
$$
上記の計算にあたっては対称行列$A$の固有ベクトルが直交することを用いた。詳しい導出は下記で取り扱った。
ここで等高線$g(\mathbf{x})=C$の方程式は下記のように変形できる。
$$
\large
\begin{align}
g(\mathbf{x}) &= \lambda_{1} a_1^{2} + \lambda_{2} a_2^{2} = C \quad (1.4) \\
\frac{a_1^2}{\sqrt{C/\lambda_{1}}^{2}} + \frac{a_2^2}{\sqrt{C/\lambda_{2}}^{2}} &= 1 \quad (1.5)
\end{align}
$$
上記は$a_1, a_2$に関する楕円の方程式を表すが、ここで$\mathbf{x} = a_1 \mathbf{e}_{1} + a_2 \mathbf{e}_{2}$であることより、$\displaystyle \frac{\sqrt{\mathbf{e}_{1}}}{\lambda_{1}}$と$\displaystyle \frac{\sqrt{\mathbf{e}_{2}}}{\lambda_{2}}$を基底に持つ楕円が式に対応することが確認できる。
対称行列Aに関する直交・共役
$$
\large
\begin{align}
\mathbf{u}^{\mathrm{T}} A \mathbf{v} &= 0 \quad (1.6) \\
\mathbf{u} \in \mathbb{R}^{2}, \, & \mathbf{v} \in \mathbb{R}^{2}, \, A \in \mathbb{R}^{2 \times 2}
\end{align}
$$
上記が成立するとき、ベクトル$\mathbf{u}, \, \mathbf{v}$は対称行列$A$に対して「共役である」または「直交する」という。ここで対称行列$A$が$A = P^{\mathrm{T}} P$のように分解できるとき、$(1.6)$式は下記のように変形できる。
$$
\large
\begin{align}
\mathbf{u}^{\mathrm{T}} A \mathbf{v} &= 0 \quad (1.6) \\
\mathbf{u}^{\mathrm{T}} P^{\mathrm{T}} P \mathbf{v} &= 0 \\
(P \mathbf{u})^{\mathrm{T}} (P \mathbf{v}) &= 0
\end{align}
$$
上記の$P$を用いて$\hat{\mathbf{x}} = P \mathbf{x}$のような変換を行うと、$\hat{\mathbf{x}}$の空間では同心楕円の等高線が同心円の等高線に変換される。ここで$(P \mathbf{u})^{\mathrm{T}} (P \mathbf{v}) = 0$は、二次形式の等高線が同心円で表される空間で$(P \mathbf{u})^{\mathrm{T}} \perp (P \mathbf{v})$が成立することを表す。よって、$\mathbf{x}$の空間では等高線の接点からのベクトルが同心楕円の中心の方向に一致する。
共役勾配法は上記に基づいて、「等高線が同心楕円で表される関数の最適化における収束の効率化」を行う手法である。
グラム・シュミットの正規直交化
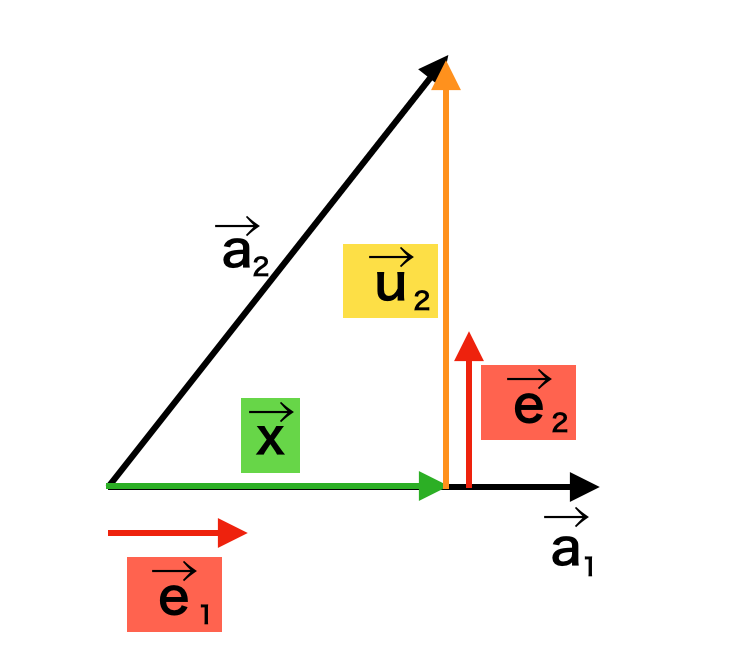
グラム・シュミットの正規直交化法は、上図のように線型独立である$\vec{a}_{1}, \vec{a}_{2}$が与えられた際に正規直交基底の$\vec{e}_{1}, \vec{e}_{2}$を得る手法である。以下、簡単に手順の確認を行う。
1) $\vec{a}_{1}$に平行な単位ベクトルを$\vec{e}_{1}$とおく。
2) $\vec{e}_{1}$に垂直なベクトル$\vec{u}_{2}$を$\vec{u}_{2}=\vec{a}_{2}-\vec{x}$を計算することで得る。ここで$\vec{x}$は$\vec{a}_{2}$から$\vec{a}_{1}$への正射影を計算することで得られる。
3) $\vec{u}_{2}$と平行な単位ベクトルを$\vec{e}_{2}$とおく。
上記に基づいて、$\vec{e}_{1}, \vec{e}_{2}$はそれぞれ下記のように計算できる。
$$
\large
\begin{align}
\vec{e}_{1} &= \frac{\vec{a}_{1}}{|\vec{a}_{1}|} \\
\vec{u}_{2} &= \vec{a}_{2} – \vec{x} = \vec{a}_{2} – \frac{\vec{a}_{1} \cdot \vec{a}_{2}}{|\vec{a}_{1}|^2} \vec{a}_{1} \\
\vec{e}_{2} &= \frac{\vec{u}_{2}}{|\vec{u}_{2}|}
\end{align}
$$
グラム・シュミットの正規直交化について詳しくは下記で取り扱った。
共役勾配法
共役勾配法の原理
「共役勾配法」は「グラム・シュミットの正規直交化」における「直交」を「対称行列$A$に関する共役・直交」に基づいて取り扱った手法である。以下、線型独立である$\mathbf{v}_{1}, \mathbf{v}_{2}$を元に対称行列$A$に互いに共役であるベクトル$\mathbf{d}_1, \mathbf{d}_2$をグラム・シュミットの直交化に基づいて生成を行う。$\displaystyle \mathbf{d}_1 = \mathbf{v}_{1}$とおくと、$\mathbf{d}_{2}$は下記のように得られる。
$$
\large
\begin{align}
\mathbf{d}_{2} = \mathbf{v}_{2} – \frac{\mathbf{v}_{1}^{\mathrm{T}} A \mathbf{v}_{2}}{\mathbf{v}_{1}^{\mathrm{T}} A \mathbf{v}_{1}} \mathbf{v}_{1} \quad (2.1)
\end{align}
$$
上記の式は正規化を行わなかったので、前節の式とやや異なることに注意が必要である。$\mathbf{d}_1$の楕円の等高線との接点から$\mathbf{d}_{2}$の方向にline searchなどを用いることで関数の最小点である楕円の中心を得ることができる。また、最小点$\mathbf{x}^{*}$について下記が成立する。
$$
\large
\begin{align}
\nabla f(\mathbf{x}) &= A \mathbf{x} – \mathbf{b} \quad (1.1)’ \\
A \mathbf{x}^{*} – \mathbf{b} &= \mathbf{0} \\
A \mathbf{x}^{*} &= \mathbf{b} \quad (2.2)
\end{align}
$$
$(2.2)$式より、ここで得られた最小点$\mathbf{x}^{*}$は$A \mathbf{x} = \mathbf{b}$の解に一致することも確認できる。
また、$(2.1)$式を一般化することで、線型独立である$\mathbf{v}_{1}, \cdots , \mathbf{v}_{p}$を元に対称行列$A$に互いに共役であるベクトル$\mathbf{d}_{j}, \, (i=2, \cdots, p)$を下記のように得ることができる。
$$
\large
\begin{align}
\mathbf{d}_{j} = \mathbf{v}_{j} – \sum_{i=1}^{j-1} \frac{\mathbf{v}_{i}^{\mathrm{T}} A \mathbf{v}_{j}}{\mathbf{v}_{i}^{\mathrm{T}} A \mathbf{v}_{i}} \mathbf{v}_{i}
\end{align}
$$
共役勾配法の計算例
$$
\large
\begin{align}
f(\mathbf{x}) &= \frac{1}{2} \mathbf{x}^{\mathrm{T}} A \mathbf{x} – \mathbf{b}^{\mathrm{T}} \mathbf{x} + c \quad (2.3) \\
A &= 2 \left(\begin{array}{cc} 2 & 1 \\ 1 & 2 \end{array} \right) \\
\mathbf{b} &= \left(\begin{array}{c} 0 \\ 0 \end{array} \right), \, c=0
\end{align}
$$
以下、上記のように定義した二次形式$f(\mathbf{x})$の最適化を共役勾配法を用いて行う。$f(\mathbf{x})$は下記のように表すことができる。
$$
\large
\begin{align}
f(\mathbf{x}) &= \left(\begin{array}{cc} x_1 & x_2 \end{array} \right) \left(\begin{array}{cc} 2 & 1 \\ 1 & 2 \end{array} \right) \left(\begin{array}{c} x_1 \\ x_2 \end{array} \right) \quad (2.3)’ \\
A’ &= \left(\begin{array}{cc} 2 & 1 \\ 1 & 2 \end{array} \right)
\end{align}
$$
ここで行列$A’$の固有値は$\lambda_1=3, \lambda_2=1$、$\lambda_1=3, \lambda_2=1$、固有ベクトルは$\displaystyle \mathbf{u}_{1} = \left(\begin{array}{c} 1 \\ 1 \end{array} \right), \, \mathbf{u}_{2} = \left(\begin{array}{c} -1 \\ 1 \end{array} \right)$が得られる。導出過程はオーソドックスな固有値・固有ベクトルの計算なので省略するが、この固有値と固有ベクトルがそれぞれ適切であることは下記の等式が成立することからそれぞれ確認できる。
$$
\large
\begin{align}
\left(\begin{array}{cc} 2 & 1 \\ 1 & 2 \end{array} \right) \left(\begin{array}{c} 1 \\ 1 \end{array} \right) &= 3 \left(\begin{array}{c} 1 \\ 1 \end{array} \right) \\
\left(\begin{array}{cc} 2 & 1 \\ 1 & 2 \end{array} \right) \left(\begin{array}{c} -1 \\ 1 \end{array} \right) &= \left(\begin{array}{c} -1 \\ 1 \end{array} \right)
\end{align}
$$
上記に基づいて、二次形式$f(\mathbf{x})$の等高線は下図のように表される。
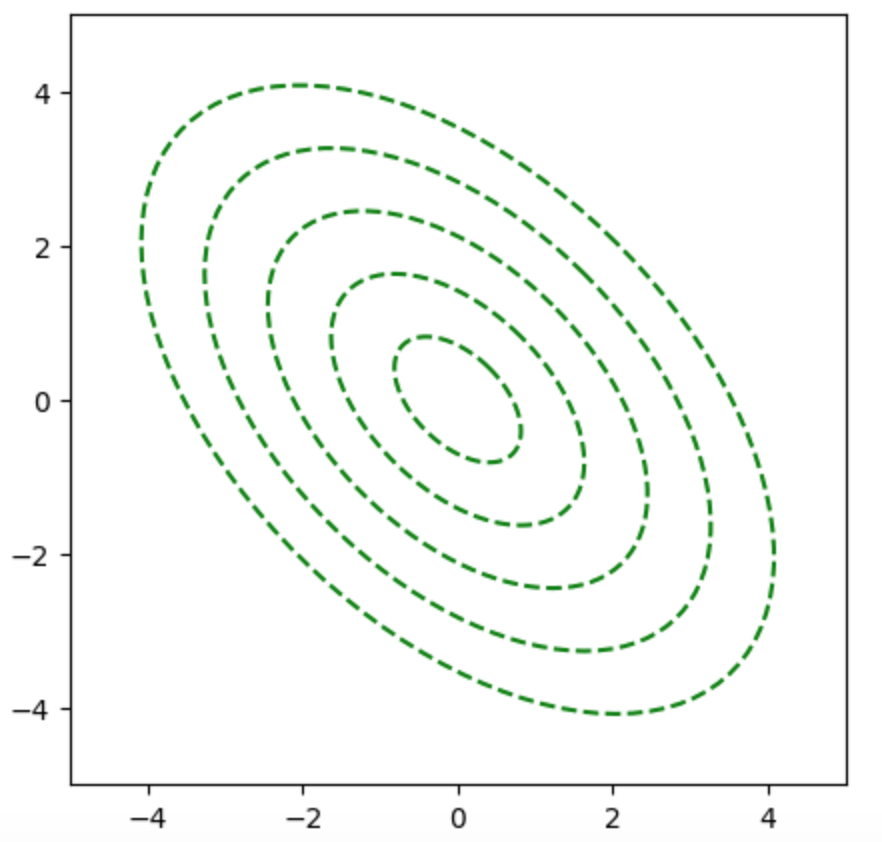
ここで楕円上の点における勾配は楕円の法線ベクトルに一致するが、勾配ベクトルは下図のように楕円の中心を向かない。
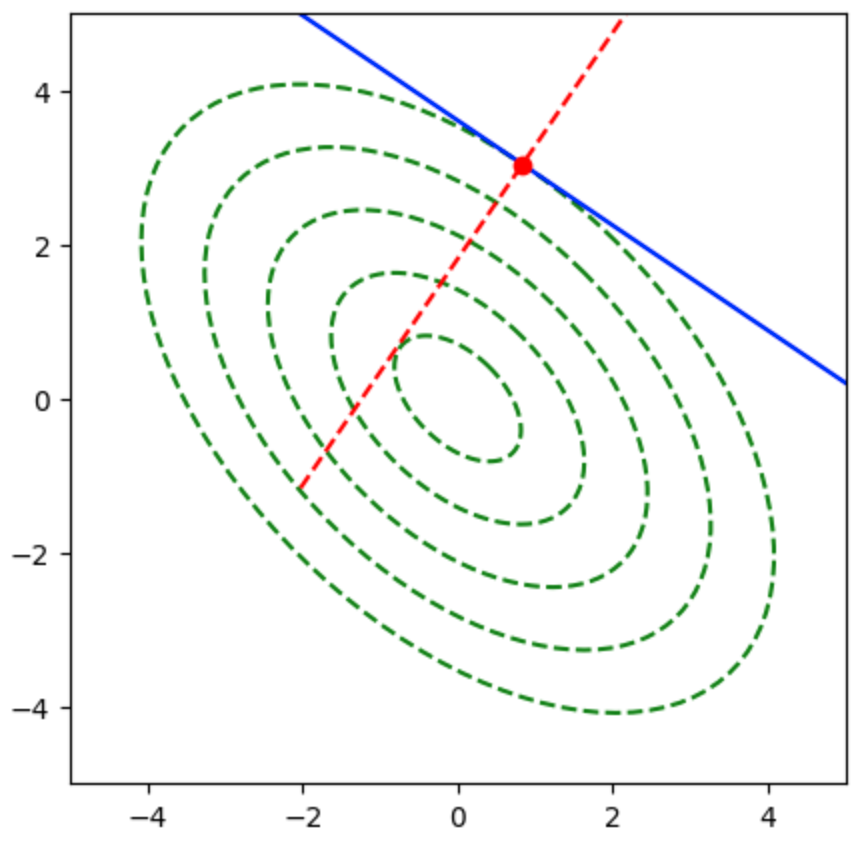
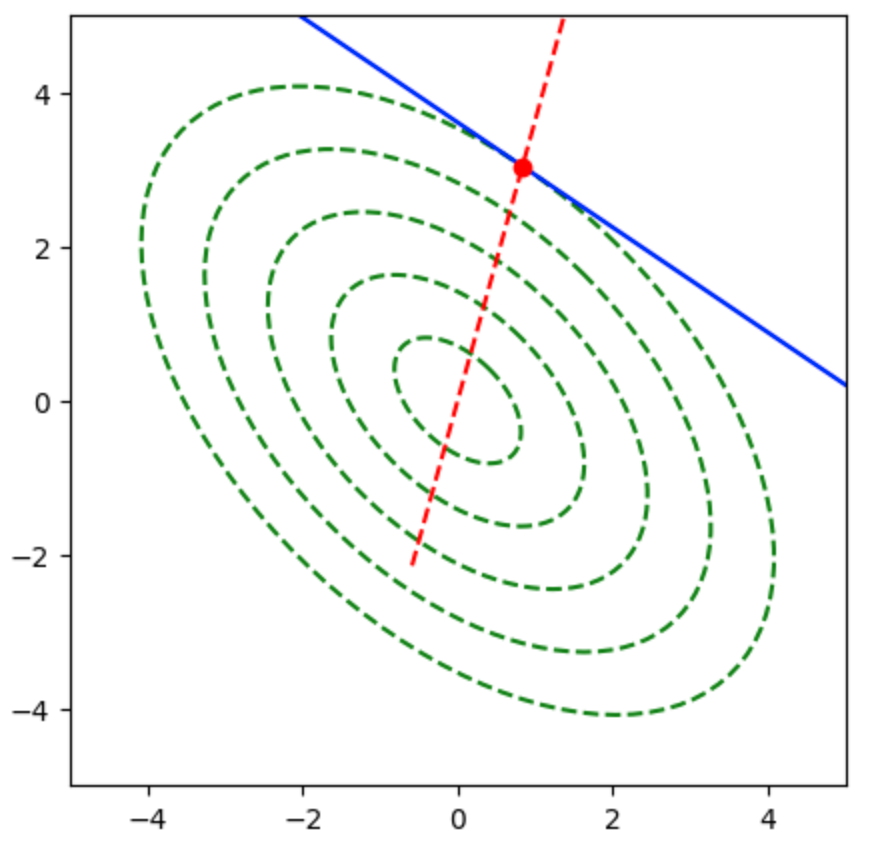
上図では勾配ベクトルが楕円の中心を向かないので、$A’$について共役な方向を計算する必要がある。前項の共役勾配法を用いることで下記のような結果を得ることができる。
共役勾配法のプログラムについては下記で詳しく取り扱った。

[…] 共役勾配法(Conjugate Gradient Method)の原理と具体的な計算例 […]
[…] $(1)$式の詳細は「共役勾配法の原理と具体的な計算例」、「共役勾配法のPythonを用いた計算例」などで取り扱った。ここで$(1)$式の対称行列$A$は数値で与えられることもあるが、多変数関数の最適化などの場合はヘッセ行列$H$が用いられる。 […]
[…] 共役勾配法(Conjugate Gradient Method)の原理と具体的な計算例 […]