行列分解まとめ①では特異値分解(SVD; singular value decomposition)などの基本的な行列分解の手法に関してまとめました。②では近年用いられているFactorization MachinesやDeepFMに関してご紹介します。
Contents
Factorization Machines
Factorization Machinesの問題設定
特異値分解(SVD; singular value decomposition)などの行列分解の手法では行列$X$に対して$X = UV^{\mathrm{T}}$のような分解を行うことのみを考えたが、Factorization Machinesでは回帰のように$(X,y)$に対して主に取り扱いが行われる。Factorization Machinesの論文のFigure.$1$では下記のように$(X,y)$の具体例が紹介される。

ここで上記の例では「青枠のUserがオレンジの枠のMovieを$y$のように評価した」ということに基づいて$X$と$y$の具体例が作成されている。このとき、特定のUserに対する特定のMovieの評価がないときに、評価を予測するというのがここでの問題設定である。
上記の$X$は行列の要素の多くが$0$を持つスパース(sparse)な行列になるが、このようなスパースな行列の取り扱いにあたってFactorization Machinesが考案された。
・参考
Factorization Machines論文 Section.$2$ Prediction Under Sparsity
Factorization Machinesの予測式
Factorization Machinesの予測式は下記のように定義される。
$$
\large
\begin{align}
\hat{y}(x) &= w_{0} + \sum_{i=1}^{n} w_i x_i + \sum_{i=1}^{n} \sum_{j=i+1}^{n} \langle v_i, v_j \rangle x_i x_j \quad (1) \\
w_{0} &\in \mathbb{R}, w \in \mathbb{R}^{n}, V \in \mathbb{R}^{n \times k} \quad (2) \\
\langle v_i, v_j \rangle &= \sum_{f=1}^{k} v_{i,f} \cdot v_{j,f} \quad (3)
\end{align}
$$
上記はFactorization Machines論文の$(1)$〜$(3)$式に対応する。ここで$n$は$X$の行数や$y$の個数に対応し、$k$は$V$で表される潜在空間の次元に対応すると考えることができる。式だけだと少々分かりにくいので概略を下記のように図式化を行った。
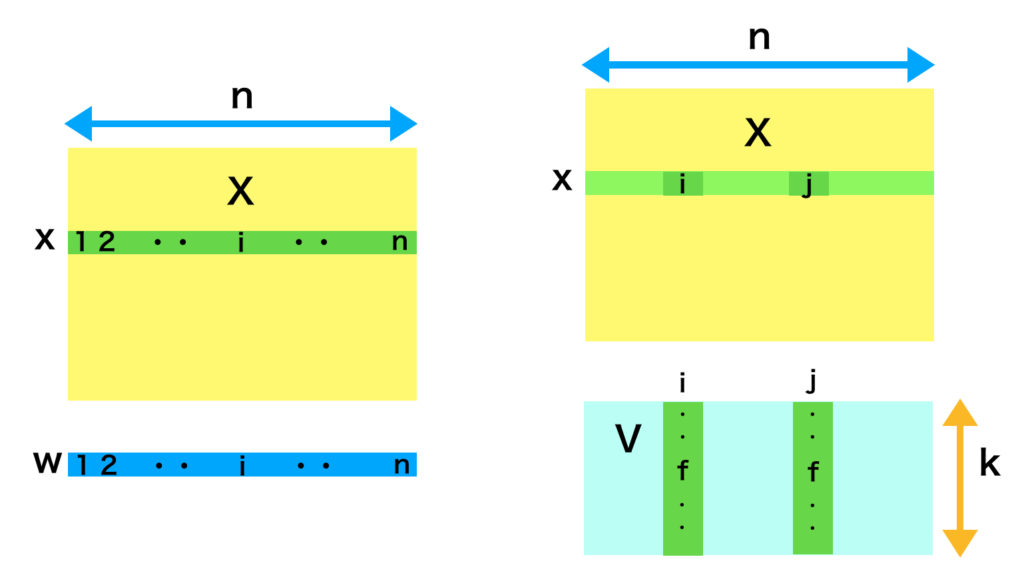
・参考
Factorization Machines論文 Section.$3$-A Factorization Machine Model
Factorization Machinesのパラメータ推定
Factorization Machinesのパラメータ推定では前項の$(2)$式で表した、$w_{0} \in \mathbb{R}, w \in \mathbb{R}^{n}, V \in \mathbb{R}^{n \times k} $の推定を行う。
ここでパラメータの推定にあたっては確率的勾配降下法(SGD)を用いる。$(1)$式のそれぞれのパラメータでの偏微分はそれぞれ下記のように表される。
$$
\large
\begin{align}
\frac{\partial}{\partial w_0} \hat{y}(x) &= 1 \\
\frac{\partial}{\partial w_i} \hat{y}(x) &= x_i \\
\frac{\partial}{\partial v_{i,f}} \hat{y}(x) &= x_i \sum_{j=1}^{n} v_{j,f} x_{j} – v_{i,f} x_{i}^2
\end{align}
$$
ここで上記の$\hat{y}(x)$はloss functionそのものではないが、論文の数式をそのまま用いた。一方で、loss functionが予測と実測の差を数値化したものである以上、合成関数の微分的に上記の式が出てくることは理解しておくと良い。たとえば二乗和誤差の場合は$((y-\hat{y}(x))^2)’ = 2(y-\hat{y}(x))\hat{y}(x)’$のような計算になるので、$\hat{y}(x)$の偏微分がわかっていればスムーズに各勾配の要素の計算を行うことができる。
また、$\displaystyle \frac{\partial}{\partial v_{i,f}} \hat{y}(x)$の式がやや複雑であるが、$\displaystyle \hat{y}(x) = w_{0} + \sum_{i=1}^{n} w_i x_i + \sum_{i=1}^{n} \sum_{j=i+1}^{n} \langle v_i, v_j \rangle x_i x_j$の式に出てくる$\displaystyle \sum_{i=1}^{n} \sum_{j=i+1}^{n}$より、$i < j$であり、これは上三角行列のように対角成分と左下の要素が$0$である行列を考え、これに基づいて式を解釈するとわかりやすいと思われる。
・参考
Factorization Machines論文 Section.$3$-C Learning Factorization Machines
DeepFM
DeepFMの概要
DeepFMはFactorization-Machineに基づくニューラルネットワークであり、FM ComponentとDeep Componentの二つの要素から構成される。このことはDeepFM論文の$(1)$式で表されるので下記に表した。
$$
\large
\begin{align}
\hat{y} &= sigmoid(y_{FM} + y_{DNN}) \\
sigmoid(x) &= \frac{1}{1+\exp(-x)}, \quad \hat{y} \in (0,1)
\end{align}
$$
また、パラメータ学習にあたってはAdamなどが用いられる。以下、FM ComponentとDeep Componentの詳細に関してそれぞれ確認を行う。
FM Component
FM Componentは前節で取り扱ったFactorization Machinesの考え方に基づく。”Besides a linear (order-1) interactions among features, FM models pairwise (order-2) feature interactions as inner product of respective feature latent vectors”と表現されるように、特徴量の$1$次式に加えて、$2$つの特徴量の相互作用を潜在ベクトルの内積に基づいて計算すると考えると良い。Factorization Machinesで定義される$V$は潜在空間(latent space)を取り扱っており、これは通常の行列分解を潜在空間と考えることと同様に理解することができる。
DeepFM論文の$(2)$式ではFM Componentが下記のように表記される。
$$
\large
\begin{align}
y_{FM} &= \langle w, x \rangle + \sum_{i=1}^{d} \sum_{j=i+1}^{d} \langle V_i, V_j \rangle x_i \cdot x_j
\end{align}
$$
上記はFactorization Machinesの式を行列表記を用いて整理を行った式であると考えることができる。これを図式化を行ったのが論文のFigure.$2$である。
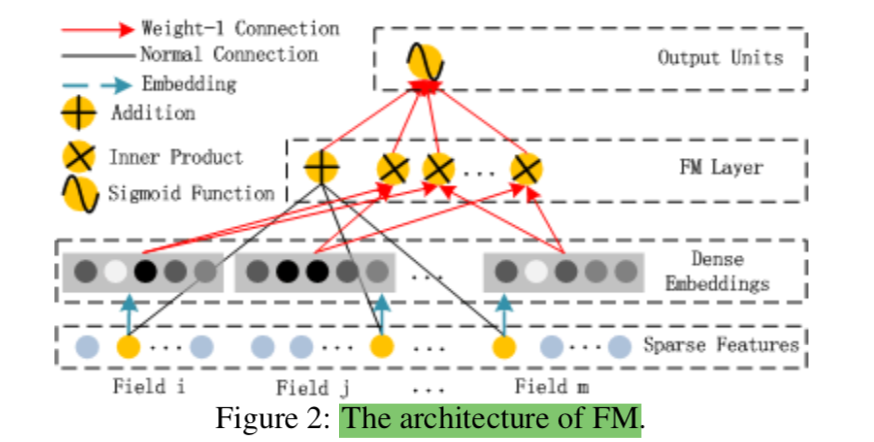
論文のFigure.$2$の解釈にあたっては、Dense Embeddingsが$V_i, V_j$に対応すると考えればよい。また、FM layerではAdditionとInner Productの二つの演算が表されていることにも着目すると良い。
Deep Component
Deep Componentの概要は論文のFigure.$3$で図示される。
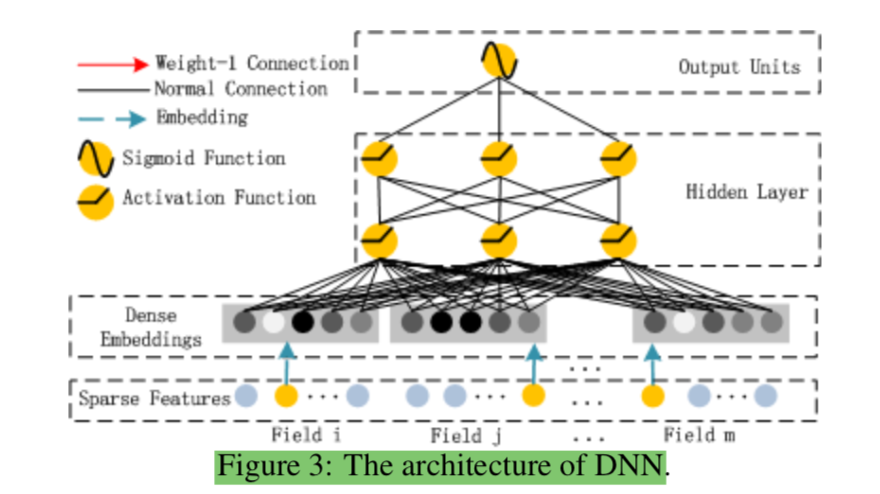
DeepFM論文 Figure 3: The architecture of DNN
上記のHidden Layerより上に関しては基本的には通常のMulti Layer Perceptronと同様であるが、ここで着目する必要があるのがDense Embeddingを作成する処理である。Dense Embeddingの作成は論文のFigure.$4$で表される。
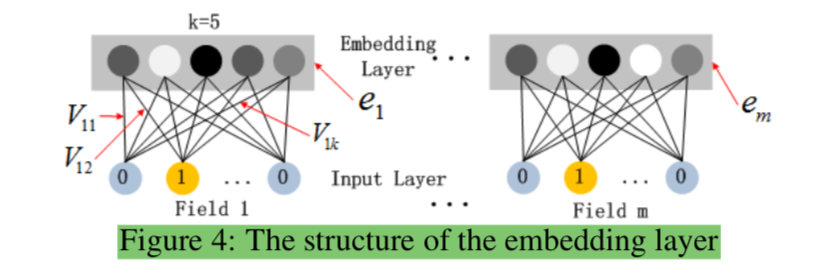
上記で表されるembedding layerの構造の理解にあたっては、「①$0$以外の値を持つ特徴量(Field)を固定長$k$のembeddingに変換する」、「②Input LayerからEmbeding Layerの計算にあたっては潜在パラメータの$V$を用いる」をそれぞれ抑えておくとよい。
・参考
DeepFM論文 Section.$2$.$1$ DeepFM
