確率分布の類似度を計算するにあたってKLダイバージェンスが用いられることが多いですが、式の解釈に関してわかりやすくまとめられていることが少ないように思われます。そこで当記事ではKLダイバージェンスの概略が把握できるように正規分布間のKLダイバージェンスの値を具体的にグラフ化を行いました。
「パターン認識と機械学習」の$1.6$節の「Information Theory」などを主に参考に作成を行いました。
・用語/公式解説
https://www.hello-statisticians.com/explain-terms
Contents
前提の確認
KLダイバージェンスの式定義
$$
\large
\begin{align}
KL(p||q) &= – \int p(x) \ln{q(x)} dx – \left[ – \int p(x) \ln{p(x)} dx \right] \\
&= – \int p(x) \ln{\frac{q(x)}{p(x)}} dx \quad (1.113)
\end{align}
$$
確率分布$p(x)$に関するKLダイバージェンスは「パターン認識と機械学習」の$(1.113)$式のように定義されるので、上記に表した。$p(x)$の$x$は多次元ベクトルを考える場合もあるが、当記事では以下$1$次元の$x$のみを取り扱う。
正規分布間のKLダイバージェンス
$2$つの正規分布$p(x)=\mathcal{N}(x|\mu,\sigma^{2}), q(x)=\mathcal{N}(x|m,s^{2})$間のKLダイバージェンス$KL(p||q)$は「パターン認識と機械学習」の演習$1.30$より、下記のように表すことができる。
$$
\large
\begin{align}
KL(p||q) &= – \int p(x) \ln{\frac{q(x)}{p(x)}} dx \quad (1.113) \\
&= \ln{\frac{s}{\sigma}} + \frac{1}{2} \left[ \frac{1}{s^2}(\mu^2+\sigma^2 – 2 \mu m + m^2) – 1 \right] \\
&= \frac{1}{2} \left[ \ln{\frac{s^2}{\sigma^2}} + \frac{\sigma^2-s^2}{s^2} + \frac{(\mu-m)^2}{s^2} \right] \quad (1)
\end{align}
$$
上記の結果を元に、$\mu,\sigma^{2},m,s^2$の値を変化させたときにKLダイバージェンスの$KL(p||q)$がどのように変化するかに関して、以下確認を行う。
KLダイバージェンスの値の変化とグラフ
$2$つの正規分布が一致する場合
$p(x)=q(x)$が成立する場合、$\mu=m,\sigma^{2}=s^2$であり、$(1)$式に代入すると下記のように変形できる。
$$
\large
\begin{align}
KL(p||q) &= \frac{1}{2} \left[ \ln{\frac{s^2}{\sigma^2}} + \frac{\sigma^2-s^2}{s^2} + \frac{(\mu-m)^2}{s^2} \right] \quad (1) \\
&= \frac{1}{2} \left[ \ln{\frac{s^2}{s^2}} + \frac{s^2-s^2}{s^2} + \frac{(m-m)^2}{s^2} \right] \\
&= 0
\end{align}
$$
上記は$p(x)=q(x)$のときに$KL(p||q)=0$であることに対応する。
分散が同一で平均を動かす場合
当項では$\sigma^{2}=s^2$が成立するときに$KL(p||q)$が$\mu=m$の値に基づいてどのように変化するかに関して確認を行う。
$$
\large
\begin{align}
KL(p||q) &= \frac{1}{2} \left[ \ln{\frac{s^2}{\sigma^2}} + \frac{\sigma^2-s^2}{s^2} + \frac{(\mu-m)^2}{s^2} \right] \quad (1) \\
&= \frac{1}{2} \left[ \ln{\frac{s^2}{s^2}} + \frac{s^2-s^2}{s^2} + \frac{(\mu-m)^2}{s^2} \right] \\
&= \frac{1}{2} \frac{(\mu-m)^2}{s^2}
\end{align}
$$
上記のようにKLダイバージェンスは$\mu-m$の$2$次関数で表される。ここで$\mu-m$を考えるにあたっては、二つのそれぞれの値ではなく「差」が重要であるので、グラフ化にあたっては$\Delta = \mu-m$のようにおき、$\Delta$を変数と見る。
$\Delta$を変数と見たときのKLダイバージェンスのグラフ化は下記を実行することで行える。なお、$2$つの正規分布の分散は$1^2,2^2,3^2$の$3$つを同時に表した。
import numpy as np
import matplotlib.pyplot as plt
delta = np.arange(-3.,3.01,0.01)
sigma2 = np.array([1.**2, 2.**2, 3.**2])
KL_color = ["green","blue","red"]
for i in range(sigma2.shape[0]):
KL = delta**2/sigma2[i]
plt.plot(delta,KL,color=KL_color[i],label="sigma^2: {:.0f}".format(sigma2[i]))
plt.legend()
plt.show()・実行結果
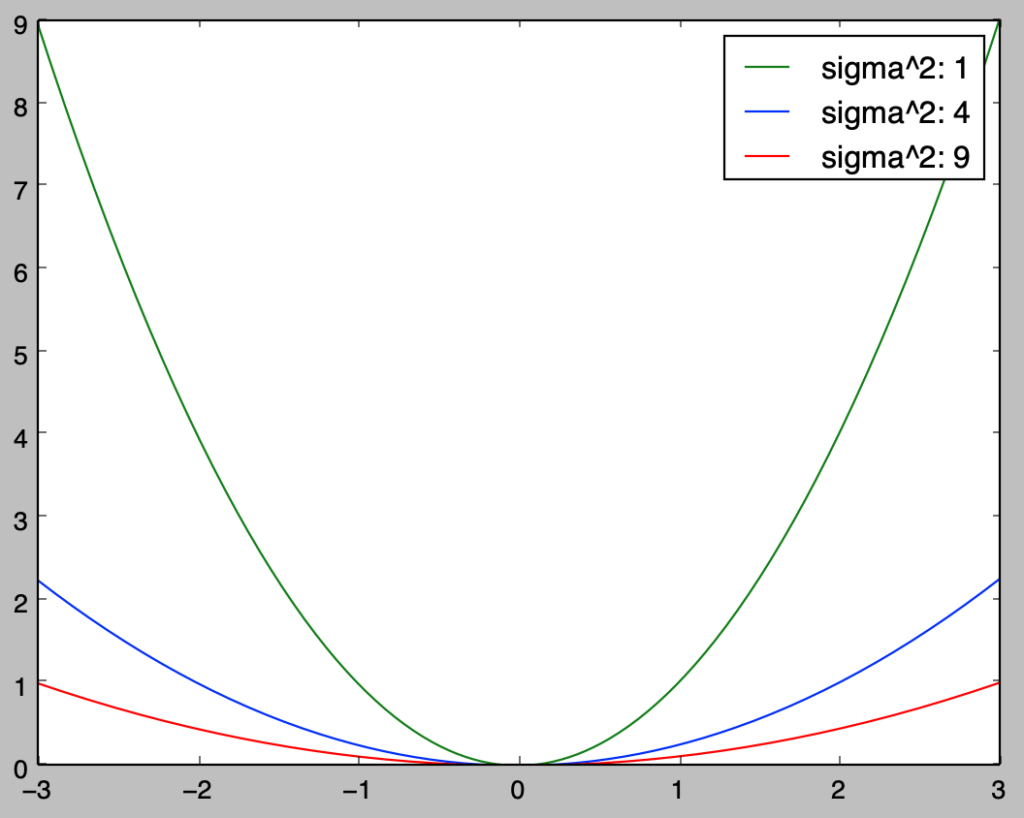
$\sigma^{2}=s^2$が成立するときのKLダイバージェンス$KL(p||q)$の値、$x$方向は$\Delta = \mu-m$の値、色は$\sigma^{2}=1$が緑、$\sigma^{2}=2^2$が青、$\sigma^{2}=3^2$が赤にそれぞれ対応
上の図より、「分散が同じ$2$つの正規分布のKLダイバージェンスは平均の差の$2$次関数で表され、分散の逆数が$y=ax^2$の$a$に対応する」ことが読み取れる。
平均が同一で分散を動かす場合
当項では$\mu=m$が成立するときに$KL(p||q)$が$\mu=m$の値に基づいてどのように変化するかに関して確認を行う。ここで$\sigma^2 = ks^2$とおくと、$(1)$式は下記のように変形できる。
$$
\large
\begin{align}
KL(p||q) &= \frac{1}{2} \left[ \ln{\frac{s^2}{\sigma^2}} + \frac{\sigma^2-s^2}{s^2} + \frac{(\mu-m)^2}{s^2} \right] \quad (1) \\
&= \frac{1}{2} \left[ \ln{\frac{s^2}{(ks)^2}} + \frac{(ks)^2-s^2}{s^2} + \frac{(m-m)^2}{s^2} \right] \\
&= \frac{1}{2} ( -\ln{k} + k – 1 )
\end{align}
$$
上記より、変数$k$に関するKLダイバージェンスのグラフ化は下記を実行することで行える。
import numpy as np
import matplotlib.pyplot as plt
k = np.arange(0.01,5.,0.01)
KL = (-np.log(k)+k-1)/2.
plt.plot(k,KL)
plt.show()・実行結果
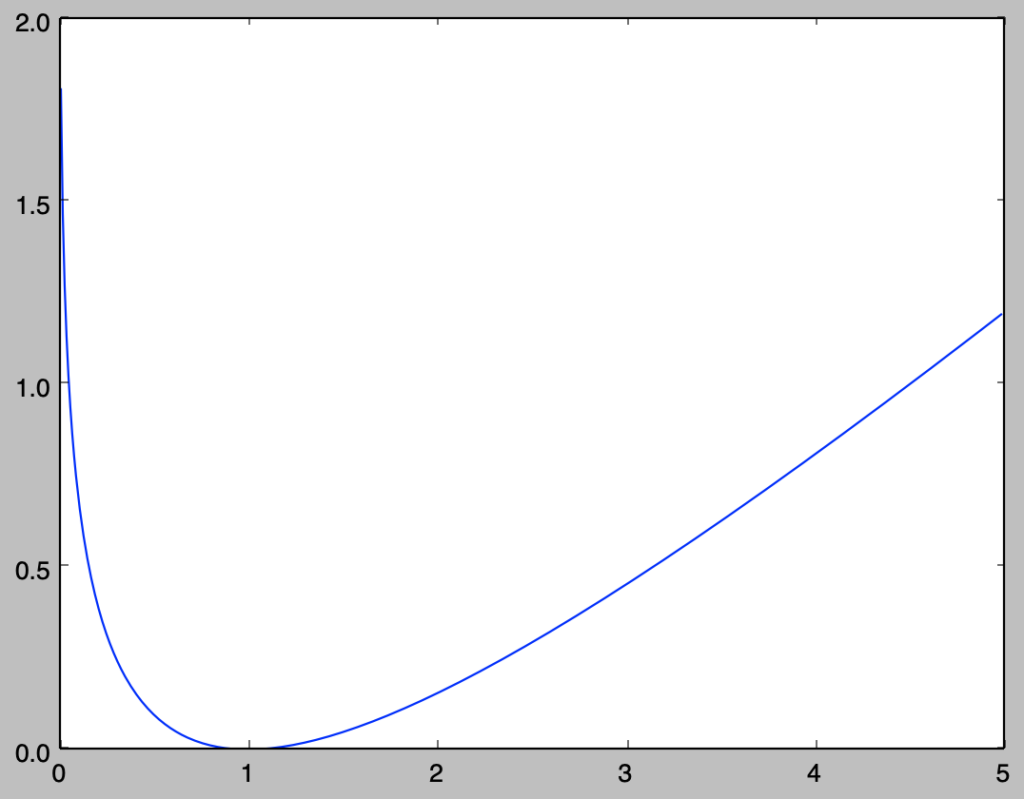
実行結果より$k=1$、すなわち$\sigma^2=s^2$が成立するときに$KL(p||q)=0$であることも合わせて確認できる。

[…] ・考察結果の解釈にあたって、下記でグラフ化などを取り扱った。https://www.hello-statisticians.com/explain-terms-cat/kl_divergence1.html […]