Ch.1 「序論」の章末問題の解答例　パターン認識と機械学習 1.21〜1.41

当記事は「パターン認識と機械学習」の読解サポートにあたってChapter.$1$の「序論」の章末問題の解説について行います。
基本的には書籍の購入者向けの解説なので、まだ入手されていない方は下記より入手をご検討ください。また、解説はあくまでサイト運営者が独自に作成したものであり、書籍の公式ページではないことにご注意ください。

・参考
パターン認識と機械学習 解答まとめ
https://www.hello-statisticians.com/answer_textbook#prml

解答まとめ

問題$1.21$

・$p(x,C_1) \geq p(x,C_2)$の区間$\mathcal{R}_{1}$
$$
\large
\begin{align}
p(x,C_2) \leq (p(x,C_1)p(x,C_2))^{\frac{1}{2}}
\end{align}
$$

・$p(x,C_1) < p(x,C_2)$の区間
$$
\large
\begin{align}
p(x,C_1) \leq (p(x,C_1)p(x,C_2))^{\frac{1}{2}}
\end{align}
$$

ここで$(1.78)$式に関して下記が成立する。
$$
\large
\begin{align}
p(\mathrm{mistake}) &= \int_{\mathcal{R}_{1}} p(x,C_2) dx + \int_{\mathcal{R}_{2}} p(x,C_1) dx \quad (1.78) \\
&= \int{\mathcal{R}_{1}} (p(x,C_1)p(x,C_2))^{\frac{1}{2}} dx + \int_{\mathcal{R}_{2}} (p(x,C_1)p(x,C_2))^{\frac{1}{2}} dx \\
& \leq \int (p(x,C_1)p(x,C_2))^{\frac{1}{2}} dx \quad (1.150)
\end{align}
$$

以上より$(1.150)$式は成立する。

問題$1.28$

$h(p^2)=h(p,p)=2h(p)$より$h(p^2)=2h(p)$が成立する。次に$h(p^k)=kh(p)$が成立するとき$h(p^{k+1})=(k+1)h(p)$が成立することを示す。
$$
\large
\begin{align}
h(p^{k+1}) &= h(p^{k},p) \\
&= h(p^{k}) + h(p) \\
&= kh(p) + h(p) = (k+1)h(p)
\end{align}
$$

上記より、数学的帰納法を用いることで任意の$n$に対し、$h(p^{n+1})=(n+1)h(p)$が成立する。また、このとき$p^{n/m}$に関して下記が成立する。
$$
\large
\begin{align}
h(p^{\frac{n}{m}}) &= n h(p^{\frac{1}{m}}) \\
&= \frac{n}{m} \times m h(p^{\frac{1}{m}}) \\
&= \frac{n}{m} h(p^{\frac{m}{m}}) = \frac{n}{m} h(p)
\end{align}
$$

以下、$h(p^{x})=xh(p)$が成立すると仮定するとき、$h(p) \propto \ln{p}$であることを示す。ここで$p=q^{x}$とおくと、$\displaystyle \frac{h(p)}{\ln{p}}$は下記のように変形を行える。
$$
\large
\begin{align}
\frac{h(p)}{\ln{p}} &= \frac{h(q^{x})}{\ln{q^{x}}} \\
&= \frac{\cancel{x}h(q)}{\cancel{x}\ln{q}} \\
&= \frac{h(q)}{\ln{q}}
\end{align}
$$

上記より$h(p) \propto \ln{p}$であることが示される。

問題$1.29$

$m$番目の状態の確率を$p(x_m)$で表すとき、全$M$状態に関するエントロピー$H[x]$は下記のように考えられる。
$$
\large
\begin{align}
H[x] = -\sum_{m=1}^{M} p(x_m) \ln{p(x_m)} = \sum_{m=1}^{M} p(x_m) \ln{\frac{1}{p(x_m)}}
\end{align}
$$

ここで$f(x) = \ln(x)$とおくと$f(x)$は上に凸の関数であるので、イェンセンの不等式を適用することで下記の変形が成立する。
$$
\large
\begin{align}
H[x] &= \sum_{m=1}^{M} p(x_m) \ln{\frac{1}{p(x_m)}} \\
& \leq \ln{ \sum_{m=1}^{M} p(x_m) \frac{1}{p(x_m)} } \\
&= \ln{ \sum_{m=1}^{M} 1} = \ln{M}
\end{align}
$$

問題$1.30$

$$
\large
\begin{align}
KL(p||q) &= – \int p(x) \ln{\frac{q(x)}{p(x)}} dx \quad (1.113) \\
&= \int p(x) \ln{p(x)} dx – \int p(x) \ln{q(x)} dx \quad (1)
\end{align}
$$

上記の$(1)$式の第$1$項は$(1.110)$式より下記のように表せる。
$$
\large
\begin{align}
\int p(x) \ln{p(x)} dx &= -H[x] \\
&= -\frac{1}{2} \left[ 1 + \ln{(2 \pi \sigma^2)} \right] \quad (1.110)
\end{align}
$$

上記の詳しい導出は演習$1.35$で取り扱った。また、$(1)$式の第$2$項は$q(x)=\mathcal{N}(x|m,s^{2})$より下記のように変形を行える。
$$
\large
\begin{align}
\int p(x) \ln{q(x)} dx &= \int p(x) \ln{\mathcal{N}(x|m,s^{2})} dx \\
&= \int p(x) \ln{ \left[ \frac{1}{\sqrt{2 \pi s^2}} \exp \left( -\frac{(x-m)^2}{2s^2} \right) \right]} dx \\
&= – \frac{1}{2} \ln{2 \pi s^2} \int p(x) dx – \frac{1}{2s^2} \int p(x)(x-m)^2 dx \quad (2)
\end{align}
$$

ここで$(2)$式を考えるにあたって、確率分布$p(x)=\mathcal{N}(x|\mu,\sigma^{2})$に関して下記が成立することを用いる。
$$
\large
\begin{align}
\int p(x) dx &= 1 \quad (1.48) \\
\int xp(x) dx &= \mu \quad (1.49) \\
\int x^2p(x) dx &= \mu^2+\sigma^2 \quad (1.50)
\end{align}
$$

上記の$(1.49),(1.50)$式の詳しい導出は演習$1.8$で取り扱った。$(1.48)$〜$(1.50)$を元に$(2)$式は下記のように変形を行える。
$$
\large
\begin{align}
& \int p(x) \ln{q(x)} dx \\
&= – \frac{1}{2} \ln{2 \pi s^2} \int p(x) dx – \frac{1}{2s^2} \int p(x)(x-m)^2 dx \quad (2) \\
&= – \frac{1}{2} \ln{2 \pi s^2} \int p(x) dx – \frac{1}{2s^2} \int p(x)(x^2-2mx+m^2) dx \\
&= – \frac{1}{2} \ln{2 \pi s^2} \int p(x) dx – \frac{1}{2s^2} \left[ \int x^2p(x) dx – 2m\int xp(x) dx + m^2 \int p(x) dx \right] \\
&= – \frac{1}{2} \ln{(2 \pi s^2)} – \frac{1}{2s^2} \left[ \mu^2+\sigma^2 – 2 \mu m + m^2 \right] \quad (3)
\end{align}
$$

$(1)$式に$(1.110)$式と$(3)$式を代入することで下記が得られる。
$$
\large
\begin{align}
KL(p||q) &= \int p(x) \ln{p(x)} dx – \int p(x) \ln{q(x)} dx \quad (1) \\
&= -\frac{1}{2} \left[ 1 + \ln{(2 \pi \sigma^2)} \right] + \frac{1}{2} \ln{(2 \pi s^2)} + \frac{1}{2s^2} \left[ \mu^2+\sigma^2 – 2 \mu m + m^2 \right] \\
&= \frac{1}{2} \ln{\frac{\cancel{2 \pi} s^2}{\cancel{2 \pi} \sigma^2}} + \frac{1}{2s^2} \left[ \mu^2+\sigma^2 – 2 \mu m + m^2 \right] – \frac{1}{2} \\
&= \frac{1}{2} \ln{\frac{s^2}{\sigma^2}} + \frac{1}{2} \left[ \frac{1}{s^2}(\mu^2+\sigma^2 – 2 \mu m + m^2) – 1 \right] \\
&= \ln{\frac{s}{\sigma}} + \frac{1}{2} \left[ \frac{1}{s^2}(\mu^2+\sigma^2 – 2 \mu m + m^2) – 1 \right]
\end{align}
$$

・考察
結果の解釈にあたって、下記でグラフ化などを取り扱った。
https://www.hello-statisticians.com/explain-terms-cat/kl_divergence1.html

問題$1.31$

$H[x,y]$は下記のように変形を行える。
$$
\large
\begin{align}
H[x,y] &= H[y|x] + H[x] \quad (1.112) \\
&= H[y|x] – H[y] + H[x] + H[y] \\
&= I[x,y] + H[x] + H[y] \quad (1.121) \\
&= \mathrm{KL}(p(x,y)||p(x)p(y)) + H[x] + H[y] \quad (1.120) \\
& \geq H[x] + H[y]
\end{align}
$$

上記の不等号は$KL$ダイバージェンスが$0$以上であることを元に成立する。また、$KL$ダイバージェンスの等号の成立条件は$p(x,y)=p(x)p(y)$であるので、「$p(x,y)=p(x)p(y)$が成立する」すなわち$x, y$が独立の場合は等号が成立する。

問題$1.35$

$(1.104)$式に$(1.109)$式を代入すると、下記のように変形を行える。
$$
\large
\begin{align}
H[x] &= – \int p(x) \ln p(x) dx \quad (1.104) \\
&= – \int p(x) \ln \left[ -\frac{1}{\sqrt{2 \pi \sigma^2}} \exp \left( -\frac{(x-\mu)^2}{2 \sigma^2} \right) \right] dx \\
&= – \int p(x) \left( -\frac{(x-\mu)^2}{2 \sigma^2} – \frac{1}{2} \ln{(2 \pi \sigma^2)} \right) dx \\
&= \frac{1}{2 \sigma^2} \int p(x) (x-\mu)^2 dx + \frac{1}{2} \ln{(2 \pi \sigma^2)} \int p(x) dx \\
&= \frac{1}{2 \sigma^2} \times \sigma^2 + \frac{1}{2} \ln{(2 \pi \sigma^2)} \int p(x) dx \\
&= \frac{1}{2} \left[ 1 + \ln{(2 \pi \sigma^2)} \right] \quad (1.110)
\end{align}
$$

上記の途中計算では$(1.106)$式と$(1.107)$を用いた。

・考察
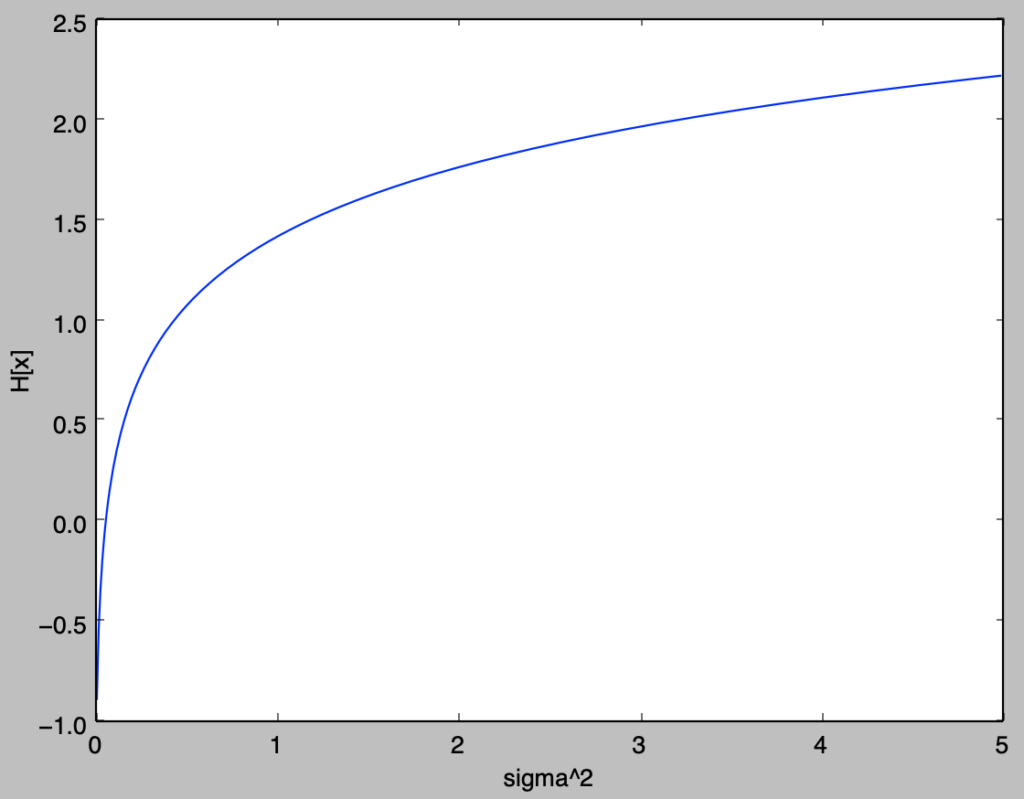
$\sigma^2$の値の変化に対して$H[x]$がどのように変化するかを以下確認する。

import numpy as np
import matplotlib.pyplot as plt

sigma2 = np.arange(0.01,5.,0.01)
h_x = (1+np.log(2*np.pi*sigma2))/2.

plt.plot(sigma2,h_x)
plt.xlabel("sigma^2")
plt.ylabel("H[x]")

plt.show()

・実行結果

問題$1.36$

$2$階微分は$1$階微分の増減を表すので、$2$階微分が正である場合は$1$階微分が単調増加となる。$1$階微分が単調増加の場合、弦$\geq$関数となり、下に凸の定義と一致する。より厳密な証明は平均値の定理などを用いて行うことができるが直感的な理解を重視するにあたってここでは省略する。

問題$1.37$

$H[\mathbf{x},\mathbf{y}]$はエントロピーの定義より下記のように表される。
$$
\large
\begin{align}
H[\mathbf{x},\mathbf{y}] = – \int \int p(\mathbf{x},\mathbf{y}) \ln{p(\mathbf{x},\mathbf{y})} dy dx
\end{align}
$$

ここで$p(\mathbf{x},\mathbf{y}) = p(\mathbf{y}|\mathbf{x})p(\mathbf{x})$が成立するので$\ln{p(\mathbf{x},\mathbf{y})}$は下記のように変形することができる。
$$
\large
\begin{align}
\ln{p(\mathbf{x},\mathbf{y})} &= \ln{p(\mathbf{y}|\mathbf{x})p(\mathbf{x})} \\
&= \ln{p(\mathbf{y}|\mathbf{x})} + \ln{p(\mathbf{x})}
\end{align}
$$

よって$H[\mathbf{x},\mathbf{y}]$は下記のように変形することができる。
$$
\large
\begin{align}
H[\mathbf{x},\mathbf{y}] &= – \int \int p(\mathbf{x},\mathbf{y}) \ln{p(\mathbf{x},\mathbf{y})} dy dx \\
&= – \int \int p(\mathbf{x},\mathbf{y}) (\ln{p(\mathbf{y}|\mathbf{x})} + \ln{p(\mathbf{x})}) dy dx \\
&= – \int \int p(\mathbf{x},\mathbf{y}) \ln{p(\mathbf{y}|\mathbf{x})} dy dx – \int \int p(\mathbf{x},\mathbf{y}) \ln{p(\mathbf{x})} dy dx \\
&= H[\mathbf{y}|\mathbf{x}] – \int \int p(\mathbf{x}) \ln{p(\mathbf{x})} dx \\
&= H[\mathbf{y}|\mathbf{x}] + H[\mathbf{x}]
\end{align}
$$

上記より$(1.112)$式が成立する。

問題$1.38$

$$
\large
\begin{align}
f \left( \sum_{i=1}^{M} \lambda_{i} x_{i} \right) \leq \sum_{i=1}^{M} f(x_{i}) \quad (1.115)
\end{align}
$$

上記に表した$(1.115)$式を以下数学的帰納法を用いて示す。具体的には「i) $M=2$で成立」、「ⅱ) $M=k$で成立すれば$M=k+1$で成立」を示せば良い。i)は$(1.114)$式が対応するので、ⅱ)に関して下記で示す。

$$
\large
\begin{align}
f \left( \sum_{i=1}^{M+1} \lambda_{i} x_{i} \right) &= f \left( \lambda_{M+1} x_{M+1} + \sum_{i=1}^{M} \lambda_{i} x_{i} \right) \\
&= f \left( \lambda_{M+1} x_{M+1} + (1-\lambda_{M+1})\sum_{i=1}^{M} \frac{\lambda_{i}}{1-\lambda_{M+1}} x_{i} \right) \\
& \leq \lambda_{M+1} f(x_{M+1}) + (1-\lambda_{M+1}) f \left( \sum_{i=1}^{M} \frac{\lambda_{i}}{1-\lambda_{M+1}} x_{i} \right) \quad (1)
\end{align}
$$

ここで上記の式で$\displaystyle \sum_{i=1}^{k} \frac{\lambda_{i}}{1-\lambda_{k+1}} = \frac{1-\lambda_{k+1}}{1-\lambda_{k+1}} = 1$より下記が成立する。
$$
\large
\begin{align}
f \left( \sum_{i=1}^{k} \frac{\lambda_{i}}{1-\lambda_{k+1}} x_{i} \right) \leq \sum_{i=1}^{k}\frac{\lambda_{i}}{1-\lambda_{k+1}} f(x_{i}) \quad (2)
\end{align}
$$

$(1)$式と$(2)$式より下記が成立する。
$$
\large
\begin{align}
f \left( \sum_{i=1}^{k+1} \lambda_{i} x_{i} \right) & \leq \lambda_{k+1} f(x_{k+1}) + (1-\lambda_{k+1}) f \left( \sum_{i=1}^{k} \frac{\lambda_{i}}{1-\lambda_{k+1}} x_{i} \right) \\
& \leq \lambda_{k+1} f(x_{k+1}) + (1-\lambda_{k+1}) \sum_{i=1}^{k} \frac{\lambda_{i}}{1-\lambda_{k+1}} f(x_{i}) \\
&= \lambda_{k+1} f(x_{k+1}) + \sum_{i=1}^{k} \lambda_{i} f(x_{i}) = \sum_{i=1}^{k+1} \lambda_{i} f(x_{i})
\end{align}
$$

上記よりⅱ)が示される。よってi)とⅱ)が成立することより、$(1.115)$式は任意の$M \geq 2$で成立することが示される。

問題$1.40$

$$
\large
\begin{align}
\frac{1}{n} \sum_{i=1}^{n} x_n \geq \left( \prod_{i=1}^{n} x_n \right)^{\frac{1}{n}} \quad (1)
\end{align}
$$

上記の$(1)$式が成立することを示せば良いので、$\displaystyle \ln{\left( \prod_{i=1}^{n} x_n \right)^{\frac{1}{n}}} \leq \ln{ \left[ \frac{1}{n} \sum_{i=1}^{n} x_n \right] }$を示すことを考える。

$\displaystyle \ln{\left( \prod_{i=1}^{n} x_n \right)^{\frac{1}{n}}}$を下記のように変形し、イェンセンの不等式を適用することを考える。
$$
\large
\begin{align}
\ln{\left( \prod_{i=1}^{n} x_n \right)^{\frac{1}{n}}} &= \frac{1}{n} \ln{\left( \prod_{i=1}^{n} x_n \right)} \\
&= \frac{1}{n} \sum_{i=1}^{n} \ln{x_n} \\
&= \sum_{i=1}^{n} \frac{1}{n} \ln{x_n} \\
& \leq \ln{ \left[ \sum_{i=1}^{n} \frac{1}{n} x_n \right] } \\
&= \ln{ \left[ \frac{1}{n} \sum_{i=1}^{n} x_n \right] }
\end{align}
$$

上記より$(1)$式が成立することが示せる。

問題$1.41$

$(1.120)$式は下記のように変形を行える。
$$
\large
\begin{align}
I[x,y] &= \mathrm{KL}(p(x,y)||p(x)p(y)) = – \int \int p(x,y) \ln{ \left( \frac{p(x)p(y)}{p(x,y)} \right) } dx dy \quad (1.120) \\
&= \int \int p(x,y) \left( \ln{p(x)} + \ln{\frac{p(y)}{p(x,y)}} \right) dx dy \\
&= – \int \int p(x,y) \left( \ln{p(x)} – \ln{\frac{p(x,y)}{p(y)}} \right) dx dy \\
&= – \int \int p(x,y) \ln{p(x)} dx dy + \int \int p(x,y) \ln{p(x|y)} dx dy \\
&= H[x] – H[x|y] \quad (1.121)’
\end{align}
$$

上記より$I[x,y]=H[x]-H[x|y]$が成立する。また同様に考えることで$I[x,y]=H[y]-H[y|x]$も示すことができ、$(1.121)$式が成立することがわかる。