あつまれ統計の森

Hello Statisticians!

基底関数の集合に対応するカーネル関数の計算とPythonを用いたグラフの作成

投稿日: 投稿者: lib-arts

カーネル法(Kernel methods)の理解にあたって、計算処理の概要が把握しにくいように思われたので、Pythonプログラムの作成を通して図などの再現を行います。当記事では「パターン認識と機械学習」の下巻の$6.2$節の「カーネル関数の構成」を元に、図$6.1$の再現をPythonを用いて行いました。

英語版と翻訳版で図に相違がありましたが、翻訳版の図の再現を目標に作成を行いました。

また、$(\mathrm{o.xx})$の形式の式番号は「パターン認識と機械学習」の式番号に対応させました。

パターン認識と機械学習 下 (ベイズ理論による統計的予測)

パターン認識と機械学習 下 (ベイズ理論による統計的予測)

C.M. ビショップ
8,580円(03/27 04:09時点)
Amazon

・参考
演習の解答：パターン認識と機械学習

前提の確認

カーネル関数の数式

$$
\large
\begin{align}
k(x,x’) = \boldsymbol{\phi}(x)^{\mathrm{T}}\boldsymbol{\phi}(x’) = \sum_{i=1}^{M} \phi_{i}(x)\phi_{i}(x’) \quad (6.10)
\end{align}
$$

図$6.1$は、上記で表した$(6.10)$式に基づいて作成される。ここで$(6.10)$の$x$と$x’$はスカラー、$\phi_{i}(x)$はスカラー関数である一方で、$\boldsymbol{\phi}(x)$はベクトルを表すことに注意が必要である。ここでスカラー$x$に対して$\boldsymbol{\phi}(x)$がベクトルを表すというのは、$x,x^2,…,x^M$のように多項式を考えるなど、表現方法がいくつかある。また、$x’$は$x$と対になる点であり、カーネル関数は$x$と$x’$の類似度を主に表すと大まかに掴んでおくとよい。

具体的には多項式を元に$x,…,x^{M}$のように基底関数を考えると、$(6.10)$式のカーネル関数は下記のように表せる。
$$
\large
\begin{align}
k(x,z) &= \boldsymbol{\phi}(x)^{\mathrm{T}}\boldsymbol{\phi}(z) \\
&= \left(\begin{array}{ccccc} x & x^{2} & \cdots & x^{M-1} & x^{M} \end{array} \right) \left(\begin{array}{c} z \\ z^{2} \\ \vdots \\ z^{M-1} \\ z^{M} \end{array} \right) \\
&= \sum_{m=1}^{M} x^{m}z^{m}
\end{align}
$$

$x’$の$M$乗を$(x’)^{M}$表すと表記が難しくなるので上記では$x’$ではなく$z$を用いた。上記では$x$と$z$がスカラーであるのに対して、$\boldsymbol{\phi}(x),\boldsymbol{\phi}(z)$がベクトルであることが確認できる。

基底関数

Pythonを用いたカーネル関数の計算

当節ではPythonを用いたカーネル関数の計算を行う。当節では$(6.10)$式の解釈が行いやすいように$x$がスカラーである前提で関数の作成を行なったことで計算効率が良くないので、次節で計算の簡略化に関して取り扱う。

基底関数が多項式関数である場合

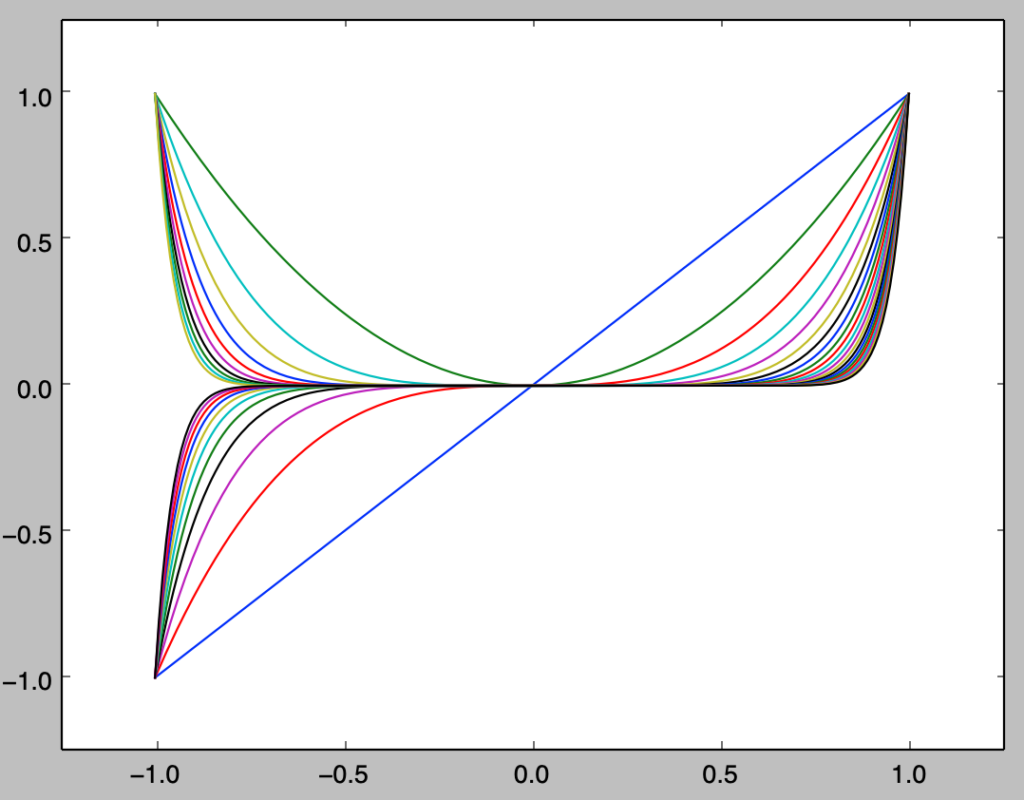
当項では基底関数が多項式関数である場合のカーネル関数の計算を行う。よって図$6.1$の左の図の再現を行う。

まずは基底関数に関して図示を行う。

import numpy as np
import matplotlib.pyplot as plt

def basis_poly(x,n):
    res = np.zeros(n)
    res[0] = x
    for i in range(1,n):
        res[i] = res[i-1]*x
    return res

n = 21
x = np.arange(-1.,1.01,0.01)

phi = np.zeros([x.shape[0],n])
for i in range(x.shape[0]):
    phi[i,:] = basis_poly(x[i],n)

for i in range(n):
    plt.plot(x,phi[:,i])

plt.xlim([-1.25,1.25])
plt.ylim([-1.25,1.25])
plt.show()

・実行結果

「パターン認識と機械学習」の図$6.1$の左上に対応

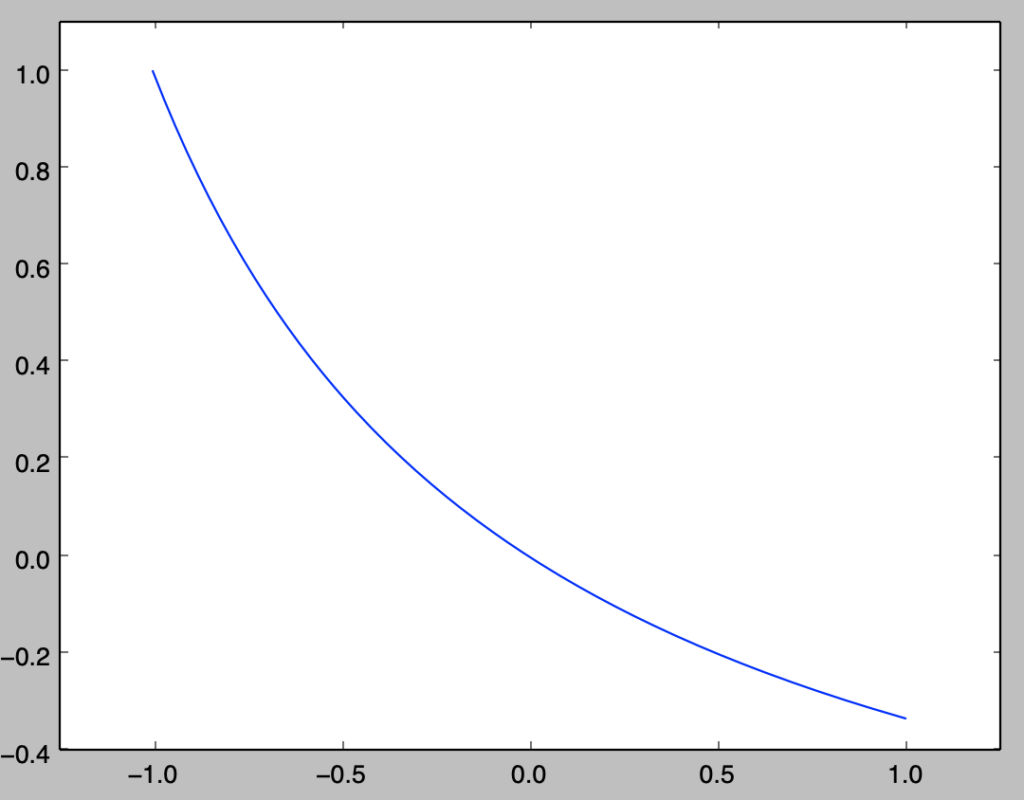
上記のように表した基底関数を元に、下記を実行することで$x’=-0.5$のときのカーネル関数の計算を行える。

k = np.zeros(x.shape[0])

for i in range(x.shape[0]):
    k[i] = np.dot(basis_poly(x[i],n),basis_poly(-0.5,n))

plt.plot(x,k)

plt.xlim([-1.25,1.25])
plt.ylim([-0.4,1.1])
plt.show()

・実行結果

「パターン認識と機械学習」の図$6.1$の左下に対応

基底関数がガウス分布である場合

ガウス分布に基づく基底関数に関して図示を行う。

import numpy as np
import matplotlib.pyplot as plt
from scipy import stats

def basis_norm(x,odd_n,sigma):
    res = np.zeros(odd_n)
    for i in range(odd_n):
        res[i] = stats.norm.pdf(x,loc=2*i/np.float(odd_n-1)-1.,scale=sigma)
    return res

odd_n = 21
sigma = 0.2
x = np.arange(-1.,1.01,0.01)

phi = np.zeros([x.shape[0],odd_n])
for i in range(x.shape[0]):
    phi[i,:] = basis_norm(x[i],odd_n,sigma)

for i in range(odd_n):
    plt.plot(x,phi[:,i])

plt.xlim([-1.25,1.25])
plt.show()

・実行結果

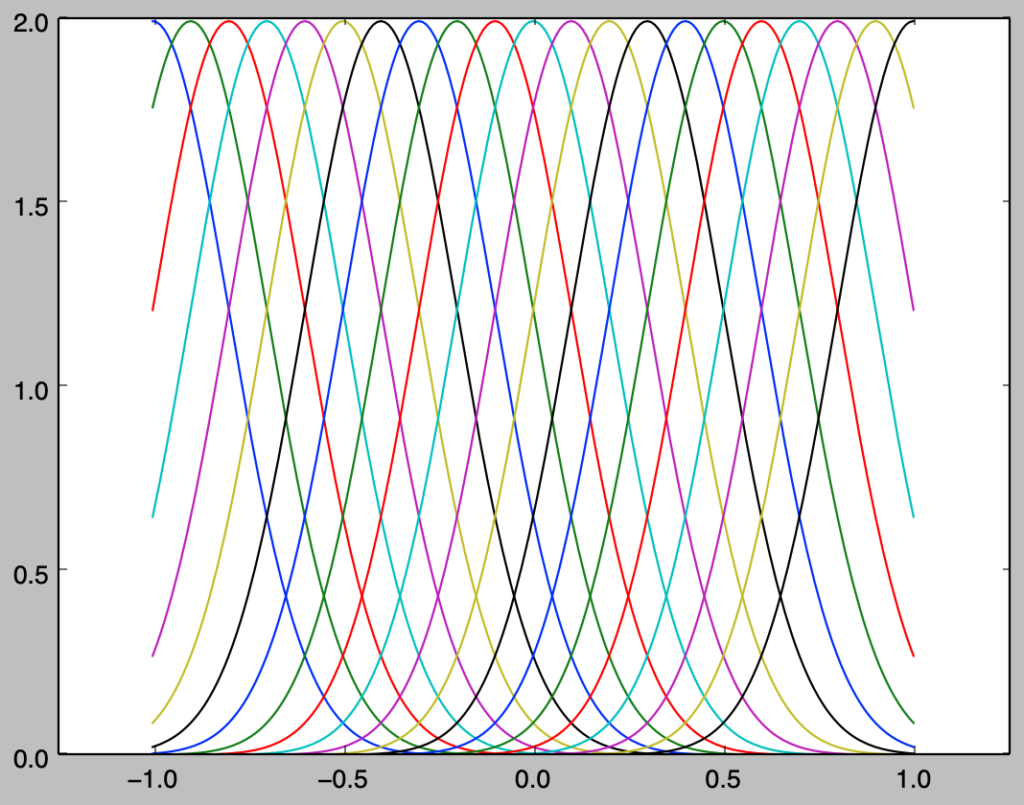
「パターン認識と機械学習」の図$6.1$の中央上に対応

上記のように表した基底関数を元に、下記を実行することで$x’=0$のときのカーネル関数の計算を行える。

k = np.zeros(x.shape[0])

for i in range(x.shape[0]):
    k[i] = np.dot(basis_norm(x[i],odd_n,sigma),basis_norm(0.,odd_n,sigma))

plt.plot(x,k)
plt.xlim([-1.25,1.25])
plt.show()

・実行結果

「パターン認識と機械学習」の図$6.1$の中央下に対応

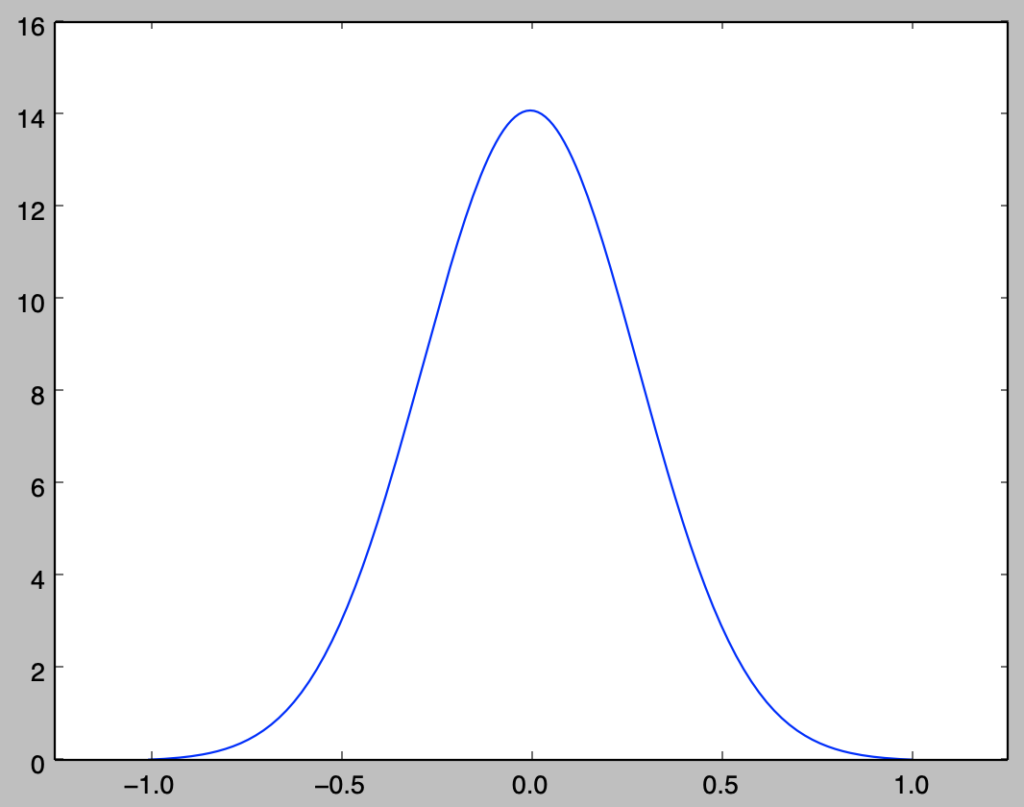
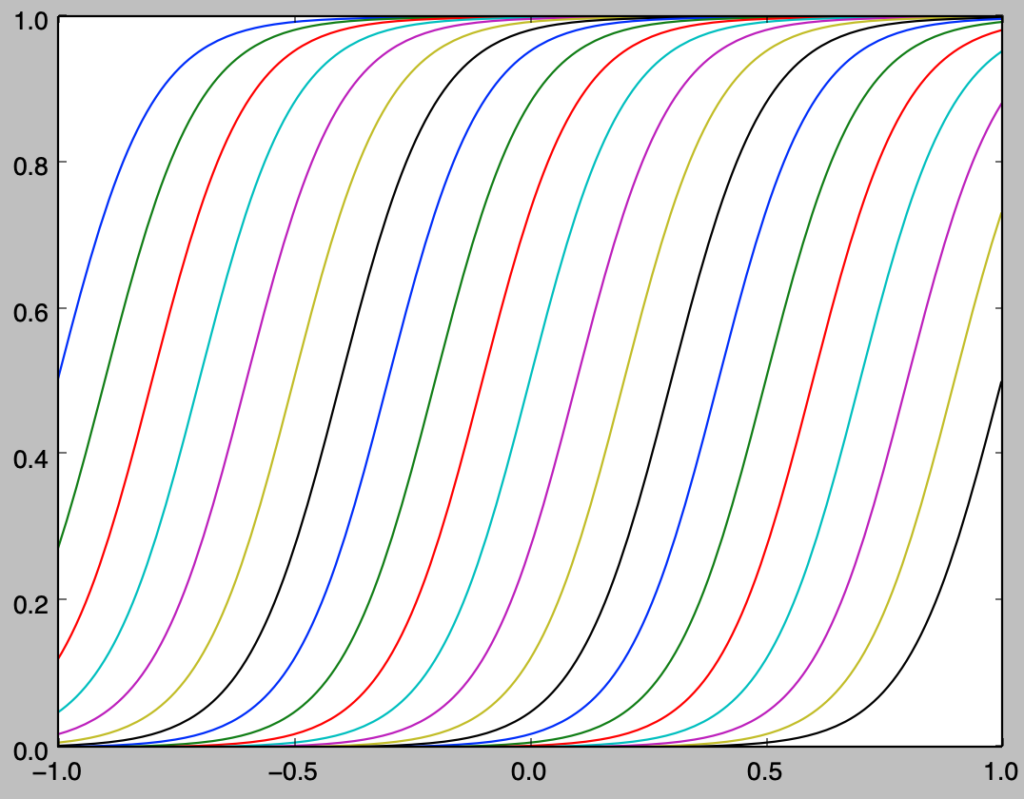
基底がシグモイド関数である場合

シグモイド関数に基づく基底関数に関して図示を行う。

import numpy as np
import matplotlib.pyplot as plt

def basis_sigmoid(x,odd_n,slope):
    res = np.zeros(odd_n)
    for i in range(odd_n):
        a = 2*i/np.float(odd_n-1)-1.
        res[i] = 1./(1.+np.exp(-slope*(x-a)))
    return res

odd_n = 21
slope = 10.
x = np.arange(-1.,1.01,0.01)

phi = np.zeros([x.shape[0],odd_n])
for i in range(x.shape[0]):
    phi[i,:] = basis_sigmoid(x[i],odd_n,slope)

for i in range(odd_n):
    plt.plot(x,phi[:,i])

plt.xlim([-1.,1.])
plt.show()

・実行結果

「パターン認識と機械学習」の図$6.1$の右上に対応

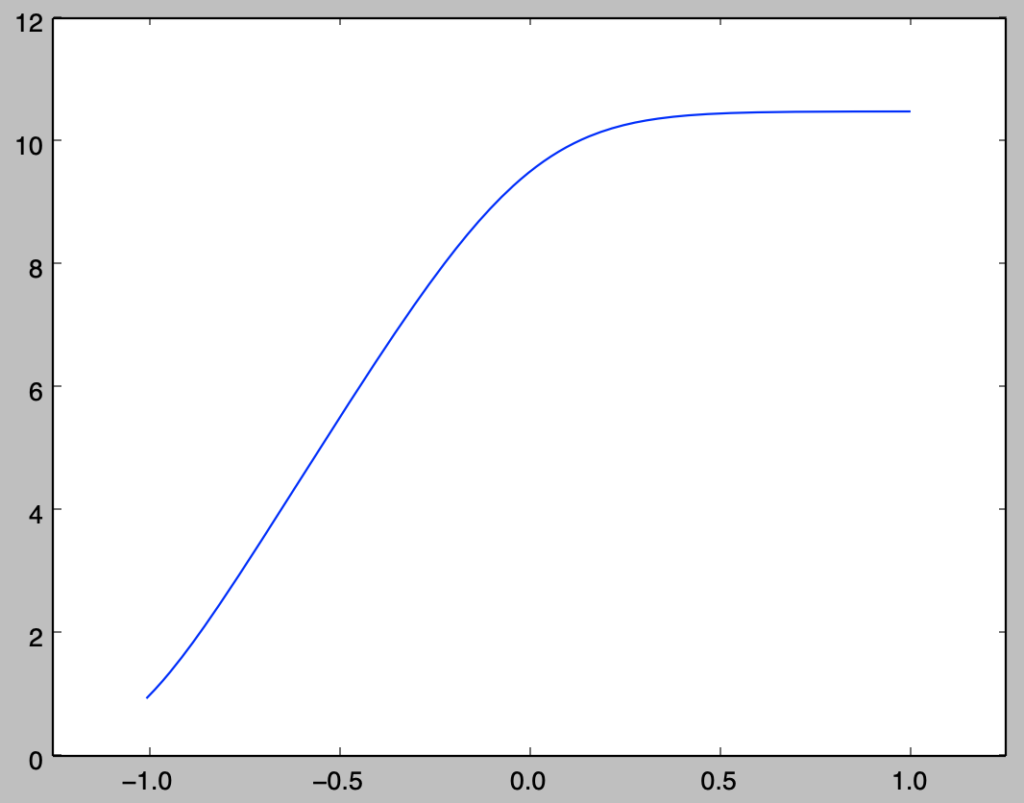
上記のように表した基底関数を元に、下記を実行することで$x’=0$のときのカーネル関数の計算を行える。

k = np.zeros(x.shape[0])

for i in range(x.shape[0]):
    k[i] = np.dot(basis_sigmoid(x[i],odd_n,slope),basis_sigmoid(0.,odd_n,slope))

plt.plot(x,k)
plt.xlim([-1.25,1.25])
plt.show()

・実行結果

「パターン認識と機械学習」の図$6.1$の右下に対応

処理の高速化

以下、多項式関数に基づいて基底を設定した例に基づいて処理の効率化を行う。

基底に関する処理のベクトル化

前節で作成を行なったbasis_polyはスカラーを受け取る形式でプログラムの作成を行なったが、$x$の値の変化に対してグラフ作成を行う際の処理全体を俯瞰すると効率が良くなかった。以下ではbasis_polyがベクトルを受け取り行列を返すように修正を行う。

import numpy as np
import matplotlib.pyplot as plt

def basis_poly(x,n):
    res = np.zeros([x.shape[0],n])
    res[:,0] = x
    for i in range(1,n):
        res[:,i] = res[:,i-1]*x
    return res

n = 21
x = np.arange(-1.,1.01,0.01)

phi = basis_poly(x,n)

for i in range(n):
    plt.plot(x,phi[:,i])

plt.xlim([-1.25,1.25])
plt.ylim([-1.25,1.25])
plt.show()

・実行結果

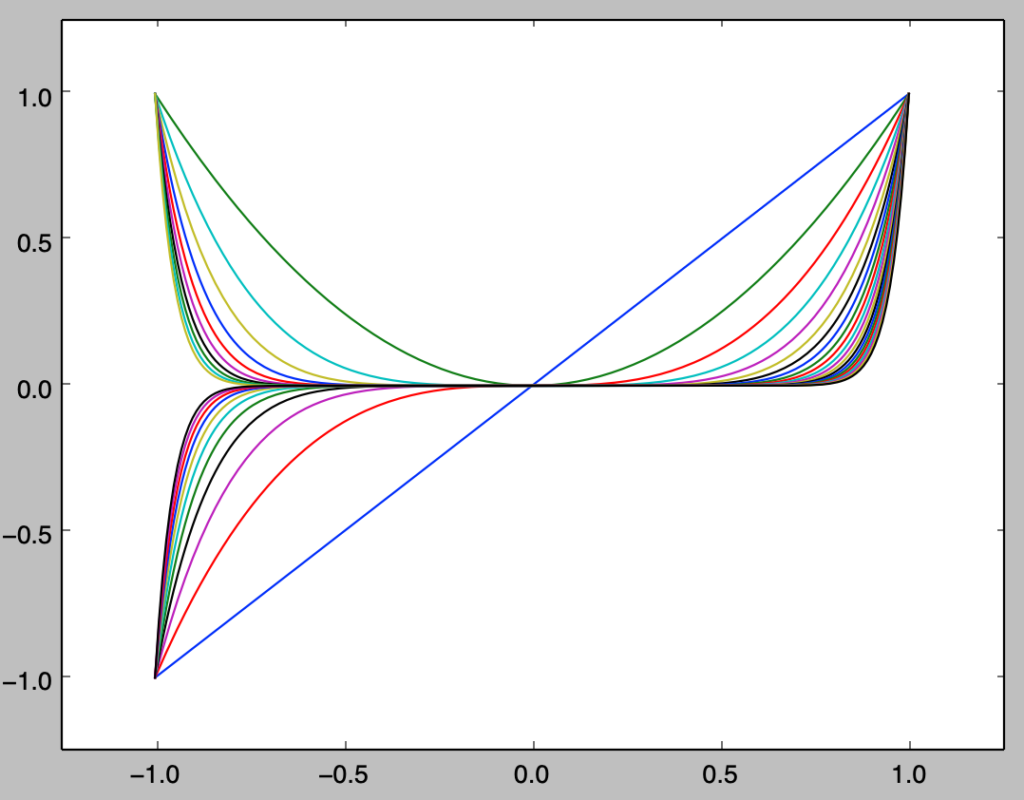
上記は前節の結果と同様である。また、カーネル関数は下記のように計算を行える。

k = np.zeros(x.shape[0])

for i in range(x.shape[0]):
    k[i] = np.dot(phi[i,:],basis_poly(np.array([-0.5]),n)[0,:])

plt.plot(x,k)

plt.xlim([-1.25,1.25])
plt.ylim([-0.4,1.1])
plt.show()

・実行結果

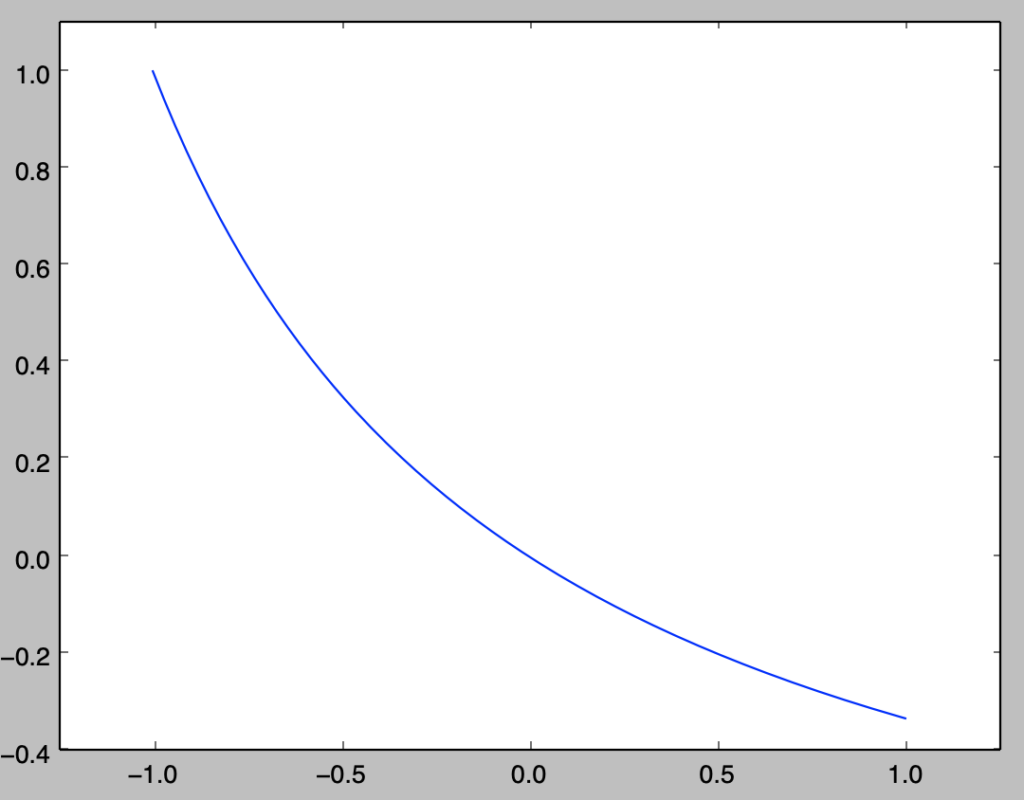
上記の結果も前節の結果と同様である。また、上記の計算にあたってbasis_poly(np.array([-0.5]),n)[0,:]のようにスカラーを入力してベクトルを出力すれば十分な場合にbasis_polyはやや冗長であるので、basis_poly内で場合分けすると良い。

一方で、ここで取り扱ったのは処理の流れの把握用のプログラムであるので、あえてbasis_poly内のプログラムを増やさずに外部からの制御を行う形式で作成を行なった。

「基底関数の集合に対応するカーネル関数の計算とPythonを用いたグラフの作成」への2件のフィードバック

コメントは受け付けていません。