ガウス過程回帰の導出の流れとPythonプログラムを用いた$2 \sigma$区間の作成

実際に観測されるサンプルを$(\mathbf{x}_1,t_1), …, (\mathbf{x}_N,t_N)$とおくとき、実測値$t_n$と予測値$t_n$に関して下記が成立すると考える。
$$
\large
\begin{align}
t_n = y_n + \epsilon_n \\
\epsilon_n \sim \mathcal{N}(0,\sigma^2)
\end{align}
$$

このとき条件付き確率$p(t_n|y_n)$は上記に基づいて下記のように表すことができる。
$$
\large
\begin{align}
p(t_n|y_n) = \mathcal{N}(y_n,\sigma^2)
\end{align}
$$

上記を$N$個のサンプルに関して考えると下記が成立する。
$$
\large
\begin{align}
p(\mathbf{t}|\mathbf{y}) &= \mathcal{N}(\mathbf{y},\sigma^2 I_N) \\
\mathbf{t} &= \left( \begin{array}{c} t_{1} \\ \vdots \\ t_{N} \end{array} \right) \\
\mathbf{y} &= \left( \begin{array}{c} y_{1} \\ \vdots \\ y_{N} \end{array} \right)
\end{align}
$$

また、前項の$\mathbf{y} \sim \mathcal{N}(\mathbf{0},\lambda^2 \boldsymbol{\Phi} \boldsymbol{\Phi}^{\mathrm{T}})$より、$p(\mathbf{y})$は下記のように表せる。
$$
\large
\begin{align}
p(\mathbf{y}) = \mathcal{N}(\mathbf{0},\lambda^2 \boldsymbol{\Phi} \boldsymbol{\Phi}^{\mathrm{T}})
\end{align}
$$

このとき、周辺分布$p(\mathbf{t})$は下記のように考えることができる。
$$
\large
\begin{align}
p(\mathbf{t}) = \int p(\mathbf{t}|\mathbf{y}) p(\mathbf{y}) d \mathbf{y}
\end{align}
$$

上記に対して「多次元正規分布におけるベイズの定理を用いた周辺確率の導出」で取り扱った結果を元に考えると、$p(\mathbf{t})$は下記のように表せる。
$$
\large
\begin{align}
p(\mathbf{t}) &= \int p(\mathbf{t}|\mathbf{y}) p(\mathbf{y}) d \mathbf{y} \\
&= \mathcal{N}(\mathbf{0},C) \quad (6.61) \\
C &= \sigma^2 I_N + \lambda^2 \boldsymbol{\Phi} \boldsymbol{\Phi}^{\mathrm{T}} = \sigma^2 I_N + K \quad (6.62)’
\end{align}
$$

上記の$K$はグラム行列に一致し、「カーネル関数」に基づいて計算できる。上記は$\mathbf{t}$に関する同時分布であるが、ここで新たなサンプルの$\mathbf{x}_{N+1}$が得られたとき、下記で定める$\mathbf{t}_{N+1}$に関する同時分布を新たに考える。
$$
\large
\begin{align}
\mathbf{t}_{N+1} &= \left( \begin{array}{c} t_{1} \\ t_{2} \\ \vdots \\ t_{N} \\ t_{N+1} \end{array} \right)
\end{align}
$$

ここで同時分布$p(\mathbf{t}_{N+1})$は$(6.61)$に基づいて下記のように得られると考える。
$$
\large
\begin{align}
p(\mathbf{t}_{N+1}) &= \mathcal{N}(\mathbf{0},C_{N+1}) \quad (6.64)
\end{align}
$$

ここで$C_{N+1}$の$(i,j)$成分を$(C_{N+1})_{ij}$とおくと、$(C_{N+1})_{ij}$は「カーネル関数」$k(\mathbf{x},\mathbf{x}’)$を用いて$(C_{N+1})_{ij} = \sigma^2 (I_{N})_{ij} + k(\mathbf{x}_{i},\mathbf{x}_{j})$のように計算できる。

同時分布の条件付き分布の計算による予測分布の導出

前項で計算を行なった$p(\mathbf{t}_{N+1}) = \mathcal{N}(\mathbf{0},C_{N+1})$に対して、条件付き分布$p(t_{N+1}|\mathbf{t})$を導出することを当項では考える。前項の同時分布$p(\mathbf{t}_{N+1})$に関して下記のような式表記を定める。
$$
\large
\begin{align}
p(\mathbf{t}_{N+1}) &= \mathcal{N}(\mathbf{0},C_{N+1}) \quad (6.64) \\
C_{N+1} &= \left( \begin{array}{cc} C_{N} & \mathbf{k} \\ \mathbf{k}^{\mathrm{T}} & c \end{array} \right) \quad (6.65) \\
(C_{N+1})_{ij} &= \sigma^2 (I_{N+1})_{ij} + k(\mathbf{x}_{i},\mathbf{x}_{j}) \quad (6.62)^{”}
\end{align}
$$

上記に対し、多次元正規分布の条件付き確率に関する$(2.81),(2.82)$式を用いることで、$p(t_{N+1}|\mathbf{t})$が下記のように導出できる。
$$
\large
\begin{align}
p(t_{N+1}|\mathbf{t}) = \mathcal{N}(\mathbf{k}^{\mathrm{T}}C_{N}^{-1}\mathbf{t}, c-\mathbf{k}^{\mathrm{T}}C_{N}^{-1}\mathbf{k}) \quad (6.66), (6.67)
\end{align}
$$

なお、多次元正規分布の条件付き確率に関する$(2.81),(2.82)$式の導出は下記で詳しく取り扱った。

多次元正規分布における条件付き確率分布の数式の導出を理解する

また、式の適用の詳細に関しては「パターン認識と機械学習」の演習$6.20$の解答で取りまとめた。

予測値が複数の場合の予測分布の作成

$M$個の予測値を表すにあたって、下記のように$\mathbf{t}_{M},\mathbf{t}_{N+M}$を定める。
$$
\large
\begin{align}
\mathbf{t}_{M} &= \left( \begin{array}{c} t_{1} \\ \vdots \\ t_{M} \end{array} \right) \\
\mathbf{t}_{N+M} &= \left( \begin{array}{c} t_{1} \\ \vdots \\ t_{N} \\ t_{N+1} \\ \vdots \\ t_{N+M} \end{array} \right)
\end{align}
$$

上記に対して、同時分布$p(\mathbf{t}_{N+M})$を下記のように表すことを考える。
$$
\large
\begin{align}
p(\mathbf{t}_{N+M}) &= \mathcal{N}(\mathbf{0},C_{N+M}) \\
C_{N+M} &= \left( \begin{array}{cc} C_{N} & \mathbf{k}_2 \\ \mathbf{k}_2^{\mathrm{T}} & C_{M} \end{array} \right) \\
(C_{N+M})_{ij} &= \sigma^2 (I_{N+M})_{ij} + k(\mathbf{x}_{i},\mathbf{x}_{j})
\end{align}
$$

上記の同時分布$\mathbf{t}_{N+M}$に、多次元正規分布の条件付き確率に関する$(2.81),(2.82)$式を用いることで、$p(\mathbf{t}_{M}|\mathbf{t})$が下記のように導出できる。
$$
\large
\begin{align}
p(\mathbf{t}_{M}|\mathbf{t}) = \mathcal{N}(\mathbf{k}_2^{\mathrm{T}}C_{N}^{-1}\mathbf{t}, C_{M}-\mathbf{k}_2^{\mathrm{T}}C_{N}^{-1}\mathbf{k}_2) \quad (6.66)’, (6.67)’
\end{align}
$$

予測値が複数の場合の予測に関しては「ガウス過程と機械学習」の「公式$3.8$」で取り扱われているので、詳しく確認する際は合わせて参照すると良いと思われる。

ガウス過程と機械学習 (機械学習プロフェッショナルシリーズ)

持橋大地, 大羽成征

2,310円(04/29 09:24時点)

発売日: 2019/03/09

Amazon

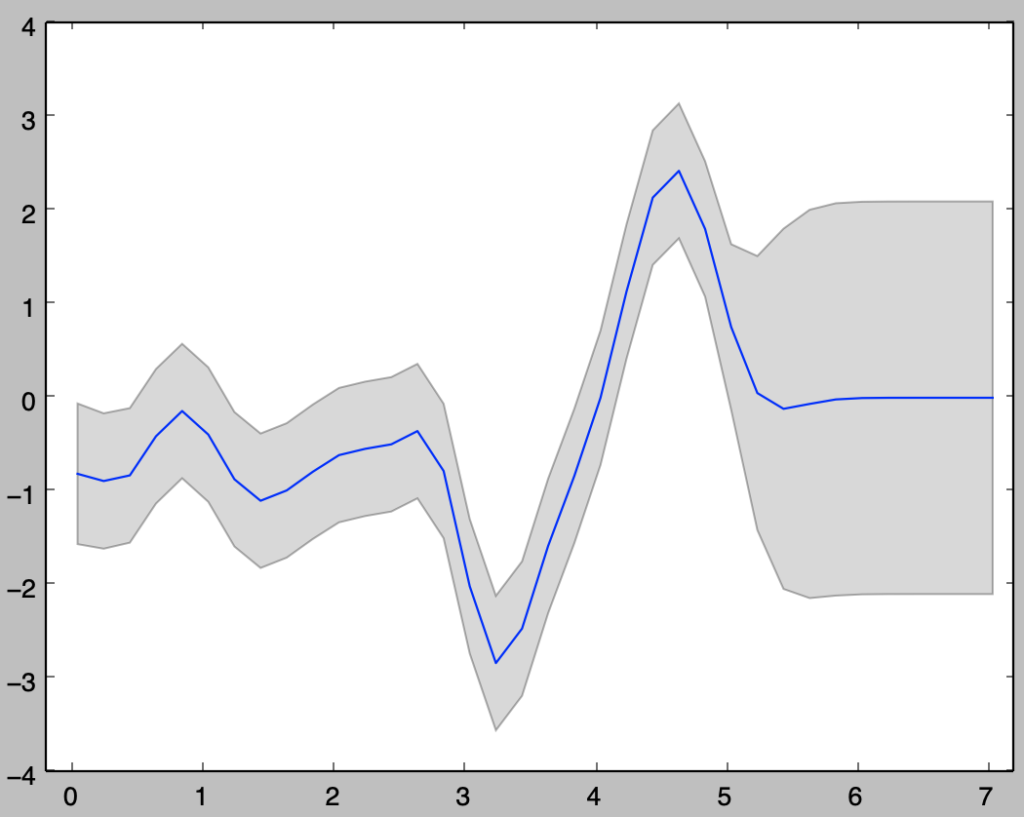
Pythonプログラムを用いたガウス過程回帰の実行

「予測値が複数の場合の予測分布の作成」の内容を元に、以下ガウス過程回帰の計算と図式化を行う。

予測分布

下記を実行することで$2 \sigma$区間の予測分布の作成を行える。

import numpy as np
import matplotlib.pyplot as plt
from scipy import stats

np.random.seed(0)

theta = np.array([1., 10., 0., 0.])

x = np.arange(0.,5.1,0.1)
n = x.shape[0]
sigma2 = 0.02

x_ = np.arange(0.05,7.25,0.2)
n_ = x_.shape[0]

x_all = np.zeros(n+n_)
x_all[:n] = x
x_all[n:] = x_

K = np.zeros([n+n_,n+n_])

for i in range(n+n_):
    for j in range(n+n_):
        K[i,j] = theta[0]*np.exp(-theta[1]*(x_all[i]-x_all[j])**2/2) + theta[2] + theta[3]*x_all[i]*x_all[j]
        if i==j:
            K[i,j] += sigma2*beta

Lamb, U_T = np.linalg.eig(K[:n,:n])
Lamb, U_T = Lamb.real, U_T.real
U = U_T.T

A = np.dot(U_T,np.diag(np.sqrt(Lamb)))
y = np.dot(A,stats.norm.rvs(loc=0,scale=1,size=n))

mu = np.dot(K[n:,:n],np.dot(np.linalg.inv(K[:n,:n]),y))
Sigma = K[n:,n:] - np.dot(K[n:,:n],np.dot(np.linalg.inv(K[:n,:n]),K[:n,n:]))
sigma = np.sqrt(np.diagonal(Sigma))

ly = mu - 2.*sigma
uy = mu + 2.*sigma

plt.plot(x_all[n:],np.dot(K[n:,:n],np.dot(np.linalg.inv(K[:n,:n]),y)))
plt.fill_between(x_all[n:],ly,uy,facecolor="gray",alpha=0.3)
plt.xlim(-0.2,7.2)

plt.show()

・実行結果

ガウス過程回帰の仕組み

同時分布の導出

同時分布の条件付き分布の計算による予測分布の導出

予測値が複数の場合の予測分布の作成

Pythonプログラムを用いたガウス過程回帰の実行

予測分布

関連