ボックス・ミュラー法(Box-Muller’s method)を用いた正規乱数の生成

当記事では一様乱数から正規乱数の生成を行うボックス・ミュラー法(Box-Muller’s method)の原理に関して取り扱いました。ボックス・ミュラー法はガウス積分を行う際と同様の考え方を用いるので、ガウス積分も合わせて抑えておくと良いと思います。
https://www.hello-statisticians.com/explain-terms-cat/gaussian_integral1.html

一様乱数の生成などの他の乱数生成の手法に関しては下記で取りまとめを行いましたので、こちらも合わせてご確認ください。
https://www.hello-statisticians.com/explain-terms-cat/random_sampling1.html

「自然科学の統計学」の$11.3$節を参考に作成を行いました。

自然科学の統計学 (基礎統計学)

3,190円(04/19 13:32時点)

Amazon

ボックス・ミュラー法の概要と導出

乱数生成にあたって用いる式

$$
\large
\begin{align}
X &= \sqrt{-2 \log{U_{1}}} \cdot \cos{(2 \pi U_{2})} \quad (1) \\
Y &= \sqrt{-2 \log{U_{1}}} \cdot \sin{(2 \pi U_{2})} \quad (2)
\end{align}
$$

一様乱数$U_1 \sim \mathrm{Uniform}(0,1), U_2 \sim \mathrm{Uniform}(0,1)$に対し、上記の変換によって得られる$X, Y$は互いに独立に標準正規分布$\mathcal{N}(0,1)$に従う。

よって、$2$つの一様乱数を生成したのちに、$(1)$式、$(2)$式を用いることで標準正規分布$\mathcal{N}(0,1)$に従う乱数を生成できる。この手法をボックス・ミュラー法という。

確率密度関数の変数変換

当項では前項で取り扱ったボックス・ミュラー法を表す$(1)$式$(2)$式が適切な手法であることの確認を行う。以下では$X \sim \mathcal{N}(0,1), Y \sim \mathcal{N}(0,1)$のとき、同時確率分布$f(x,y)$の微小領域の確率$P(x \leq X \leq x+dx,y \leq Y \leq y+dy)$に対し、「ガウス積分」と同様の変数変換を考えることで$(1)$式$(2)$式を導出する。ここで$P(x \leq X \leq x+dx,y \leq Y \leq y+dy)$は確率エレメントということもある。

$X \sim \mathcal{N}(0,1), Y \sim \mathcal{N}(0,1)$より、確率エレメント$P(x \leq X \leq x+dx,y \leq Y \leq y+dy) = f(x,y)dxdy$は下記のように表すことができる。
$$
\large
\begin{align}
f(x,y)dxdy &= f(x)f(y)dxdy \\
&= \frac{1}{\sqrt{2 \pi}} e^{-\frac{x^2}{2}} \cdot \frac{1}{\sqrt{2 \pi}} e^{-\frac{y^2}{2}} dx dy \quad (3)
\end{align}
$$

上記の$(3)$式に対して下記のような変換を行うことを考える。
$$
\large
\begin{align}
x &= r \cos{\theta} \quad (4) \\
y &= r \sin{\theta} \quad (5)
\end{align}
$$

このとき$x,y \to r,\theta$の変換にあたってのヤコビ行列$J$・ヤコビ行列式$|\det J|$は下記のように表される。
$$
\large
\begin{align}
J &= \left(\begin{array}{cc} \frac{\partial x}{\partial r} & \frac{\partial x}{\partial \theta} \\ \frac{\partial y}{\partial r} & \frac{\partial y}{\partial \theta} \end{array} \right) \\
&= \left(\begin{array}{cc} \cos{\theta} & -r \sin{\theta} \\ \sin{\theta} & r \cos{\theta} \end{array} \right) \\
|\det J| &= \left| \begin{array}{cc} \cos{\theta} & -r \sin{\theta} \\ \sin{\theta} & r \cos{\theta} \end{array} \right| \\
&= r \cos^{2}{\theta} + r \sin^{2}{\theta} \\
&= r
\end{align}
$$

よって、$(3)$式は$(4),(5)$式を用いて下記のように変数変換を行うことができる。
$$
\large
\begin{align}
f(x,y)dxdy &= \frac{1}{\sqrt{2 \pi}} e^{-\frac{x^2}{2}} \cdot \frac{1}{\sqrt{2 \pi}} e^{-\frac{y^2}{2}} dx dy \quad (3) \\
&= \frac{1}{2 \pi} e^{-\frac{(r \cos{\theta})^2}{2}} e^{-\frac{(r \sin{\theta})^2}{2}} r dr d \theta \\
&= \frac{1}{2 \pi} e^{-\frac{r^2}{2}} r dr d \theta \quad (6)
\end{align}
$$

上記の$(6)$式に対し、$s=r^2$で変数変換を行うことを考える。このとき下記が成立する。
$$
\large
\begin{align}
\frac{ds}{dr} &= 2r \\
r dr &= \frac{1}{2} ds
\end{align}
$$

$(6)$式は下記のように変数変換を行える。
$$
\large
\begin{align}
\frac{1}{2 \pi} e^{-\frac{r^2}{2}} r dr d \theta &= \frac{1}{2 \pi} e^{-\frac{s}{2}} \frac{1}{2} ds d \theta \\
&= \frac{1}{2 \pi} d \theta \cdot \frac{1}{2} e^{-\frac{s}{2}} ds
\end{align}
$$

ここで上記の$\displaystyle \frac{1}{2 \pi}$は一様分布$\mathrm{Uniform}(0,2 \pi)$の確率密度関数、$\displaystyle \frac{1}{2} e^{-\frac{s}{2}}$は指数分布$\displaystyle \mathrm{Ex} \left( \frac{1}{2} \right)$の確率密度関数に対応する。よって$\displaystyle \Theta \sim \mathrm{Uniform}(0,2 \pi),R^2 \sim \mathrm{Ex} \left( \frac{1}{2} \right)$であるとき、下記の$X,Y$は標準正規分布$\mathcal{N}(0,1)$に従う。
$$
\large
\begin{align}
X &= R \cos{\Theta} \\
Y &= R \sin{\Theta}
\end{align}
$$

ここで上記の乱数$\Theta$を乱数$U_2 \sim \mathrm{Uniform}(0,1)$から得るには$\Theta = 2 \pi U_2$を計算すれば良い。また、乱数$R$を$U_1 \sim \mathrm{Uniform}(0,1)$から得るには$R=\sqrt{-2 \log{U_{1}}}$を計算すればよい。

$R=\sqrt{-2 \log{U_{1}}}$は$\displaystyle R^2 \sim \mathrm{Ex} \left( \frac{1}{2} \right)$であることから逆関数法によって得られる。詳細は次項で取り扱う。

逆関数法と指数分布

逆関数法の原理に関しては上記で詳しく取り扱ったのでここでは省略するが、下記の図を元に考えると良いので図だけ抜粋を行なった。

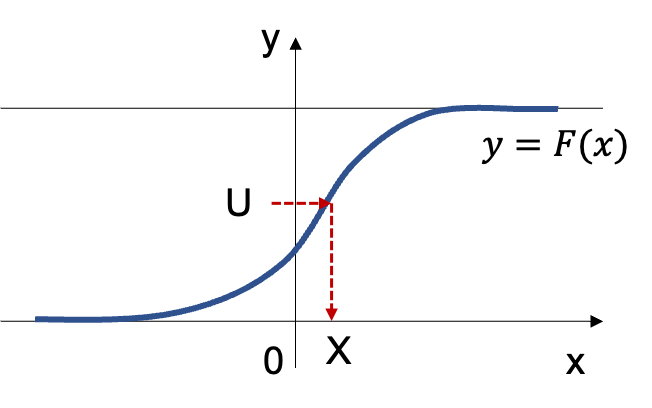
以下、当項では指数分布の累積分布関数$F(x)$を計算し、$R = \sqrt{F^{-1}(U_1)}$に関して計算を行う。パラメータ$\lambda$の指数分布$\mathrm{Ex}(\lambda)$の累積分布関数$F(x)$は下記のように計算できる。
$$
\large
\begin{align}
F(x) &= \int_{0}^{x} \lambda e^{-\lambda t} dt \\
&= \left[ – \frac{\cancel{\lambda}}{\cancel{\lambda}} e^{-\lambda t} \right]_{0}^{x} \\
&= \left[ – e^{-\lambda t} \right]_{0}^{x} \\
&= – e^{-\lambda x} + e^{0} \\
&= 1 – e^{-\lambda x}
\end{align}
$$

よって$u=F(x)$のとき$x=F^{-1}(u)$は下記のように計算できる。
$$
\large
\begin{align}
u &= F(x) \\
u &= 1 – e^{-\lambda x} \\
e^{-\lambda x} &= 1-u \\
-\lambda x &= \log{(1-u)} \\
x &= – \frac{1}{\lambda} \log{(1-u)} \\
F^{-1}(u) &= – \frac{1}{\lambda} \log{(1-u)}
\end{align}
$$

上記の$1-u$は$1$から$0$の一様分布を表すが、$u$で置き換えても$0$から$1$の一様分布に変わるだけなので$1-u$を$u$で置き換えることができる。ここで$\displaystyle \lambda = \frac{1}{2}$を代入すると下記が得られる。
$$
\large
\begin{align}
F^{-1}(u) &= -\frac{1}{\lambda} \log{(1-u)} \\
F^{-1}(u) &= -2 \log{u}
\end{align}
$$

上記より$R = \sqrt{F^{-1}(U_1)} = \sqrt{- 2 \log{U_1}}$によって乱数$R$を生成することができると考えられる。

ボックス・ミュラー法に基づくPythonを用いた正規乱数の生成

標準正規分布$\mathcal{N}(0,1)$に従う乱数の生成

一様乱数は「M系列」などに基づいて作成できるが、以下では簡易化にあたってnp.random.randで代用する。

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(0)

n = 1000
U1, U2 = np.random.rand(n), np.random.rand(n)

X = np.sqrt(-2*np.log(U1)) * np.cos(2*np.pi*U2)
Y = np.sqrt(-2*np.log(U1)) * np.sin(2*np.pi*U2)

samples = np.zeros(n*2)
samples[:n] = X
samples[n:] = Y

plt.hist(samples,bins=50,color="limegreen")
plt.show()

・実行結果

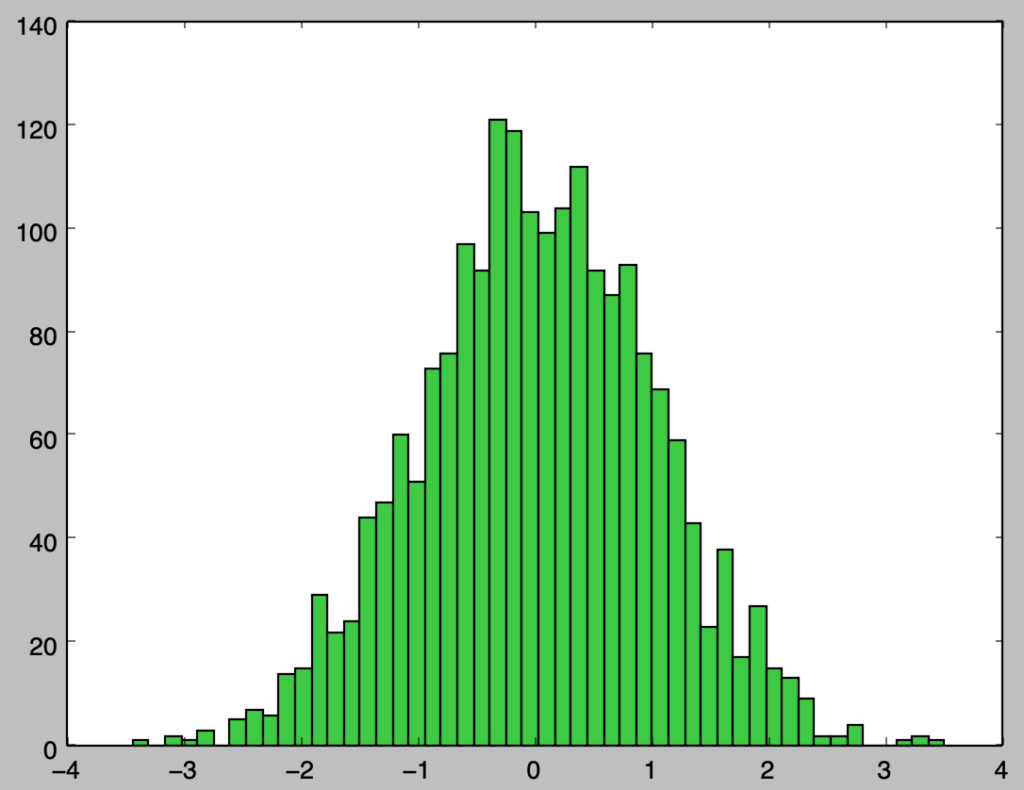
上記では$2000$サンプルの生成を行なったが、$200,000$サンプルまで増やすとどのように変わるかに関しても確認を行う。

np.random.seed(0)

n = 100000
U1, U2 = np.random.rand(n), np.random.rand(n)

X = np.sqrt(-2*np.log(U1)) * np.cos(2*np.pi*U2)
Y = np.sqrt(-2*np.log(U1)) * np.sin(2*np.pi*U2)

samples = np.zeros(n*2)
samples[:n] = X
samples[n:] = Y

plt.hist(samples,bins=50,color="limegreen")
plt.show()

・実行結果

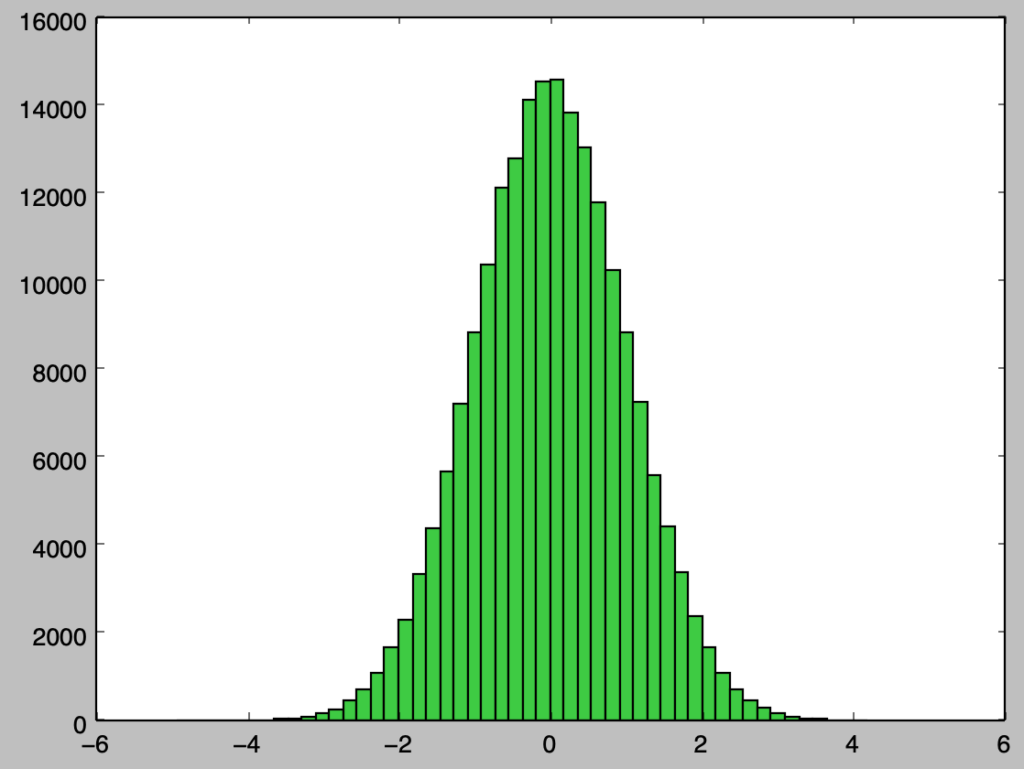
上記のように$200,000$サンプルまで増やすことで正規分布の概形まで得られることが確認できる。

また、下記を実行することで$2$次元ヒストグラムを描くことができる。

np.random.seed(0)

n = 100000
U1, U2 = np.random.rand(n), np.random.rand(n)

X = np.sqrt(-2*np.log(U1)) * np.cos(2*np.pi*U2)
Y = np.sqrt(-2*np.log(U1)) * np.sin(2*np.pi*U2)

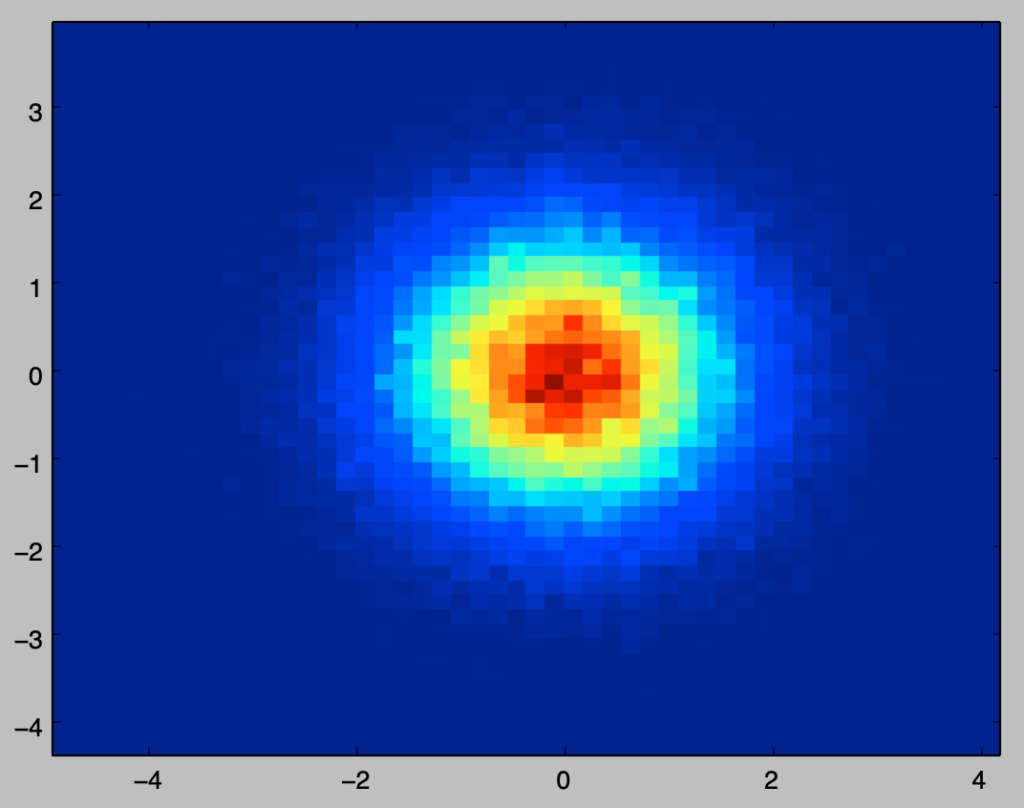
plt.hist2d(X,Y,bins=50)
plt.show()

・実行結果