確率密度関数・確率エレメント・定積分における確率変数の変換にあたっては手順に沿って計算を行えば十分である一方で、公式がわからなくなりがちです。そこで当記事では「ボックス・ミュラー法」の導出を元に難しい点の確認を行なった後になるべく手順に沿って進められるように変数変換の解法に関してフローチャートの形式で取りまとめました。
・参考
ボックス・ミュラー法
ガウス積分
標準演習$100$:確率分布の変数変換
Contents
確率変数の変換はなぜ難しいのか
ボックス・ミュラー法の事例
「ボックス・ミュラー法」の「確率密度関数の変数変換」の事例では「ガウス積分」と同様に、$2$次元の正規分布の変数変換を行うが、まずは計算の概要の確認を行う。
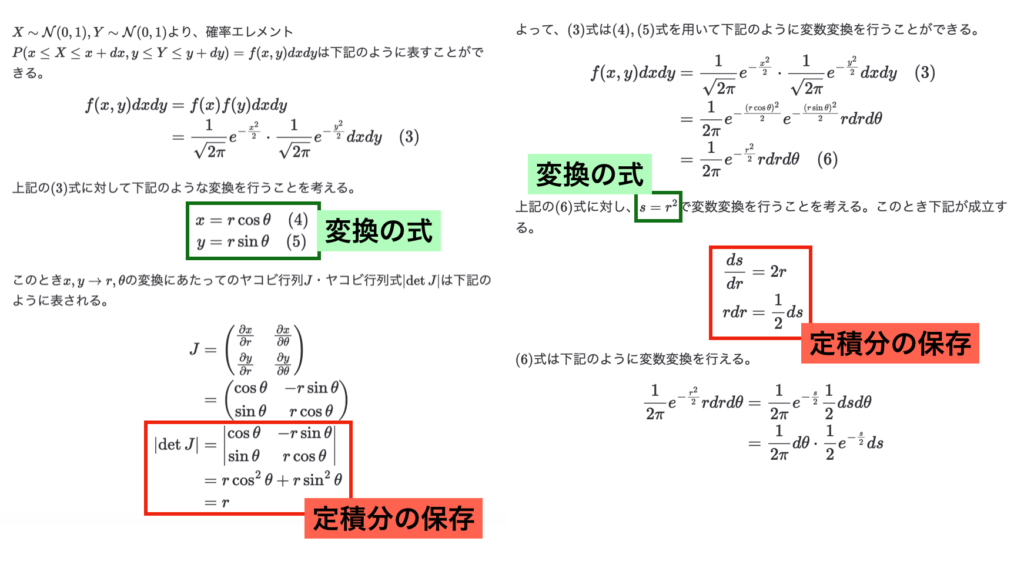
ボックス・ミュラー法では上記のような計算を行うが、変数変換のトピックを一通り抑えてもなかなか再現が難しい。$2$次元の変数変換であり、ヤコビアン(ヤコビ行列式)が出てくるのでシンプルな$1$変数の変換のように簡単な計算にならないというのもあるが、「前半では$x,y \to r,\theta$の変数変換である一方で、後半では$r \to s$の変数変換である」ということでわからなくなりやすいのではないかというのが筆者の仮説である。
もう少し詳細を確認するなら、前半では「$x = r \cos \theta$のように変換前を変換後で表す」のに対し、後半では「$s=r^2$のように変換後を変換前で表す」というところがなかなかわかりにくい。
さらに確率密度関数$f(x)$、確率エレメント$f(x)dx$、定積分$\displaystyle \int_{a}^{b} f(x) dx$のように$dx$があるかないかによって解説に用いられる式の用いられ方が変わる場合があるなど、難しいポイントが多い。
よって次節では当節で確認した内容を元に、確率変数の変数変換の解き方をフローチャートに取りまとめた。
変数変換の解き方フローチャート
フローチャートの概要
フローチャートの作成にあたっては、下記の$3$つに着目を行なった。
$1)$ 確率変数の次元 -> $1$次元と$2$次元以上で分類を行なった
$2)$ 変換対象 -> 確率密度関数$f(x)$、確率エレメント$f(x)dx$、定積分$\displaystyle \int_{a}^{b} f(x) dx$で分類を行なった
$3)$ 変換の式 -> 変換前を$x$、変換後を$y$とするとき、$x=g(y)$の変換式 or $y=g(x)$の変換式で分類を行なった
上記の$3$つの視点を元に、下記のようなフローチャートの作成を行なった。
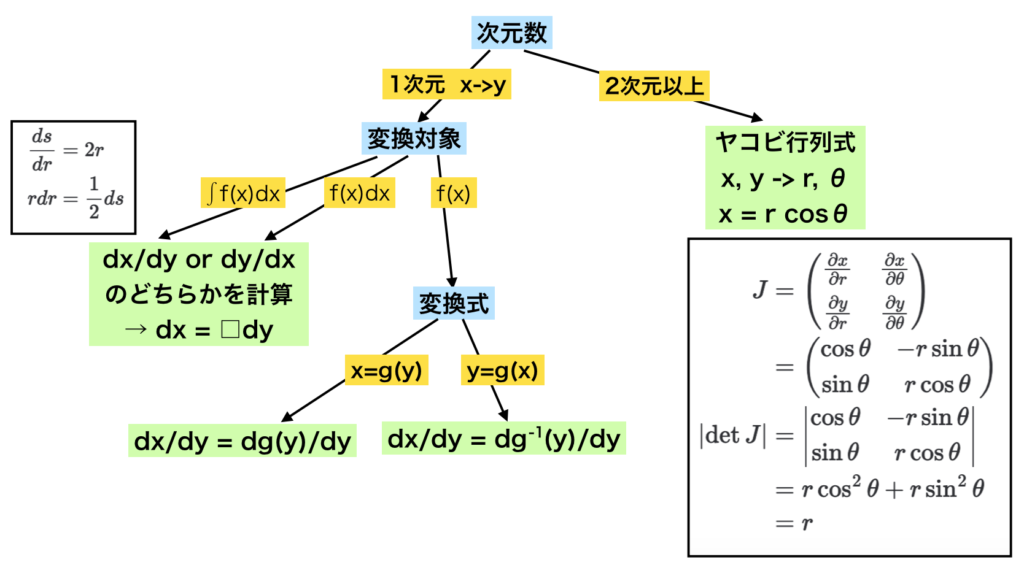
フローチャートの詳細
前項で確認を行なったフローチャートは、$3$つの視点に基づいて作成を行なったので、以下、それぞれの視点に関して詳細の確認を行う。
確率変数の次元
フローチャートではまず確率変数の次元について確認を行なったが、$2$次元以上の場合は基本的にヤコビ行列式を用いるので、ヤコビ行列式の定義に基づいて計算を行えば良い。変換前の変数$x_1,…,x_n$に対して変換後を$y_1,…,y_n$とおくとき、ヤコビ行列式$|\det J|$は下記のように表される。
$$
\large
\begin{align}
J &= \left( \begin{array}{ccc} \frac{\partial x_1}{\partial y_1} & \cdots & \frac{\partial x_1}{\partial y_n} \\ \vdots & \ddots & \vdots \\ \frac{\partial x_n}{\partial y_1} & \cdots & \frac{\partial x_n}{\partial y_n} \end{array} \right) \\
|\det J| &= \left| \begin{array}{ccc} \frac{\partial x_1}{\partial y_1} & \cdots & \frac{\partial x_1}{\partial y_n} \\ \vdots & \ddots & \vdots \\ \frac{\partial x_n}{\partial y_1} & \cdots & \frac{\partial x_n}{\partial y_n} \end{array} \right|
\end{align}
$$
上記では$J$の$(i,j)$成分$(J)_{ij}$に関して$\displaystyle (J)_{ij} = \frac{\partial x_i}{\partial y_j}$のように定義を行なったが、$|\det J| = |\det J^{\mathrm{T}}|$であるので$\displaystyle (J)_{ij} = \frac{\partial x_j}{\partial y_i}$のように定義しても結果は変わらないことも抑えておくとよい。ヤコビ行列式は「変換前と変換後の微小区間の面積の対応」を表すが、詳細は下記で取り扱ったので当項では省略する。
変換対象
変換対象は主に確率密度関数$f(x)$、確率エレメント$f(x)dx$、定積分$\displaystyle \int_{a}^{b} f(x) dx$の$3$パターンあるが、特に着目すべきなのが$dx$がつくかどうかである。$1$次元の変数変換における「定積分の保存」に用いられる微分は$\displaystyle \frac{dx}{dy}$か$\displaystyle \frac{dy}{dx}$のどちらかなので、どちらで計算を行なった場合も$dx = \square dy$を用いて$dx$を$dy$で置き換えればよい。
上記は確率エレメント$f(x)dx$と定積分$\displaystyle \int_{a}^{b} f(x) dx$で共通だが、定積分の計算を行う際は「変数の区間」も「変数の変換」に合わせて変えなければいけないことには注意が必要である。
一方で確率密度関数$f(x)$に関して計算を行う際は$dx$が存在しないので、$x$の確率密度関数$f_1(x)$に対して$y$の確率密度関数$f_2(y)$を$\displaystyle f_2(y)=\left|\frac{dx}{dy}\right|f_1(x)$のように変数変換の公式を用いて計算を行えばよい。
変換の式
変数$x$を$y$に変換する際に、それぞれの確率密度関数を$f_1(x)$、$f_2(y)$のようにおく。このとき、$x=g(y)$の形式の変換の式か$y=g(x)$の形式の変換の式かであることは注意する必要がある。
$x=g(y)$の式の場合はそのまま$\displaystyle \left|\frac{dx}{dy}\right|$を計算し、$\displaystyle f_2(y)=\left|\frac{dg(y)}{dy}\right|f_1(x)$を計算すれば良い。一方で、$y=g(x)$の式の場合は$x=g^{-1}(y)$のように$g$の逆関数を計算したのちに$\displaystyle f_2(y)=\left|\frac{dg^{-1}(y)}{dy}\right|f_1(x)$を計算する必要がある。
このように、$dx$が出てこない場合の変数変換のように公式を用いる場合は、「変換前の変数=変換後の変数の関数の式」で表す必要があることに注意が必要ある。

[…] […]