逆関数法を用いたワイブル分布、ロジスティック分布、コーシー分布に基づく乱数の生成

逆関数法は累積分布関数が値域$(0,1)$かつ単調増加の関数であることに基づいて、区間$(0,1)$で生成する一様乱数を累積分布関数と対応させることで乱数生成を行う手法です。当記事では、ワイブル分布、ロジスティック分布、コーシー分布のそれぞれに対して乱数の生成を行いました。

・参考
逆関数法
自然科学の統計学 第$11$章

自然科学の統計学 (基礎統計学)

3,190円(04/25 14:47時点)

Amazon

逆関数法の概要

上記で詳しく取り扱ったが、下図を元に理解すると良い。

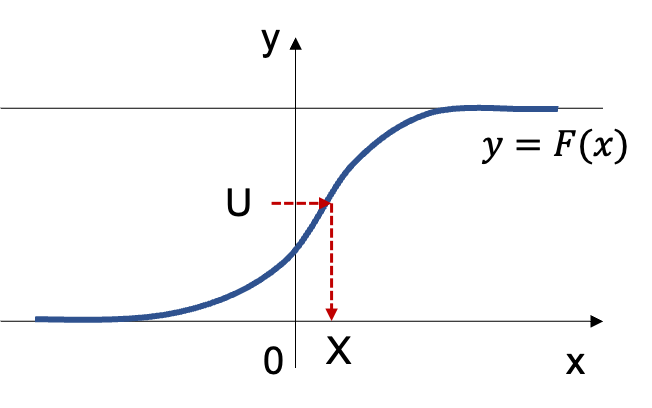
基本的には「累積分布関数」の値域に対して「一様乱数」生成し、定義域に対応させることで乱数を生成すると考えればよい。以下、「逆関数法」で取り扱った「指数分布」の例を元に概要の確認を行う。

指数分布と逆関数法

指数分布の累積分布関数を$F(x)$とおくと「逆関数法：指数分布」より、下記が得られる。
$$
\large
\begin{align}
u &= F(x) = 1 – e^{-\lambda x} \\
x &= F^{-1}(u) = -\frac{1}{\lambda} \log{(1-u)}
\end{align}
$$

一様乱数$U \sim \mathrm{Uniform}(0,1)$を上記に基づいて$\displaystyle X=-\frac{1}{\lambda} \log{(1-U)}$のように変換を行うことで指数分布$\mathrm{Ex}(\lambda)$に基づく乱数が得られる。

また、一様乱数$U \sim \mathrm{Uniform}(0,1)$に対して$1-U$の計算を行うことは$U’ = 1-U \sim \mathrm{Uniform}(0,1)$に基づいて$U’$を用いることと同義であるので、$\displaystyle X=-\frac{1}{\lambda} \log{U}$を用いて乱数の生成を行なっても良い。

ここで$U \neq 1,U’ \neq 0$は必須であるので、乱数の生成にあたっては定義域に注意しておく必要がある。

それぞれの確率分布に基づく乱数の生成

ワイブル分布

式の導出

ワイブル分布の確率密度関数を表す式はいくつかあるが、当項では上記で「統計学実践ワークブック」の$19$章を参考にまとめた下記の数式の表記を用いる。

考にまとめた下記の数式の表記を用いる。
$$
\large
\begin{align}
f(t) = \lambda p (\lambda t)^{p-1} e^{-(\lambda t)^p}, \quad t \geq 0
\end{align}
$$

上記に対し、累積分布関数$\displaystyle F(x) = \int_{0}^{x} f(t) dt$の計算を行う。計算にあたっては$\displaystyle \frac{d}{dt} e^{-(\lambda t)^p}$が下記のように計算できることを元に考えれば良い。
$$
\large
\begin{align}
\frac{d}{dt} e^{-(\lambda t)^p} &= e^{-(\lambda t)^p} \frac{d}{dt} (-(\lambda t)^p) \\
&= e^{-(\lambda t)^p} (-p \lambda^{p} t^{p-1}) \\
&= – \lambda p (\lambda t)^{p-1} e^{-(\lambda t)^p}
\end{align}
$$

よって、$\displaystyle F(x) = \int_{0}^{x} f(t) dt$は下記のように計算できる。
$$
\large
\begin{align}
F(x) &= \int_{0}^{x} f(t) dt \\
&= \left[ -e^{-(\lambda t)^p} \right]_{0}^{x} \\
&= 1 – e^{-(\lambda x)^p}
\end{align}
$$

上記に対し$u=F(x)$とおくと、$x=F^{-1}(u)$は下記のように導出できる。
$$
\large
\begin{align}
u &= F(x) \\
&= 1 – e^{-(\lambda x)^p} \\
e^{-(\lambda x)^p} &= 1-u \\
-(\lambda x)^p &= \log{(1-u)} \\
\lambda x &= (-\log{(1-u)})^{\frac{1}{p}} \\
x &= \frac{(-\log{(1-u)})^{\frac{1}{p}}}{\lambda} = F^{-1}(u)
\end{align}
$$

Pythonを用いた乱数生成

まずはワイブル分布の確率密度関数の確認を行う。下記を実行することでワイブル分布の確率密度関数のグラフを作成することができる。

import numpy as np
import matplotlib.pyplot as plt

x = np.arange(0.,2.01,0.01)

lamb = np.array([1., 1., 2., 2., 5.])
p = np.array([5., 10., 5., 10., 5.])

for i in range(lamb.shape[0]):
    y = lamb[i]*p[i]*(lamb[i]*x)**(p[i]-1) * np.e**(-(lamb[i]*x)**p[i])
    plt.plot(x,y,label="lambda: {:.0f}, p: {:.0f}".format(lamb[i],p[i]))

plt.legend()
plt.show()

・実行結果

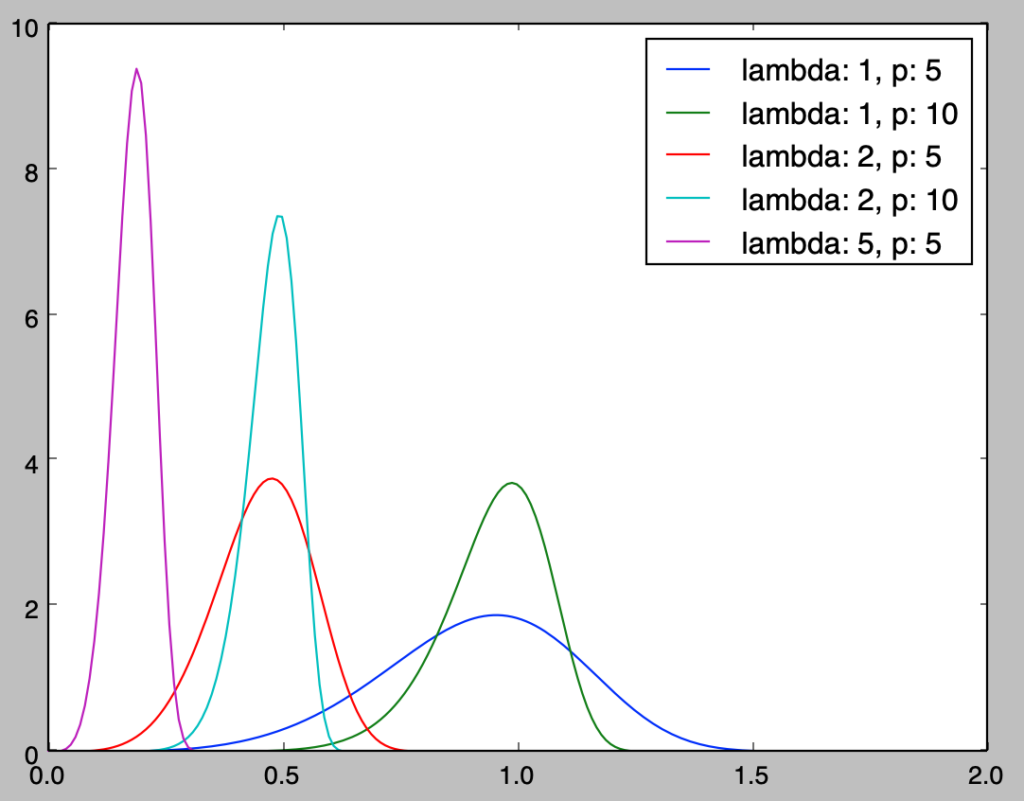
上記の緑のグラフなどを確認することにより、$x$の増加に伴いハザード関数$h(x)$が増大するIFRであることも確認できる。当記事の主題ではないので詳しくは省略するが、「ワイブル分布の瞬間故障率$h(t)$の計算」で取り扱ったようにワイブル分布はハザード関数の増減を調整できる分布である。

上記の緑の設定である$\lambda = 1, p = 10$に対して、以下では$\displaystyle X = F^{-1}(U) = \frac{(-\log{(1-U)})^{\frac{1}{p}}}{\lambda}$を用いて乱数生成を行う。

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(0)

lamb, p = 1., 10.
x = np.arange(0.,2.01,0.01)
y = lamb*p*(lamb*x)**(p-1) * np.e**(-(lamb*x)**p)

U = np.random.rand(1000)
X = (-np.log(1-U))**(1/p)/lamb

plt.subplot(211)
plt.plot(x,y,color="green")
plt.subplot(212)
plt.hist(X,bins=50,color="limegreen")
plt.xlim([0.,2.])
plt.show()

・実行結果

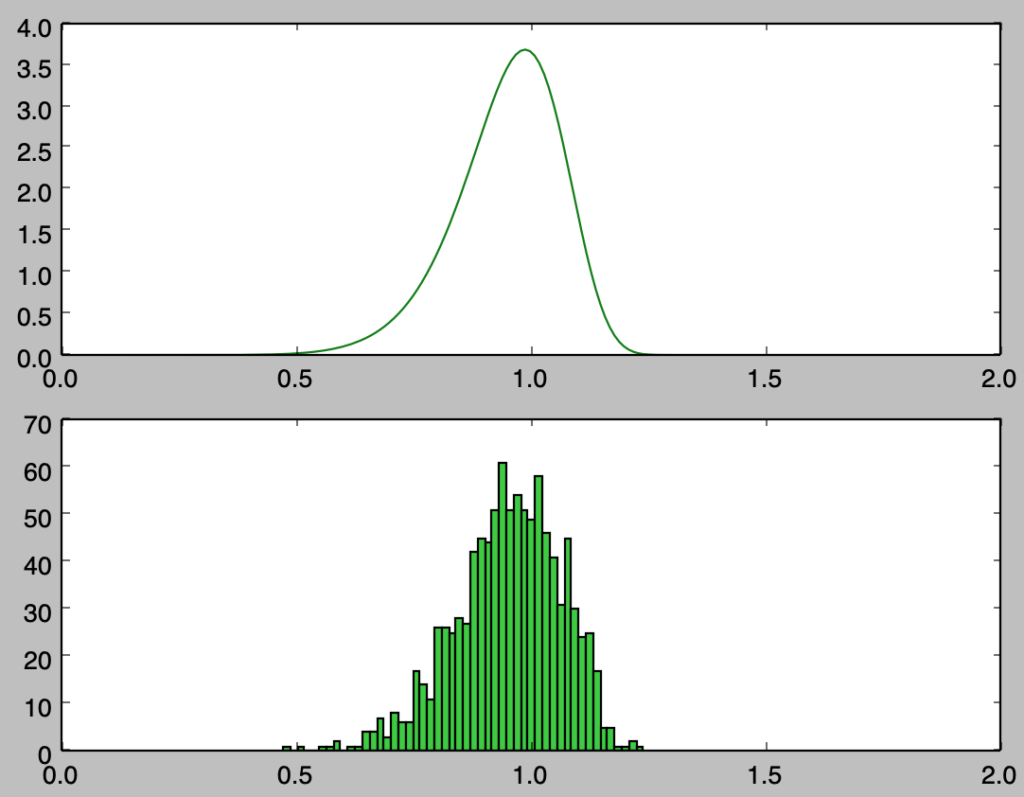
上記は$1,000$サンプルのヒストグラムの描画を行なったが、概ね確率密度関数に沿って乱数が得られたことが確認できる。また、サンプル数を増やした際の挙動を確認するにあたって以下では$100,000$サンプルでヒストグラムの描画を行なった。

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(0)

lamb, p = 1., 10.
x = np.arange(0.,2.01,0.01)
y = lamb*p*(lamb*x)**(p-1) * np.e**(-(lamb*x)**p)

U = np.random.rand(100000)
X = (-np.log(1-U))**(1/p)/lamb

plt.subplot(211)
plt.plot(x,y,color="green")
plt.subplot(212)
plt.hist(X,bins=50,color="limegreen")
plt.xlim([0.,2.])
plt.show()

・実行結果

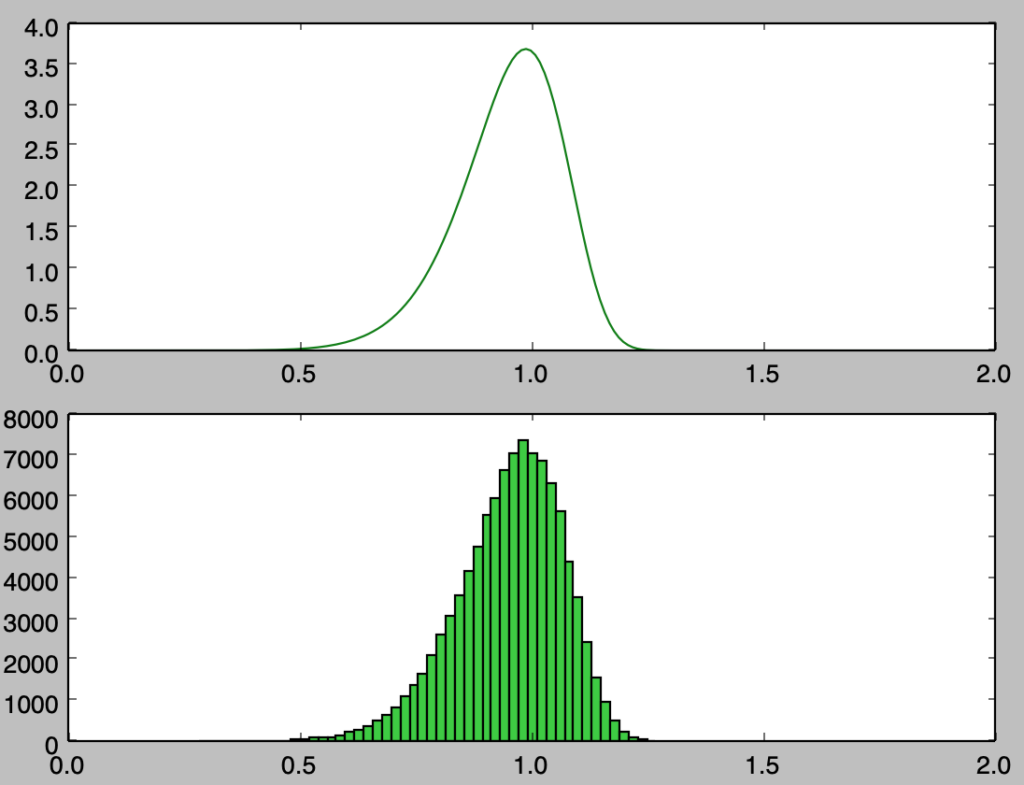
ロジスティック分布

式の導出

$$
\large
\begin{align}
f(x) = \frac{\exp(-x)}{(1+\exp(-x))^2}
\end{align}
$$

上記のような確率密度関数$f(x)$を持つ分布をロジスティック分布という。累積分布関数の$F(x)$はロジスティック回帰などに用いられることで取り扱われることが多い一方でロジスティック分布が取り扱われることは少ないように思われるが、「統計検定$1$級対応テキスト」の$2.2.9$節などではロジスティック分布が取り扱われており当項の作成にあたって主に参照した。累積分布関数の$F(x)$は確率密度関数$f(x)$の積分を考えることで、下記のように導出できる。
$$
\large
\begin{align}
F(x) &= \int_{-\infty}^{x} f(t) dt \\
&= \int_{-\infty}^{x} \frac{\exp(-t)}{(1+\exp(-t))^2} dt \\
&= \int_{-\infty}^{x} \frac{-(1+\exp(-t))’}{(1+\exp(-t))^2} dt \\
&= \int_{-\infty}^{x} \left( \frac{1}{1+\exp(-t)} \right)’ dt \\
&= \left[ \frac{1}{1+\exp(-t)} \right]_{-\infty}^{x} \\
&= \frac{1}{1+\exp(-x)} \quad (1)
\end{align}
$$

上記はシグモイド関数という名称でも知られ、ニューラルネットワークなどにも応用される関数であるので重要である。

日本統計学会公式認定 統計検定1級対応 統計学

二宮嘉行, 大西俊郎, 小林 景, 椎名 洋, 笛田 薫

7,000円(04/25 15:58時点)

Amazon

以下、$(1)$式を$u=F(x)$とおくときの逆関数$u=F^{-1}(x)$の導出を行う。
$$
\large
\begin{align}
u &= F(x) \\
&= \frac{1}{1+\exp(-x)} \\
u(1+\exp(-x)) &= 1 \\
u \exp(-x) &= 1-u \\
\exp(-x) &= \frac{1-u}{u} \\
\exp(x) &= \frac{u}{1-u} \\
x &= \log{\frac{u}{1-u}} = F^{-1}(u)
\end{align}
$$

Pythonを用いた乱数生成

まずはロジスティック分布の確率密度関数の確認を行う。下記を実行することでロジスティック分布の確率密度関数のグラフを作成することができる。

import numpy as np
import matplotlib.pyplot as plt

x = np.arange(-5.,5.02,0.02)
y = np.e**(-x)/(1.+np.e**(-x))**2

plt.plot(x,y)
plt.xlim([-5.,5.])
plt.show()

・実行結果

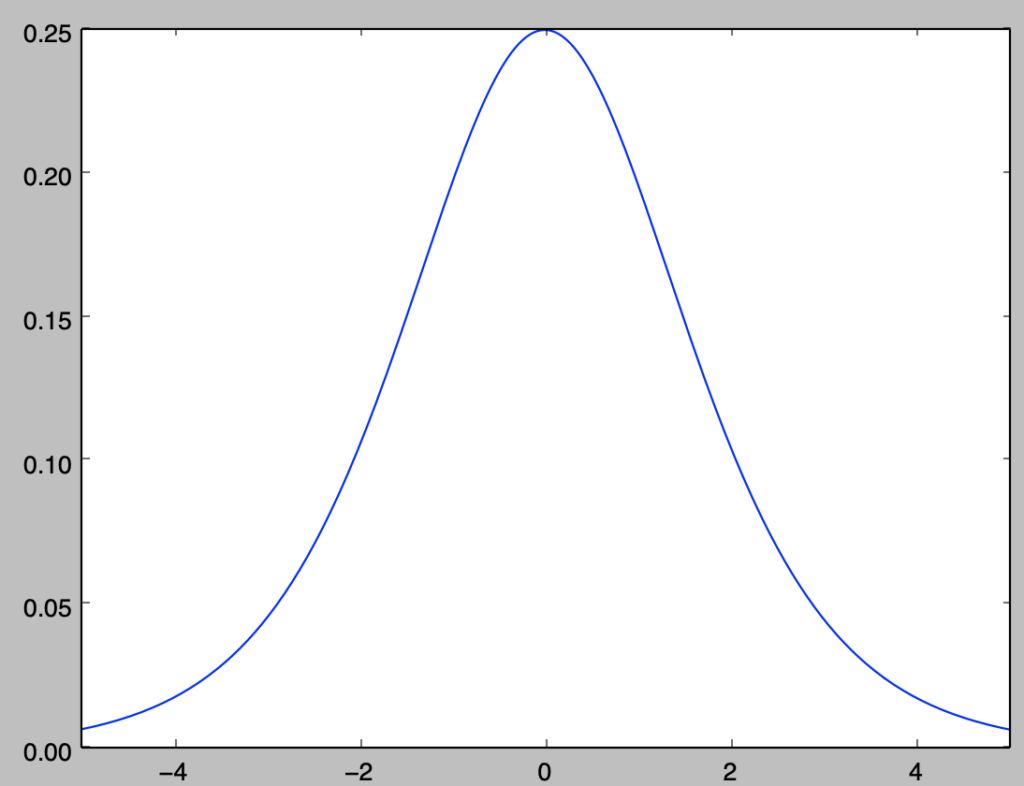
上記は正規分布に近いので、ロジスティック回帰がプロビット回帰の代用で用いられることが多い。以下、$\displaystyle X = F^{-1}(U) = \log{\frac{U}{1-U}}$を用いて乱数生成を行う。

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(0)

x = np.arange(-5.,5.02,0.02)
y = np.e**(-x)/(1.+np.e**(-x))**2

U = np.random.rand(1000)
X = np.log(U/(1-U))

plt.subplot(211)
plt.plot(x,y,color="green")
plt.subplot(212)
plt.hist(X,bins=50,color="limegreen")
plt.xlim([-5.,5.])
plt.show()

・実行結果

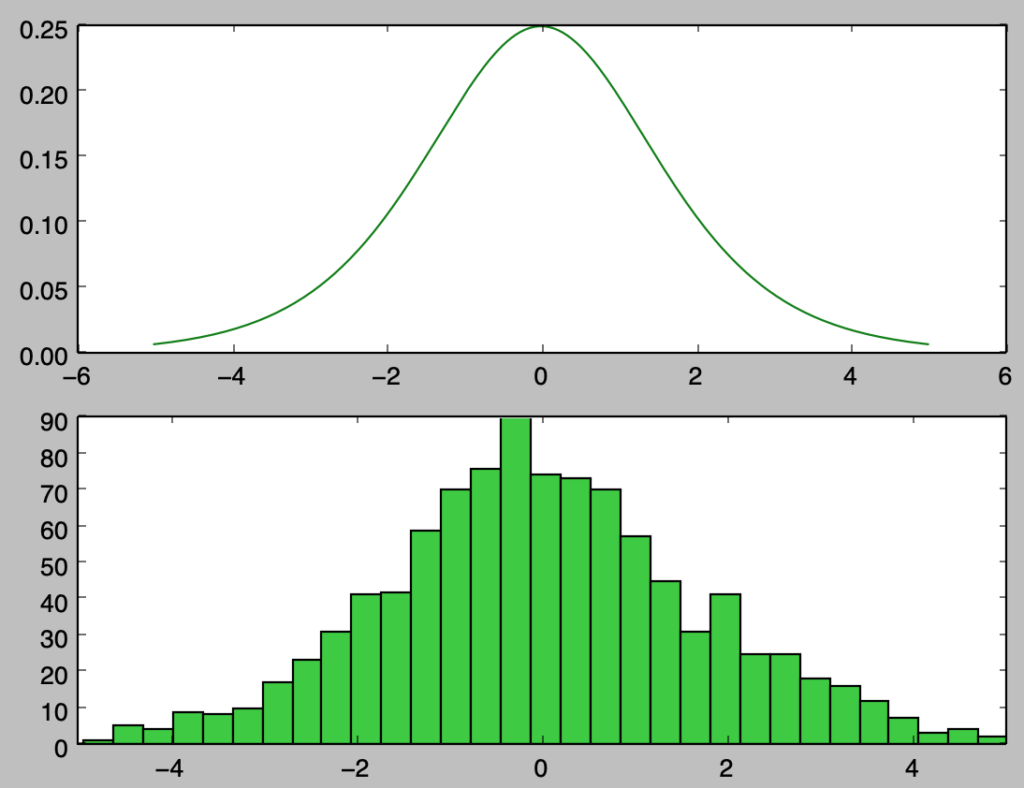
上記は$1,000$サンプルのヒストグラムの描画を行なったが、概ね確率密度関数に沿って乱数が得られたことが確認できる。また、サンプル数を増やした際の挙動を確認するにあたって以下では$100,000$サンプルでヒストグラムの描画を行なった。

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(0)

x = np.arange(-5.,5.02,0.02)
y = np.e**(-x)/(1.+np.e**(-x))**2

U = np.random.rand(100000)
X = np.log(U/(1-U))

plt.subplot(211)
plt.plot(x,y,color="green")
plt.subplot(212)
plt.hist(X,bins=50,color="limegreen")
plt.xlim([-5.,5.])
plt.show()

・実行結果

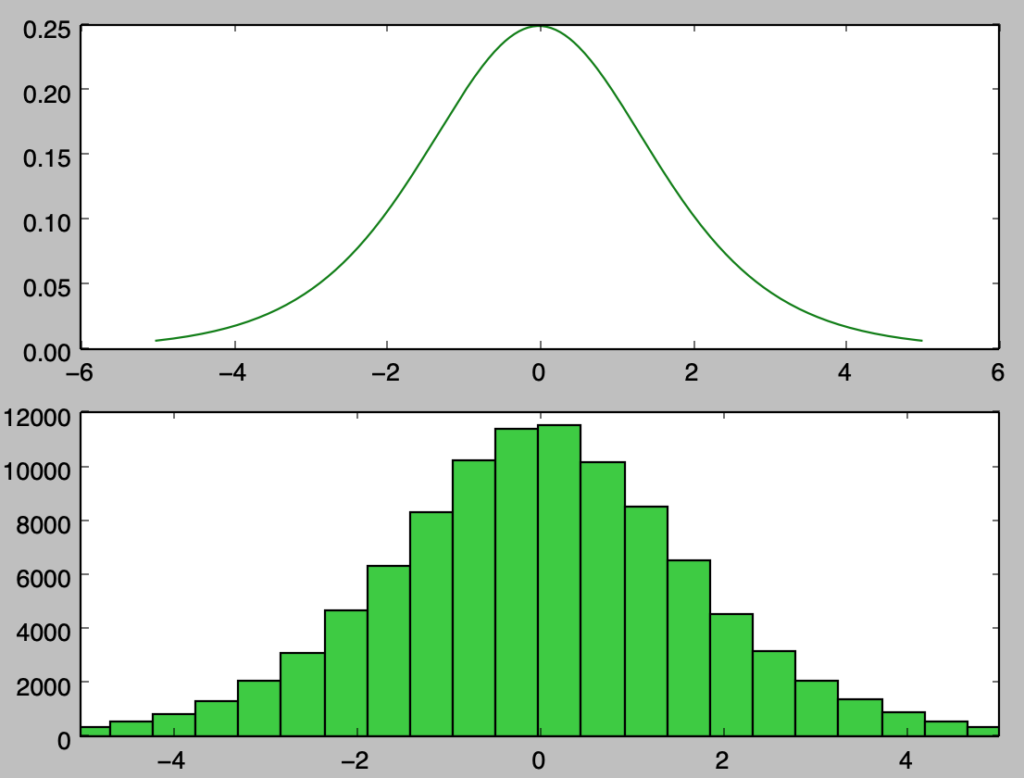
実行にあたって、plt.histの集計にあたってbins=50を設定した一方で、図ごとに数に差があるのは最大値と最小値が大きいと区間$[-5,5]$内の区切りが少なくなることに起因すると理解すると良い。

コーシー分布

式の導出

自然科学の統計学 (基礎統計学)

3,190円(04/25 14:47時点)

Amazon

「自然科学の統計学」の$2.1$節ではコーシー分布の確率密度関数$f(t)$は下記のように表される。
$$
\large
\begin{align}
f(t) = \frac{1}{\pi} \cdot \frac{1}{1+t^2}
\end{align}
$$

上記に対し、累積分布関数$\displaystyle F(x) = \int_{-\infty}^{x} f(t) dt$の計算を行うことを考える。$F(x)$は下記のように表せる。
$$
\large
\begin{align}
F(x) &= \int_{-\infty}^{x} f(t) dt \\
&= \int_{-\infty}^{x} \frac{1}{\pi} \cdot \frac{1}{1+t^2} dt \\
&= \frac{1}{\pi} \int_{-\infty}^{x} \frac{1}{1+t^2} dt \quad (2)
\end{align}
$$

上記に対し、$t=\tan{\theta}$で置換積分を行うことを考える。ここで$-\infty \leq t \leq x$には$\displaystyle -\frac{\pi}{2} \leq \theta \leq \tan^{-1}(x)$が対応し、$dt$と$d \theta$に関しては下記が成立する。
$$
\large
\begin{align}
\frac{dt}{d \theta} &= \frac{d}{d \theta} \tan{\theta} \\
&= \left( \frac{\sin{\theta}}{\cos{\theta}} \right)’ \\
&= \frac{(\sin{\theta})’\cos{\theta}-\sin{\theta}(\cos{\theta})’}{\cos^2{\theta}} \\
&= \frac{\cos^2{\theta}+\sin^2{\theta}}{\cos^2{\theta}} \\
&= \frac{1}{\cos^2{\theta}}
\end{align}
$$

また、$\displaystyle \frac{1}{1+t^2}$に$t=\tan{\theta}$を代入すると下記のように変形できる。
$$
\large
\begin{align}
\frac{1}{1+t^2} &= \frac{1}{1+\tan^{2}{\theta}} \\
&= \frac{1}{\displaystyle 1 + \frac{\sin^{2}{\theta}}{\cos^{2}{\theta}}} \\
&= \frac{\cos^{2}{\theta}}{\cos^{2}{\theta} + \sin^{2}{\theta}} \\
&= \frac{\cos^{2}{\theta}}{1} \\
&= \cos^{2}{\theta}
\end{align}
$$

ここまでの内容を元に、$(2)$式は下記のように変数の変換を行える。
$$
\large
\begin{align}
F(x) &= \frac{1}{\pi} \int_{-\infty}^{x} \frac{1}{1+t^2} dt \quad (2) \\
&= \frac{1}{\pi} \int_{-\frac{\pi}{2}}^{\tan^{-1}(x)} \frac{1}{1+\tan^2{\theta}} \frac{1}{\cos^2{\theta}} d \theta \\
&= \frac{1}{\pi} \int_{-\frac{\pi}{2}}^{\tan^{-1}(x)} \frac{\cancel{\cos^2{\theta}}}{\cancel{\cos^2{\theta}}} d \theta \\
&= \frac{1}{\pi} \left[ \theta \right]_{-\frac{\pi}{2}}^{\tan^{-1}{(x)}} \\
&= \frac{1}{\pi}\tan^{-1}{(x)} + \frac{\cancel{\pi}}{2 \cancel{\pi}} \\
&= \frac{1}{\pi}\tan^{-1}{(x)} + \frac{1}{2}
\end{align}
$$

上記に対し$u=F(x)$とおくと、$x=F^{-1}(u)$は下記のように導出できる。
$$
\large
\begin{align}
u &= F(x) \\
&= \frac{1}{\pi}\tan^{-1}{(x)} + \frac{1}{2} \\
\frac{1}{\pi}\tan^{-1}{(x)} &= u – \frac{1}{2} \\
\tan^{-1}{(x)} &= \pi \left( u – \frac{1}{2} \right) \\
x &= \tan \left[ \left( u – \frac{1}{2} \right) \pi \right] = F^{-1}(u)
\end{align}
$$

・参考
自由度$\nu=1$の$t$分布：コーシー分布

Pythonを用いた乱数生成

まずはコーシー分布の確率密度関数の確認を行う。下記を実行することでコーシー分布の確率密度関数のグラフを作成することができる。

import numpy as np
import matplotlib.pyplot as plt
from scipy import stats

x = np.arange(-3.,3.01,0.01)
y = 1./(np.pi*(1+x**2))
y_norm = stats.norm.pdf(x)

plt.plot(x,y,label="Cauchy Dist")
plt.plot(x,y_norm,label="Norm Dist")

plt.legend()
plt.show()

・実行結果

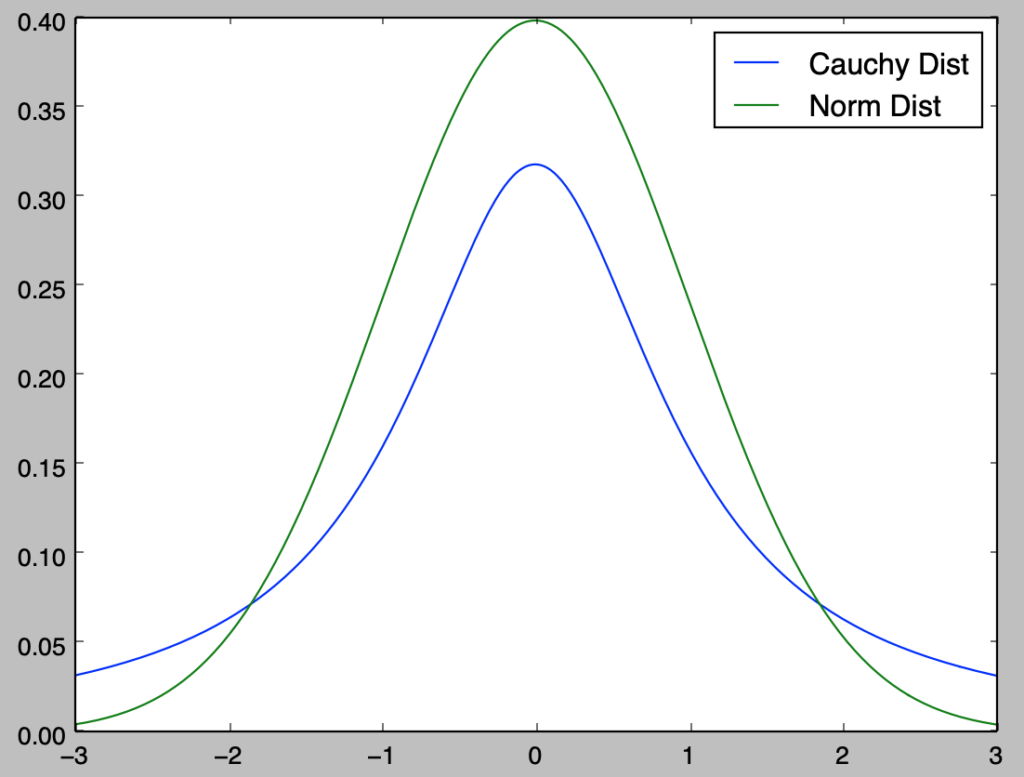
上記ではコーシー分布と正規分布の確率密度関数の描画を行なった。両者は概ね同様の形状である一方で、中心から遠い点でもコーシー分布はなかなか$0$に収束せず、このことからコーシー分布は平均などのモーメントが存在しない分布の例に用いられることが多い。

以下では$\displaystyle X = F^{-1}(U) = \tan \left[ \left( U – \frac{1}{2} \right) \pi \right]$を用いて乱数生成を行う。

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(0)

x = np.arange(-3.,3.01,0.01)
y = 1./(np.pi*(1+x**2))

U = np.random.rand(1000)
X = np.tan((U-1./2.)*np.pi)

plt.subplot(211)
plt.plot(x,y,color="green")
plt.subplot(212)
plt.hist(X,bins=10000,color="limegreen")
plt.xlim([-3.,3.])
plt.show()

・実行結果

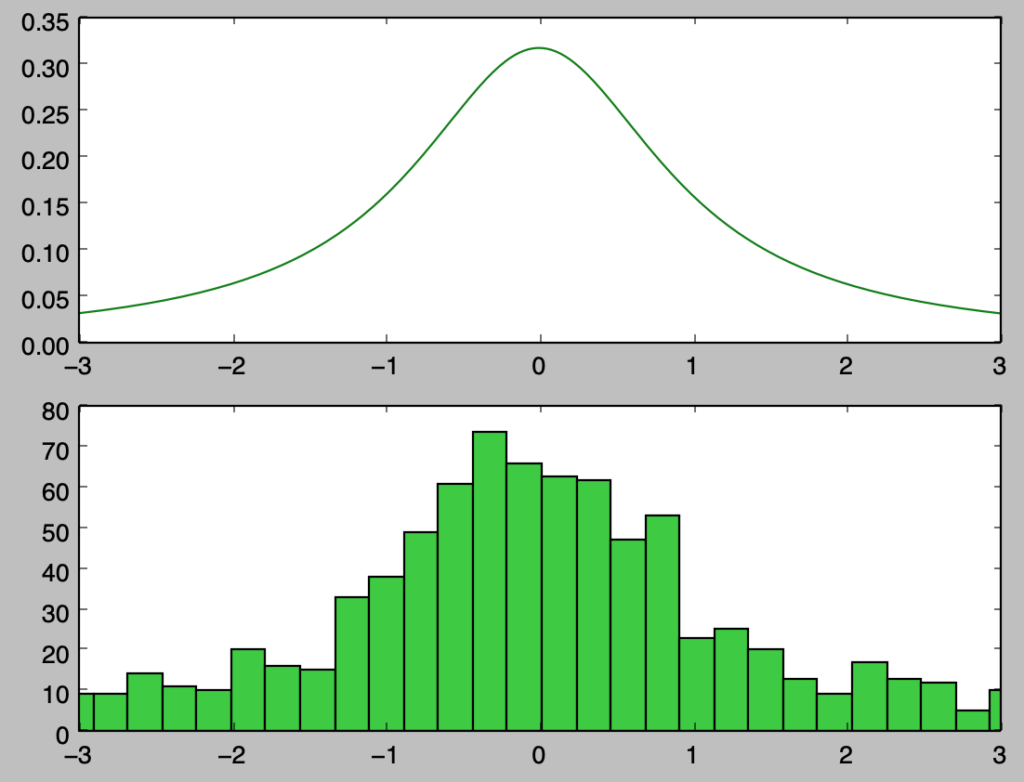
bins=10000に設定したので実行にあたっては注意が必要

上記の実行にあたって、コーシー分布では最小値・最大値の絶対値が大きくなることからbins=10000で設定を行なった。計算量が多いので、実行にあたっては止まる場合があることに注意が必要である。

以下、サンプル数を$100,000$に増やすのではなく、コーシー分布と正規分布の乱数の最大値・最小値をそれぞれ確認を行う。

正規分布の乱数生成と最大値、最小値

from scipy import stats

np.random.seed(0)

X1 = stats.norm.rvs(size=1000)
X2 = stats.norm.rvs(size=10000000)

print("min X1: {:.2f}, max X1: {:.2f}".format(min(X1), max(X1)))
print("min X2: {:.2f}, max X2: {:.2f}".format(min(X2), max(X2)))

・実行結果

min X1: -2.88, max X1: 3.73
min X2: -5.44, max X2: 5.22

コーシー分布の乱数生成と最大値、最小値

import numpy as np

np.random.seed(0)

U1 = np.random.rand(1000)
U2 = np.random.rand(10000000)

X1 = np.tan((U1-1./2.)*np.pi)
X2 = np.tan((U2-1./2.)*np.pi)

print("min X1: {:.2f}, max X1: {:.2f}".format(min(X1), max(X1)))
print("min X2: {:.2f}, max X2: {:.2f}".format(min(X2), max(X2)))

・実行結果

min X1: -583.02, max X1: 1662.87
min X2: -12647485.80, max X2: 2326381.31

自然科学の統計学 (基礎統計学)

3,190円(04/25 14:47時点)

Amazon