逆関数法(inverse transformation method) -確率分布に従う乱数生成-

確率モデルに基づいたシミュレーションを行う際に、確率モデルに現れる確率分布に従う乱数を生成することが必要になります。逆関数法(inverse transformation method)を使うことで、一様乱数から任意の確率分布に従う乱数を生成することができます。
ここでは、この逆関数法の解説と乱数生成の例を紹介します。

逆関数法

発生させたい乱数を$X$、$X$の密度関数を$f(x)$とする。また、$f(x)$の累積分布関数を$F(x)$として、$F(x)$は連続であるとする。$F(x)$は密度関数の定義から、範囲は$[0, 1]$となる。

分布関数$F(x)$の逆関数$F^{-1}(u)$が求められる場合に以下の手順で乱数$X$を生成する方法を逆関数法(inverse transformation method)と呼ぶ。

1. 一様乱数$u$を生成（$u \sim \mathrm{U}(0, 1)$）
2. $x = F^{-1}(u)$として乱数$x$を得る

逆関数法による乱数生成については以下の図をイメージしてもらえれば容易に理解できます。

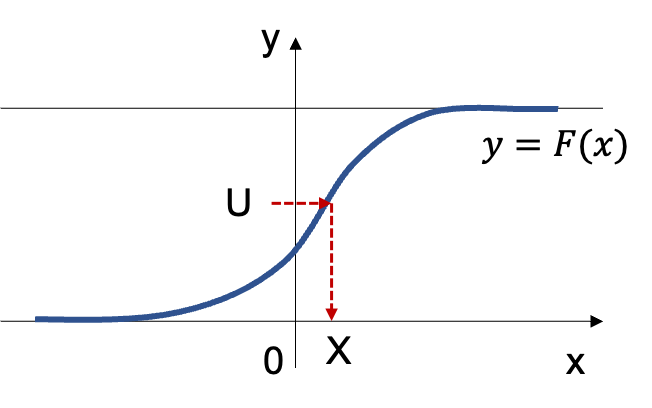
逆関数法の証明

逆関数による変数$F^{-1}(U)=X$が、累積分布関数が$F(x)$の確率密度関数に従うことを示します。

$X$の分布関数は$P(X \leq x)$であり、$X=F^{-1}(U)$であるため以下の等式が成り立ちます。

$$
P(X \leq x) = P(F^{-1}(U) \leq x)
$$

関数$F(\cdot)$を戻すと

$$
P(F^{-1}(U) \leq x) = P(U \leq F(x))
$$

となります。ここで、Uは一様分布に従うとすると、$P(U \leq u) = u$となります。この関係を利用することで、

$$
P(U \leq F(x)) = F(x)
$$

となります。
よって、$X$の累積分布関数は$F(x)$となることがわかりました。

乱数生成の例

逆関数法を利用して実際に乱数を生成してみます。

指数分布

初めに、単純な例として、指数分布に従う乱数生成を試してみます。

逆関数の導出

指数分布は以下の式で定義されています。

$$
f(x) = \lambda \exp(-\lambda x)
$$

指数分布の累積分布関数は範囲xまで積分することで導出できます。

$$
\begin{align}
F(x) &= \int^x_0 \lambda \exp(-\lambda x) dx \\
&= \left[ \lambda \left( -\frac{1}{\lambda} \right) \exp(-\lambda x) \right]^x_0 \\
&= 1 – \exp(-\lambda x)
\end{align}
$$

逆関数$F^{-1}(U)$は以下の通りです。

$$
\begin{align}
U &= 1 – \exp(-\lambda x) \\
\exp(-\lambda x) &= 1 – U \\
x &= – \frac{1}{\lambda} \log(1-U)
\end{align}
$$

シミュレーション

Pythonを利用したシミュレーション結果を添付します。

from scipy import stats

mu = 0.5
ran = stats.uniform.rvs(size=10000)
sample_exp_f = -1./mu * np.log( 1.0 - ran )

fig = plt.figure(figsize=(6,3))
ax = fig.subplots(1,1)
bins = np.linspace(0, 17, 50)
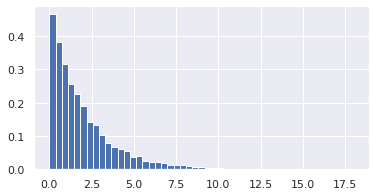
_ = ax.hist(sample_exp_f, bins=bins, density=True)

この結果は以下のようになります。これは、上記コードの通り、生成した乱数のヒストグラムです。つまり指数分布の密度関数を近似しています。

切断指数分布

指数分布と関連してもう少し複雑な例として、切断指数分布に従う乱数を逆関数法で生成してみます。

切断指数分布の確率密度関数

指数分布の値域は$[0, \infty)$ですが、切断指数分布は$[0, T]$であり、指数分布がTまでで切断されたものとなっています。関数の形としては指数分布と同様ですが、切断されているために正規化定数が異なります。密度関数の定義として積分して1となることは変わらないですので。

そこで初めに、正規化定数を導出して切断指数分布の密度関数を確認します。

$$
\begin{align}
\int^T_0 \exp(-\lambda x)dx &= \left[ -\frac{1}{\lambda} \exp(-\lambda x) \right]^T_0 \\
&= \frac{1 – \exp(-\lambda T)}{\lambda}
\end{align}
$$

よって確率密度関数$f(x)$は以下のようになります。

$$
f(x) = \frac{\lambda}{1 – \exp(-\lambda T)} \exp(-\lambda x)
$$

逆関数の導出

指数分布の場合と同様にして、累積分布関数を導出して、そこから逆関数を導出します。

累積分布関数は以下の通りです。

$$
\begin{align}
F(x) &= \int^x_0 \frac{\lambda}{1 – \exp(-\lambda T)} \exp(-\lambda x) dx \\
&= \frac{\lambda}{1 – \exp(-\lambda T)} \left\{ 1 – \exp(-\lambda x) \right\}
\end{align}
$$

逆関数は以下の通りとなります。

$$
\begin{align}
U &= \frac{\lambda}{1 – \exp(-\lambda T)} \left\{ 1 – \exp(-\lambda x) \right\} \\
x &= -\frac{1}{\lambda} \log\left\{ 1 – \left(1 – \exp(-\lambda T)\right)U \right\}
\end{align}
$$

シミュレーション

Pythonを利用したシミュレーション結果を示します。

from scipy import stats

T = 3
mu = 0.5
ran = stats.uniform.rvs(size=10000)
samples_t_exp = -1.0/mu * np.log( 1.0 - ran*(1.-np.exp(-1*mu*(T))) )

fig = plt.figure(figsize=(6,3))
ax = fig.subplots(1,1)
bins = np.linspace(0, 17, 50)
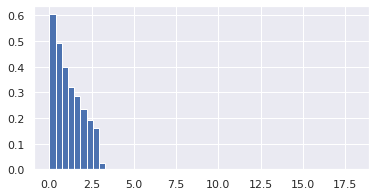
_ = ax.hist(samples_t_exp, bins=bins, density=True)

この結果は以下のようになります。

参考資料

• 矢島ら, 自然科学の統計学, 1992, 東京大学出版会

自然科学の統計学 (基礎統計学)

3,190円(09/28 16:36時点)

Amazon