ソフトマックス関数に基づく確率分布に基づいてサンプリングを行うにあたって、$\exp(x)$がオーバーフローを起こす場合があります。当記事ではこのような際に有用なガンベル最大トリック(Gumbel-max trick)の仕組みとPythonプログラムの作成を取り扱いました。
当記事の作成にあたっては「深層学習による自然言語処理」の$7.3.2$項の「ガンベル最大トリック」を参考にしました。
・用語/公式解説
https://www.hello-statisticians.com/explain-terms
Contents
ガンベル最大トリックのアルゴリズム
ガンベル分布
位置パラメータ$0$、尺度パラメータ$1$のガンベル分布の累積分布関数を$F(x)$、確率密度関数を$f(x)$とおくと、それぞれ下記のように表すことができる。
$$
\large
\begin{align}
F(x) &= \exp{[-\exp{(-x)}]} \\
f(x) &= \frac{d}{dx}F(x) = \exp{[-\exp{(-x)}]} \times -\exp{(-x)} \times (-1) \\
&= \exp{(-x)} \exp{[-\exp{(-x)}]} = \exp{(-x)} F(x)
\end{align}
$$
累積分布関数$F(x)$のグラフは下記のように描くことができる。
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_theme()
x = np.arange(-5., 5.01, 0.01)
F_x = np.exp(-np.exp(-x))
plt.plot(x, F_x)
plt.show()・実行結果
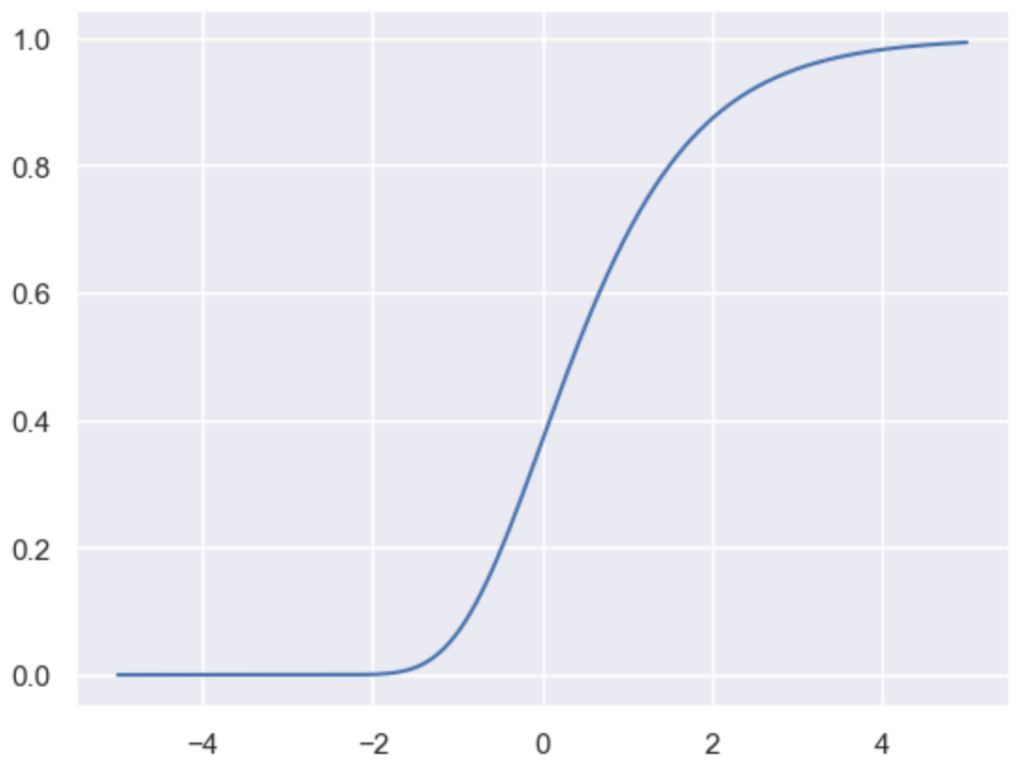
また、下記のように$F(x)$の$x \to -\infty, \, x \to \infty$の極限や、$F(0)$の値を計算することもできる。
$$
\large
\begin{align}
\lim_{x \to -\infty} F(x) &= \lim_{x \to -\infty} \exp{[-\exp{(-x)}]} \\
&= \lim_{s \to \infty} \exp{[-s]} = 0 \\
F(0) &= \exp{[-\exp{(0)}]} \\
&= \exp{(-1)} = \frac{1}{e} = 0.367879 \cdots \\
\lim_{x \to \infty} F(x) &= \lim_{x \to \infty} \exp{[-\exp{(-x)}]} \\
&= \exp{(0)} = 1
\end{align}
$$
ガンベル分布と逆関数法
逆関数法は一様乱数$u \sim \mathrm{Uniform}(0,1)$を累積分布関数$F(x)$の逆関数$F^{-1}(u)$に代入することで$F(x)$に対応する分布に基づく乱数生成を行う手法である。詳しくは下記などで取り扱った。
ここで$u = F(x) = \exp{[-\exp{(-x)}]}$を$x$について解くと下記が得られる。
$$
\large
\begin{align}
u &= \exp{[-\exp{(-x)}]} \\
\log{u} &= -\exp{(-x)} \\
-\log{u} &= \exp{-x} \\
\log{(-\log{u})} &= -x \\
x &= -\log{(-\log{u})}
\end{align}
$$
上記よりガンベル分布の累積分布関数の逆関数$F^{-1}(u)$は$F^{-1}(u)=-\log{(-\log{u})}$である。よって得られた一様乱数に対し、$F^{-1}(u)=-\log{(-\log{u})}$を計算することでガンベル分布に従う乱数を得ることができる。
ガンベル最大トリックのアルゴリズム・プログラム
$$
\large
\begin{align}
p_{k} = \mathrm{softmax}(a_k) = \frac{\exp{(a_{k})}}{\displaystyle \sum_{i=1}^{N} \exp{a_{i}}}
\end{align}
$$
$a_1, \cdots a_N$が与えられた際に上記の確率$p_k$に基づいて無作為サンプリングを行う際に、$a_1, \cdots a_N$の値によっては$\exp$を計算することで値がオーバーフローを起こす場合がある。
ガンベル最大トリックは「位置パラメータ$0$、尺度パラメータ$1$のガンベル分布に基づいて得られた乱数$G_i$を元に$Z_i=a_i+G_i$とおくとき、$Z_k$が最大である確率が$p_k$に一致すること」に基づく手法である。下記のプログラムを用いることでガンベル最大トリックを用いたサンプリングを行える。
import numpy as np
np.random.seed(0)
a = np.array([3., 7., 5.])
z = np.zeros(len(a))
for n in range(10):
for i in range(len(a)):
u_i = np.random.rand()
g_i = -np.log(-np.log(u_i))
z[i] = a[i] + g_i
k = np.argmax(z)+1
print(k)・実行結果
2
2
2
2
2
3
2
2
2
2上記では$i=2$が多く得られる結果が観測された。ここで$i=1$〜$i=3$のそれぞれの確率は下記のように計算できる。
import numpy as np
a = np.array([3., 7., 5.])
p = np.exp(a)/np.sum(np.exp(a))
print(p)[ 0.01587624 0.86681333 0.11731043]上記より$p_1=0.01587624, \, p_2=0.86681333, \, p_3=0.11731043$であるので、サンプリング結果は概ね適切であることが確認できる。
ガンベル最大トリックの導出
$G_k=g_k$のとき$Z_k$が最大である条件付き確率
$G_k$を$G_k=g_k$で固定するとき、$Z_k=a_k+g_k$が$Z_i$より大きい確率$P(Z_i<Z_k)$は下記のように表せる。
$$
\large
\begin{align}
P(Z_i < a_k+g_k) &= P(a_i+G_i < a_k+g_k) \\
&= P(G_i < a_k-a_i+g_k) \quad (1)
\end{align}
$$
このとき$G_i$がガンベル分布に従うので$(1)$式は下記のように表せる。
$$
\large
\begin{align}
P(Z_i < Z_k) &= P(G_i < a_k-a_i+g_k) \quad (1) \\
&= F(a_k – a_i + g_k) \quad (2)
\end{align}
$$
ここで$G_i$は独立同分布($\mathrm{i.i.d.}$)に基づいてサンプリングされるので、$i \neq k$のすべての$i$について$Z_i < Z_k$が成立する確率は下記のように表せる。
$$
\large
\begin{align}
P(\max{(Z_1, \cdots , Z_N)}=Z_k|G_k=g_k) = \prod_{i \neq k} F(a_k – a_i + g_k) \quad (3)
\end{align}
$$
$G_k$に関する周辺化
以下、$(3)$式を$G_k=g_k$について周辺化を行う。
$$
\begin{align}
P(\max{(Z_1, \cdots , Z_N)}=Z_k) &= \int_{-\infty}^{\infty} P(\max{(Z_1, \cdots , Z_N)}=Z_k|G_k=g_k) P(G_k=g_k) d g_k \\
&= \int_{-\infty}^{\infty} f(g_k) \prod_{i \neq k} F(a_k-a_i+g_k) d g_k \\
&= \int_{-\infty}^{\infty} \exp{(-g_k)} F(g_k) \prod_{i \neq k} F(a_k-a_i+g_k) d g_k \\
&= \int_{-\infty}^{\infty} \exp{(-g_k)} F(a_k-a_k+g_k) \prod_{i \neq k} F(a_k-a_i+g_k) d g_k \\
&= \int_{-\infty}^{\infty} \exp{(-g_k)} \prod_{i=1}^{N} F(a_k-a_i+g_k) d g_k \\
&= \int_{-\infty}^{\infty} \exp{(-g_k)} \prod_{i=1}^{N} \exp{(-\exp{[-(a_k-a_i+g_k)]})} d g_k \\
&= \int_{-\infty}^{\infty} \exp{(-g_k)} \exp{ \left( – \sum_{i=1}^{N} \exp{[-(a_k-a_i+g_k)]} \right)} d g_k \\
&= \int_{-\infty}^{\infty} \exp{(-g_k)} \exp{ \left( – \sum_{i=1}^{N} \frac{\exp{a_i}\exp{(-g_k)}}{\exp{a_k}} \right)} d g_k \\
&= \int_{-\infty}^{\infty} \exp{(-g_k)} \exp{ \left( – \exp{(-g_k)} \frac{\sum_{i=1}^{N} \exp{a_i}}{\exp{a_k}} \right)} d g_k \\
&= \int_{-\infty}^{\infty} \exp{(-g_k)} \exp{ \left( – \frac{\exp{-g_k}}{p_k} \right)} d g_k \\
&= \int_{-\infty}^{\infty} \exp{(-x)} \exp{ \left( – \frac{\exp{-x}}{p_k} \right)} dx \\
&= \left[ p_{k} \exp{\left( -\frac{\exp{(-x)}}{p_{k}} \right)} \right]_{-\infty}^{\infty} \\
&= p_{k} \exp{(0)} = p_k
\end{align}
$$
上記より、$Z_k$が最大である確率が$p_k$に一致することが確認できる。また、積分にあたっては下記が成立することを用いた。
$$
\large
\begin{align}
\frac{d}{dx} \left[ p_{k} \exp{\left( -\frac{\exp{(-x)}}{p_{k}} \right)} \right] &= \cancel{p_{k}} \exp{\left( -\frac{\exp{(-x)}}{p_{k}} \right)} \times -\frac{\exp{(-x)}}{\cancel{p_{k}}} \times (-1) \\
&= \exp{(-x)} \exp{ \left( – \frac{\exp{-x}}{p_k} \right)}
\end{align}
$$
