ガンマ乱数の生成とその応用 〜ガンマ分布、$\chi^2$分布に基づく乱数の生成〜

当記事ではガンマ分布に基づくガンマ乱数の生成とその応用にあたって$\chi^2$分布に基づく乱数の生成を行います。ガンマ分布の形状パラメータと尺度パラメータに特定の値を定めることで、指数分布や$\chi^2$分布が導出できるので合わせて抑えておくと良いと思います。

一様乱数の生成などの他の乱数生成の手法に関しては下記で取りまとめを行いましたので、こちらも合わせてご確認ください。
https://www.hello-statisticians.com/explain-terms-cat/random_sampling1.html

「自然科学の統計学」の$11.4.3$節を参考に作成を行いました。

自然科学の統計学 (基礎統計学)

3,190円(04/23 14:26時点)

Amazon

また、ガンマ分布と標本分布に関しては「現代数理統計学」の$4$章の「統計量と標本分布」なども合わせて参照すると良いと思います。

新装改訂版 現代数理統計学

竹村 彰通

2,970円(04/23 19:42時点)

Amazon

ガンマ分布

ガンマ分布の確率密度関数

ガンマ分布$\mathrm{Ga}(\alpha,\beta)$の確率密度関数$f(x)$を下記のように定められる。
$$
\large
\begin{align}
f(x) = \frac{1}{\beta^{\alpha} \Gamma(\alpha)} x^{\alpha-1} e^{-\frac{x}{\beta}} \quad (1)
\end{align}
$$

上記の$\alpha$と$\beta$はガンマ分布のパラメータであり、それぞれ形状パラメータ、尺度パラメータという。ここで尺度パラメータ$\beta$を元に$\mathrm{Ga}(\alpha,\beta)$と表すか、$\lambda=1/\beta$のように逆数を考え、$\mathrm{Ga}(\alpha,\lambda)$のように表すかは書籍によって異なるので注意が必要である。以下では$\mathrm{Ga}(\alpha,\beta)$、$\mathrm{Ga}(\alpha,\lambda)$の文字に着目して下記のように使い分けを行う。
$$
\large
\begin{align}
f(x) &= \frac{1}{\beta^{\alpha} \Gamma(\alpha)} x^{\alpha-1} e^{-\frac{x}{\beta}} \quad (1) \\
f(x) &= \frac{\lambda^{\alpha}}{\Gamma(\alpha)} x^{\alpha-1} e^{-\lambda x} \quad (1)’
\end{align}
$$

また、$\Gamma(\alpha)$はガンマ関数であり、ガンマ分布の正規化にあたって用いられる。ガンマ関数は下記のように定義される。
$$
\large
\begin{align}
\Gamma(\alpha) = \int_{0}^{\infty} t^{\alpha-1} e^{-t} dt \quad (2)
\end{align}
$$

ここで上記に対し、$t = \lambda x$で変数変換を行うことを考える。$\displaystyle \frac{dt}{dx}=\lambda$より、$(2)$式は下記のように変形できる。
$$
\large
\begin{align}
\Gamma(\alpha) &= \int_{0}^{\infty} t^{\alpha-1} e^{-t} dt \quad (2) \\
\Gamma(\alpha) &= \int_{0}^{\infty} (\beta x)^{\alpha-1} e^{-\lambda x} \frac{dt}{dx} dx \\
\Gamma(\alpha) &= \beta^{\alpha-1} \int_{0}^{\infty} x^{\alpha-1} e^{-\lambda x} \times \lambda dx \\
\Gamma(\alpha) &= \lambda^{\alpha} \int_{0}^{\infty} x^{\alpha-1} e^{-\lambda x} dx \\
\frac{\Gamma(\alpha)}{\lambda^{\alpha}} &= \int_{0}^{\infty} x^{\alpha-1} e^{-\lambda x} dx \quad (3)
\end{align}
$$

$(3)$式は積分に関する導出にあたってよく出てくるので抑えておくと良い。また、$(3)$式より、$(1)’$式が正規化されていることも確認できる。

形状パラメータ・尺度パラメータと分布の形状

ガンマ分布$\mathrm{Ga}(\alpha,\beta)$の確率密度関数の形状が、形状パラメータ$\alpha$と尺度パラメータ$\beta$の値の変化によってどのように変化するかに関して以下では確認を行う。

ガンマ分布の確率密度関数の計算を行うにあたってはガンマ関数$\Gamma(\alpha)$の値を計算する必要がある。ガンマ関数に関しては$\alpha$が$1$以上の整数であるときに$\Gamma(\alpha)=(\alpha-1)!$が成立するので、以下では$\alpha=2,3,5$のそれぞれに関して$\beta=0.5,1$の確認を行う。

import math
import numpy as np
import matplotlib.pyplot as plt

alpha = np.array([2., 3., 5.])
beta = np.array([0.5, 1.])

x = np.arange(0., 8.1, 0.1)

for i in range(alpha.shape[0]):
    for j in range(beta.shape[0]):
        f_x = x**(alpha[i]-1) * np.e**(-x/beta[j]) /(beta[j]**alpha[i] * math.factorial(alpha[i]-1))
        plt.plot(x,f_x,label="alpha: {}, beta: {}".format(alpha[i],beta[j]))

plt.legend()
plt.show()

・実行結果

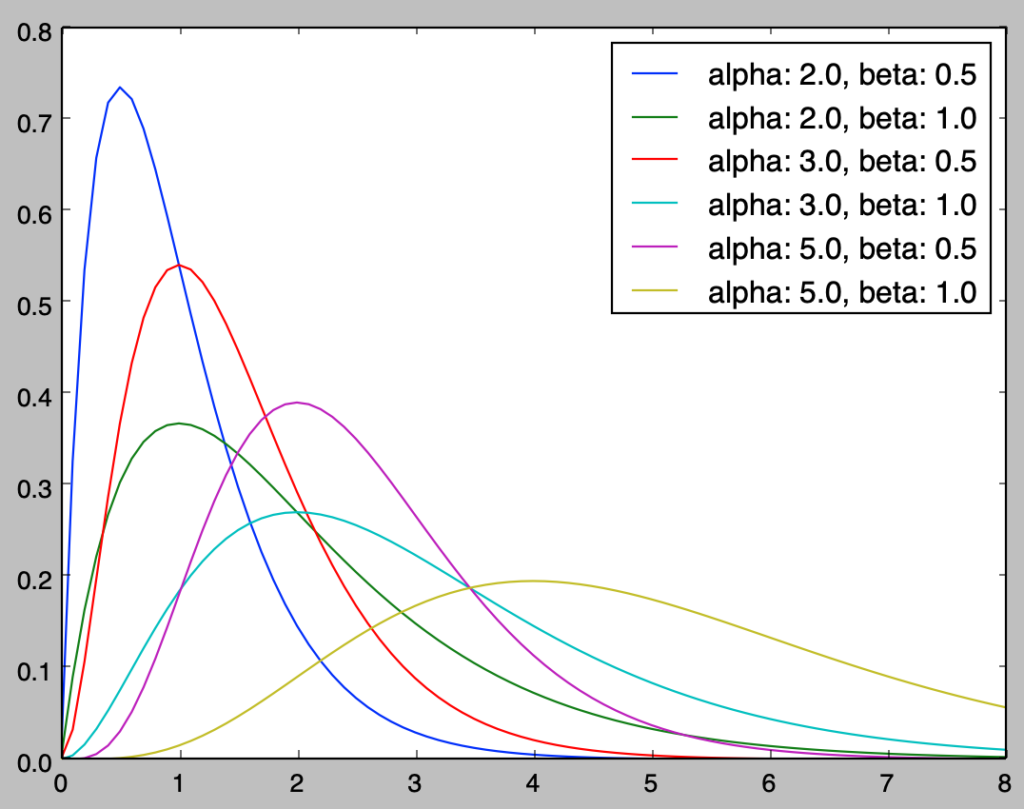
上記の「青、赤、紫」や「緑、水色、黄色」を確認すると、$\alpha$が大きくなるにつれて分布の中心が右にシフトしていることが確認できる。同様に「青と緑」、「赤と水色」、「紫と黄色」を確認することで$\beta$が大きくなるにつれて分布の中心が右にシフトしていることが確認できる。

この解釈にあたっては$\alpha$は多項式の次数であり、指数関数の減少分に対しどこまで対応できるかの指標であると考えると良い。また、$\beta$は指数関数の減少の速さを制御するパラメータだと考えると良い。

ここまでの内容により、多項式の次数に対応する形状パラメータ$\alpha$が大きいと分布は右にシフトし、指数関数の減少の速さに対応する尺度パラメータ$\beta$が大きいと分布が右にシフトすることについて把握することができる。

ガンマ分布と指数分布

ガンマ分布$\mathrm{Ga}(\alpha,\beta)$の形状パラメータと尺度パラメータが$\alpha=1,\beta=1/\lambda$のように与えられる場合、$(1)$式で表される確率密度関数$f(x)$は下記のように考えられる。
$$
\large
\begin{align}
f(x) &= \frac{1}{\beta^{\alpha} \Gamma(\alpha)} x^{\alpha-1} e^{-\frac{x}{\beta}} \quad (1) \\
&= \frac{\lambda^{1}}{\Gamma(1)} x^{1-1} e^{-\lambda x} \\
&= \frac{\lambda}{0!} x^{0} e^{-\lambda x} \\
&= \frac{\lambda}{1} \times 1 \times e^{-\lambda x} \\
&= \lambda e^{-\lambda x}
\end{align}
$$

上記は指数分布$\mathrm{Ex}(\lambda)$に一致する。よって指数分布はガンマ分布の特殊な場合と考えることができる。前項のガンマ分布のプログラムを元に、指数分布のグラフは下記のように作成できる。

import math
import numpy as np
import matplotlib.pyplot as plt

alpha = np.array([1.])
lamb = np.array([1., 2., 3.])

x = np.arange(0., 3.1, 0.1)

for i in range(alpha.shape[0]):
    for j in range(lamb.shape[0]):
        f_x = lamb[j]**alpha[i] * x**(alpha[i]-1) * np.e**(-lamb[j]*x) / math.factorial(alpha[i]-1)
        plt.plot(x,f_x,label="alpha: {}, lambda: {}".format(alpha[i],lamb[j]))

plt.legend()
plt.show()

・実行結果

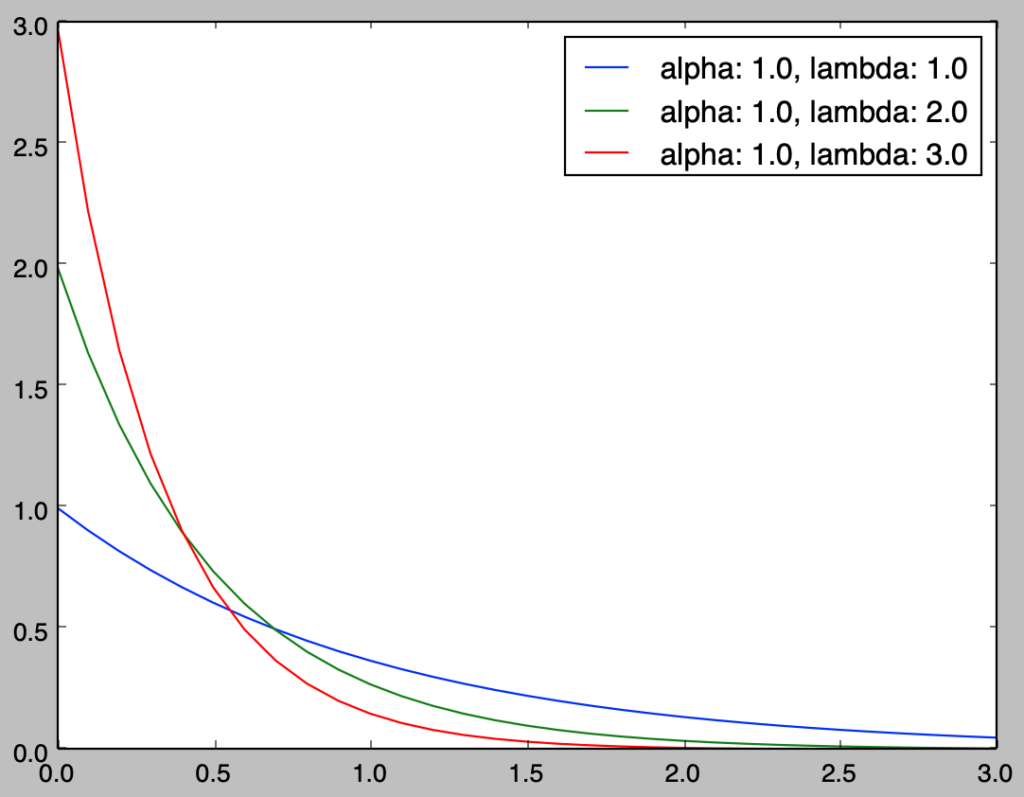
前項で取り扱ったガンマ分布をさらに左にシフトさせたグラフが得られたことが確認できる。また、前項と当項では$x=0$を考慮したが、$0<\alpha<1$では$x=0$の値が計算できないので$x>0$でグラフ描画の計算を行う必要がある。

ガンマ分布と$\chi^2$分布

自由度$1$の$\chi^2$分布がガンマ分布$\displaystyle \mathrm{Ga}(\alpha,\beta) = \mathrm{Ga} \left(\frac{1}{2},2\right)$で表せることを以下に示す。

まずは標準正規分布の確率密度関数の$f(x)$を考える。$f(x)$は下記のように表せる。
$$
\large
\begin{align}
f(x) = \mathcal{N}(x|0,1) = \frac{1}{\sqrt{2 \pi}} \exp \left( -\frac{x^2}{2} \right)
\end{align}
$$

上記に対し、$x \geq 0$で$y=x^2$のように変数変換を行うことを考える。このとき$x \geq 0$であるので、$x = \sqrt{y} \geq 0$が成立する。ここで$\displaystyle \frac{dx}{dy}$は下記のように計算できる。
$$
\large
\begin{align}
\frac{dx}{dy} &= \frac{d}{dy} (y)^{\frac{1}{2}} \\
&= \frac{1}{2 \sqrt{y}}
\end{align}
$$

よって$y$に対応する確率密度関数を$g(y)$とおくと、$g(y)$は下記のように表せる。
$$
\large
\begin{align}
g(y) &= f(x)\frac{dx}{dy} \\
&= \frac{1}{\sqrt{2 \pi}} \exp \left( -\frac{y}{2} \right) \times \frac{1}{2 \sqrt{y}} \\
&= \frac{1}{2} \times \frac{1}{\sqrt{2 \pi}} y^{\frac{1}{2}-1} \exp \left( -\frac{y}{2} \right)
\end{align}
$$

上記は$x \geq 0$のみを考えたので、$\chi^2$分布の確率密度関数$f_2(y)$は$f_2(y)=2g(y)$で得られる。ここで$f_2(y)=2g(y)$は下記のように変形できる。
$$
\large
\begin{align}
f_2(y) &= 2g(y) = \frac{2}{2} \times \frac{1}{\sqrt{2 \pi}} y^{\frac{1}{2}-1} \exp \left( -\frac{y}{2} \right) \\
&= \frac{1}{\sqrt{2 \pi}} y^{\frac{1}{2}-1} \exp \left( -\frac{y}{2} \right) \\
&= \frac{1}{\displaystyle 2^{\frac{1}{2}} \Gamma \left( \frac{1}{2} \right)} y^{\frac{1}{2}-1} \exp \left( -\frac{y}{2} \right)
\end{align}
$$

上記はガンマ分布$\displaystyle \mathrm{Ga} \left(\frac{1}{2},2\right)$の確率密度関数に一致する。また、次項で取り扱う「ガンマ分布の再生性」を用いることで、自由度$\nu$のガンマ分布が$\displaystyle \mathrm{Ga} \left(\frac{\nu}{2},2\right)$であることも示せる。

ガンマ分布の再生性

$X_1 \sim \mathrm{Ga}(\alpha_1,\beta), X_2 \sim \mathrm{Ga}(\alpha_2,\beta)$のとき、$X_1+X_2 \sim \mathrm{Ga}(\alpha_1+\alpha_2,\beta)$が成立する。詳細は「現代数理統計学」の演習$3.8$の解答で取り扱った。

ガンマ分布の再生性より、$\displaystyle X_i \sim \mathrm{Ga} \left( \frac{1}{2}, 2 \right)$のとき、下記が成立する。
$$
\large
\begin{align}
\sum_{i=1}^{\nu} X_i \sim \mathrm{Ga} \left( \frac{\nu}{2}, 2 \right)
\end{align}
$$

上記より、自由度$\nu$の$\chi^2$分布はガンマ分布$\displaystyle \mathrm{Ga} \left( \frac{\nu}{2}, 2 \right)$であることが示せる。

Pythonを用いたガンマ乱数の生成

仕組みの確認

「指数分布と逆関数法」の対応では一様乱数の$U \sim \mathrm{Uniform}(0,1)$を元に$\displaystyle X = -\frac{1}{\lambda}\log{U}$を計算することで指数分布$\mathrm{Ex}(\lambda)$を元にサンプリングできることの確認を行なった。

ここで当記事では$\displaystyle \beta = \frac{1}{\lambda}$のように定義したので、$\displaystyle X = -\beta\log{U} \sim \mathrm{Ga}(1,\beta)$であると考えられる。

以下、形状パラメータ$\alpha$の値に関して場合分けを行い、それぞれのサンプリング法について確認を行う。

ガンマ分布の形状パラメータ$\alpha$が整数の場合のサンプリング

「ガンマ分布の再生性」より、$\displaystyle X_i \sim \mathrm{Ga}(1,\beta)$であることに基づいて下記が成立する。
$$
\large
\begin{align}
\sum_{i=1}^{n} X_i \sim \mathrm{Ga}(n, \beta)
\end{align}
$$

したがって、下記を計算することでガンマ分布$\mathrm{Ga}(n, \beta)$を元にサンプリングを行える。
$$
\large
\begin{align}
\sum_{i=1}^{n} X_i &= -\sum_{i=1}^{n} \beta\log{U_i} \\
&= -\beta \log{ \left[ \prod_{i=1}^{n} U_i \right] }
\end{align}
$$

ガンマ分布の形状パラメータ$\alpha$が$($整数$+1/2)$の場合のサンプリング

前節の「ガンマ分布と$\chi^2$分布」より、$Z \sim \mathcal{N}(0,1)$のとき、$\displaystyle Z^2 \sim \mathrm{Ga} \left(\frac{1}{2},2\right)$が成立する。また、下記も同時に成り立つ。
$$
\large
\begin{align}
\frac{\beta}{2}Z^2 \sim \mathrm{Ga} \left(\frac{1}{2},\beta\right)
\end{align}
$$

よって、下記を計算することでガンマ分布$\displaystyle \mathrm{Ga} \left(n+\frac{1}{2},\beta\right)$を元にサンプリングを行える。
$$
\large
\begin{align}
\sum_{i=1}^{n} X_i + \frac{\beta}{2}Z^2 = -\beta \log{ \left[ \prod_{i=1}^{n} U_i \right] } + \frac{\beta}{2}Z^2
\end{align}
$$

詳しい導出は下記の演習で取り扱った。

Pythonを用いたサンプリング

$\alpha=5,\beta=1$のサンプリングのプログラム

以下、ガンマ分布$\mathrm{Ga}(\alpha,\beta) = \mathrm{Ga}(5,1)$に基づくサンプリングを行う。

import numpy as np
import matplotlib.pyplot as plt
import math

np.random.seed(0)

alpha = 5
num_samples = 1000
beta = 1.

x = np.arange(0.,15.1,0.1)
y = x**(alpha-1) * np.e**(-x/beta) / (beta**(alpha) * math.factorial(alpha-1))

U = np.random.rand(num_samples, alpha)
X = np.zeros(num_samples)

for i in range(U.shape[0]):
    U_ = 1.
    for j in range(U.shape[1]):
        U_ *= U[i,j]
    X[i] = -beta*np.log(U_)

plt.subplot(211)
plt.plot(x,y,color="green")
plt.subplot(212)
plt.hist(X,bins=50,color="limegreen")
plt.xlim([0.,15.])
plt.show()

・実行結果

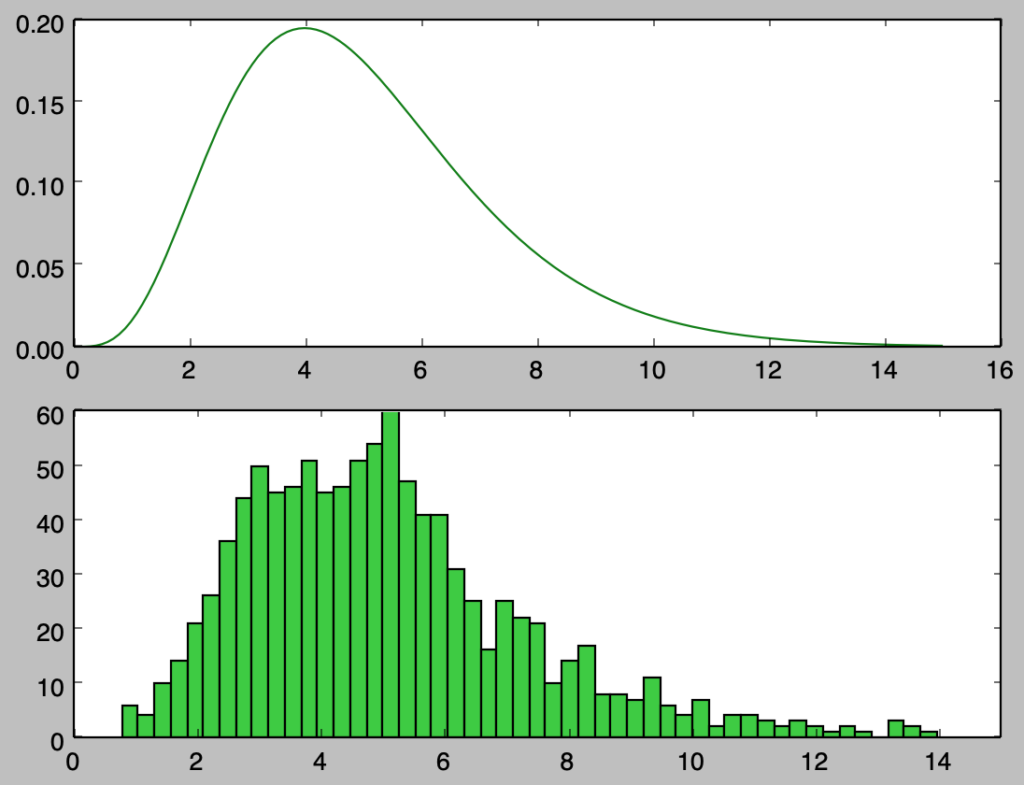
上記を確認すると、概ね確率密度関数と同様のサンプリングを行えたことが確認できる。上記は$1,000$個のサンプルに対応するので、以下ではさらに確認するにあたって$100,000$個のサンプルの生成を行う。

np.random.seed(0)

alpha = 5
num_samples = 100000
beta = 1.

x = np.arange(0.,15.1,0.1)
y = x**(alpha-1) * np.e**(-x/beta) / (beta**(alpha) * math.factorial(alpha-1))

U = np.random.rand(num_samples, alpha)
X = np.zeros(num_samples)

for i in range(U.shape[0]):
    U_ = 1.
    for j in range(U.shape[1]):
        U_ *= U[i,j]
    X[i] = -beta*np.log(U_)

plt.subplot(211)
plt.plot(x,y,color="green")
plt.subplot(212)
plt.hist(X,bins=50,color="limegreen")
plt.xlim([0.,15.])
plt.show()

・実行結果

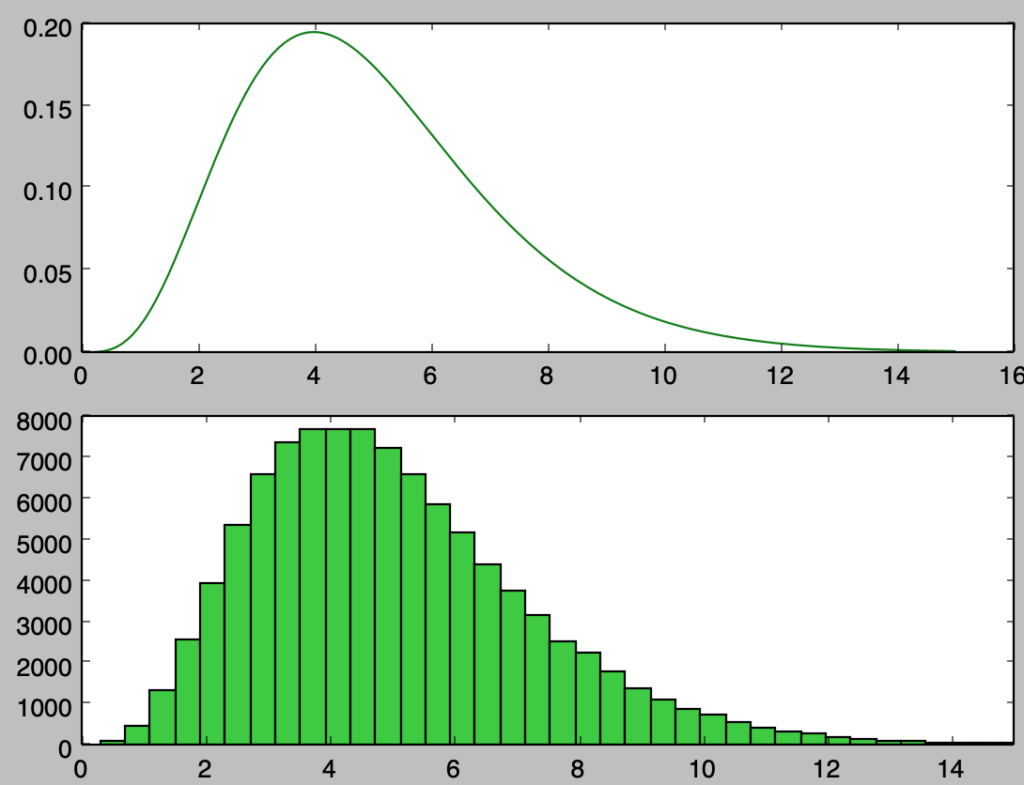
$\displaystyle \alpha=5+\frac{1}{2},\beta=1$のサンプリングのプログラム

以下、ガンマ分布$\displaystyle \mathrm{Ga}(\alpha,\beta) = \mathrm{Ga}\left(5+\frac{1}{2},1\right)$に基づくサンプリングを行う。

import numpy as np
import matplotlib.pyplot as plt
import math
from scipy import stats

np.random.seed(0)

alpha = 5.5
num_samples = 1000
beta = 1.

x = np.arange(0.,15.1,0.1)
y = x**(alpha-1) * np.e**(-x/beta) / (beta**(alpha) * math.factorial(int(alpha)-1) * np.sqrt(np.pi))

U = np.random.rand(num_samples, alpha)
X = np.zeros(num_samples)

for i in range(U.shape[0]):
    U_ = 1.
    for j in range(U.shape[1]):
        U_ *= U[i,j]
    X[i] = -beta*np.log(U_)

X += stats.norm.rvs(size=num_samples)**2

plt.subplot(211)
plt.plot(x,y,color="green")
plt.subplot(212)
plt.hist(X,bins=50,color="limegreen")
plt.xlim([0.,15.])
plt.show()

・実行結果

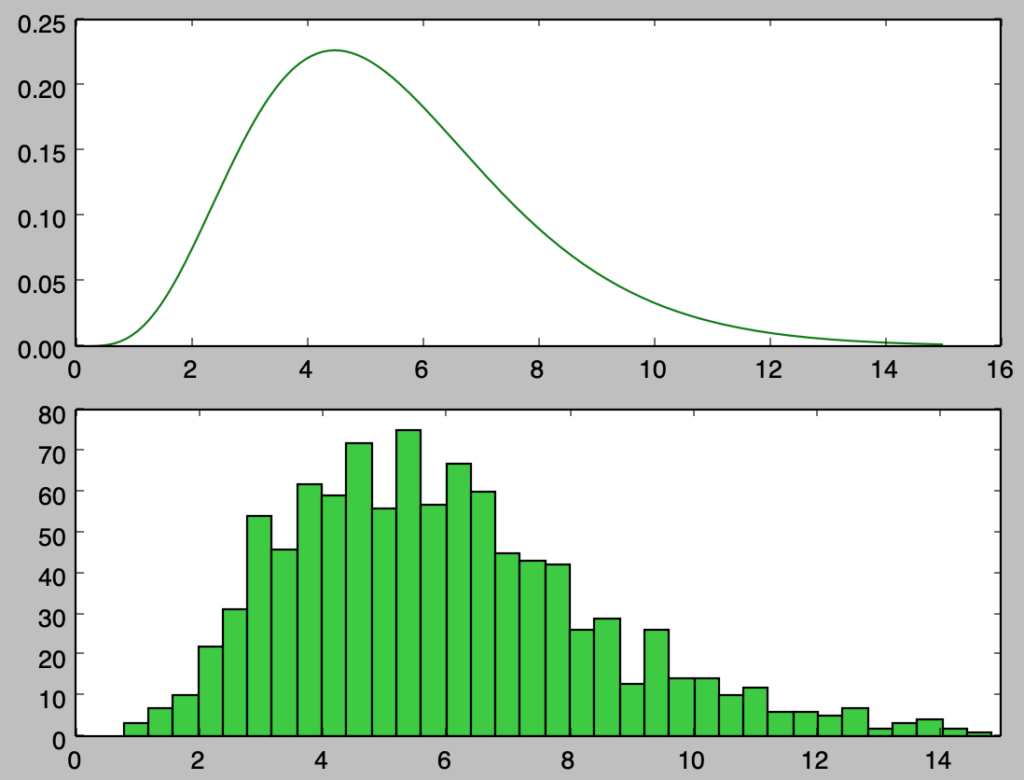
上記を確認すると、概ね確率密度関数と同様のサンプリングを行えたことが確認できる。以下ではさらに確認するにあたって$100,000$個のサンプルの生成を行う。

np.random.seed(0)

alpha = 5.5
num_samples = 100000
beta = 1.

x = np.arange(0.,15.1,0.1)
y = x**(alpha-1) * np.e**(-x/beta) / (beta**(alpha) * math.factorial(int(alpha)-1) * np.sqrt(np.pi))

U = np.random.rand(num_samples, alpha)
X = np.zeros(num_samples)

for i in range(U.shape[0]):
    U_ = 1.
    for j in range(U.shape[1]):
        U_ *= U[i,j]
    X[i] = -beta*np.log(U_)

X += stats.norm.rvs(size=num_samples)**2

plt.subplot(211)
plt.plot(x,y,color="green")
plt.subplot(212)
plt.hist(X,bins=50,color="limegreen")
plt.xlim([0.,15.])
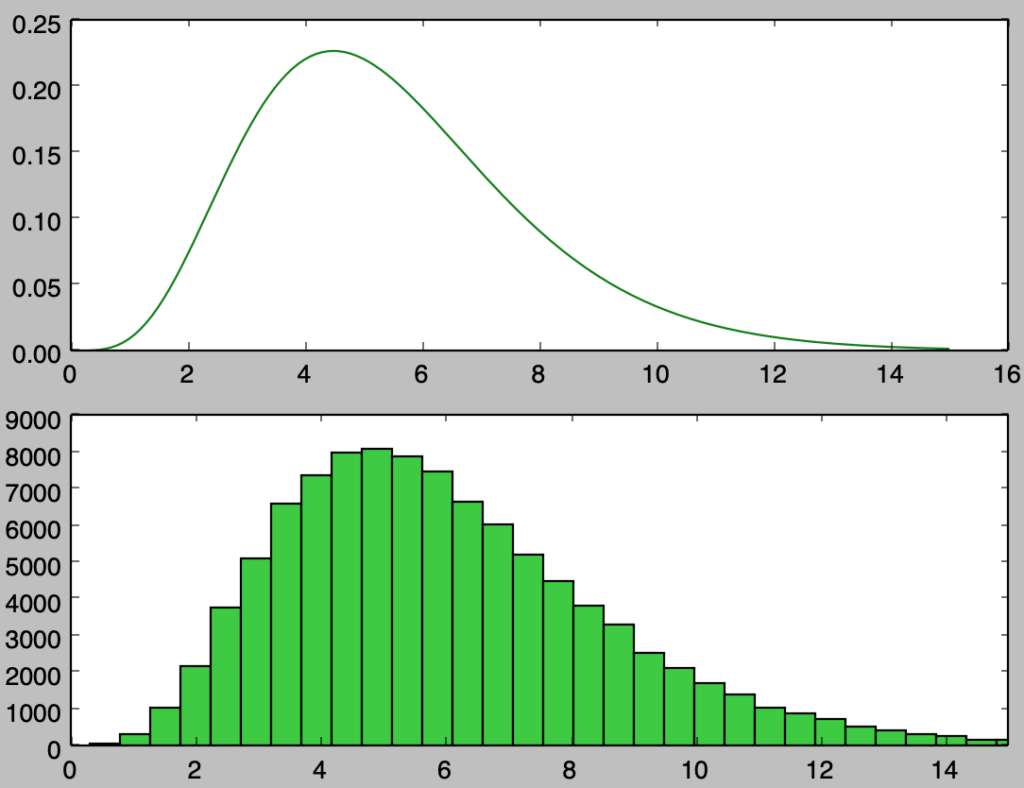
plt.show()

・実行結果