Ch.3 「多次元の確率変数」の章末問題の解答例　〜現代数理統計学(学術図書出版社)〜

当記事は「現代数理統計学(学術図書出版社)」の読解サポートにあたってChapter.3の「多次元の確率変数」の章末問題の解説について行います。

基本的には書籍の購入者向けの解説なので、まだ入手されていない方は購入の上ご確認ください。また、解説はあくまでサイト運営者が独自に作成したものであり、書籍の公式ページではないことにご注意ください。（そのため著者の意図とは異なる解説となる可能性はあります）

↓下記が公式の解答なので、正確にはこちらを参照ください。
https://www.gakujutsu.co.jp/text/isbn978-4-7806-0860-1/

章末の演習問題について

問題3.1の解答例

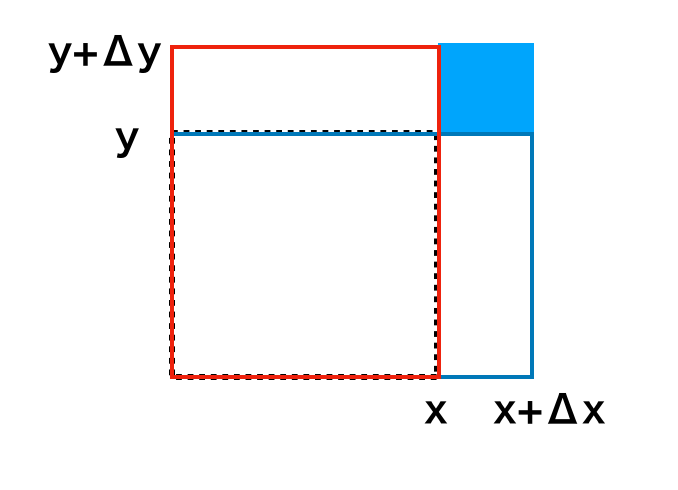
上図のように考えることで示すことができる。

問題3.2の解答例

$$
\large
\begin{align}
F(x_1, x_2, …, x_n) = F(x_1)F(x_2)…F(x_n) \quad (1)
\end{align}
$$
$(1)$式から離散分布の場合$(3.6)$式、連続分布の場合$(3.14)$式を示せばよい。

・連続分布の場合
$(1)$の両辺を$x_1, x_2, …, x_n$で微分することを考える。
$$
\large
\begin{align}
\frac{\partial}{\partial x_1}…\frac{\partial}{\partial x_n} F(x_1, x_2, …, x_n) &= \frac{\partial}{\partial x_1}…\frac{\partial}{\partial x_n}F(x_1)F(x_2)…F(x_n) \\
f(x_1, x_2, …, x_n) &= \prod_{i=1}^{n} \frac{\partial}{\partial x_i} F(x_i) \\
&= \prod_{i=1}^{n} f(x_i)
\end{align}
$$
上記は$(3.14)$式と同義である。

・離散分布の場合
$(3.9)$式、$(3.10)$式を考えることで連続分布の場合と同様に(3.6)式を導出できる。

問題3.3の解答例

$(3.29)$式より、$r$と$\theta$が独立かつ、$\theta$は$0 \leq \theta \leq 2\pi$の一様分布に従うことがわかる。

また、$v=r^2$を用いて変数変換を行うことを考える。変換後を$g(v,\theta)$のようにおくと、下記のように計算を行うことができる。
$$
\large
\begin{align}
g(v,\theta) &= f(r,\theta) \frac{dr}{dv} \\
&= f(\sqrt{v},\theta) \times \frac{1}{2 \sqrt{v}} \\
&= c^2 \sqrt{v} \exp \left( -\frac{v}{2} \right) \times \frac{1}{2 \sqrt{v}} \\
&= \frac{c^2}{2} \exp \left( -\frac{v}{2} \right) \\
& \propto \exp \left( -\frac{v}{2} \right)
\end{align}
$$
上記より、$r^2$は指数分布$Ex(2)$に従うことがわかる。

問題3.4の解答例

問題3.5の解答例

$Z = a_1X_1 + a_2X_2 + … + a_nX_n$を考えた際、$Z$の分散$V[Z]$は分散の定義より下記のように表すことができる。
$$
\large
\begin{align}
V[Z] &= E[(Z-E[Z])^2] \\
&= E[(a_1X_1 + a_2X_2 + … + a_nX_n-E[a_1X_1 + a_2X_2 + … + a_nX_n])^2] \\
&= E[((a_1X_1-E[a_1X_1])+…+(a_nX_n-E[a_nX_n]))^2] \\
&= E[(a_1(X_1-E[X_1])+…+a_n(X_n-E[X_n]))^2] \\
&= E \left[ \sum_{i=1}^{n} a_i^2(X_i-E[X_i])^2 + 2\sum_{i<j} a_ia_j(X_i-E[X_i])(X_j-E[X_j]) \right] \\
&= E \left[ \sum_{i=1}^{n} a_i^2(X_i-E[X_i])^2 \right] + 2 E \left[ \sum_{i<j} a_ia_j(X_i-E[X_i])(X_j-E[X_j]) \right] \\
&= \sum_{i=1}^{n} a_i^2 E[(X_i-E[X_i])^2] + 2 \sum_{i<j} a_ia_j E[(X_i-E[X_i])(X_j-E[X_j])] \\
&= \sum_{i=1}^{n} a_i^2 V[X_i] + 2 \sum_{i<j} a_ia_j Cov(X_i,X_j)
\end{align}
$$

上記より、式$(3.37)$が成立することを示すことができる。

問題3.6の解答例

$$
\large
\begin{align}
\mathbf{X} = \left(\begin{array}{c} X_1 \\ … \\ X_n \end{array} \right)
\end{align}
$$

上記のように$n$次元確率ベクトルの$\mathbf{X}$を定義する。$(3.40)$式は$n$次元の定数ベクトル$\mathbf{a}$と$n$次の定数行列$\mathbf{B}$に関して下記のように表される。
$$
\large
\begin{align}
E[\mathbf{a} + \mathbf{B}\mathbf{X}] = \mathbf{a} + \mathbf{B}E[\mathbf{X}] \quad (1)
\end{align}
$$

以下、上記の$(1)$式を示す。
$\mathbf{a} + \mathbf{B}\mathbf{X}$は下記のように計算できる。
$$
\large
\begin{align}
\mathbf{a} + \mathbf{B}\mathbf{X} &= \left(\begin{array}{c} a_1 \\ … \\ a_n \end{array} \right) + \left(\begin{array}{ccc} B_{11} & … & B_{1n} \\ … & … & … \\ B_{n1} & … & B_{nn} \end{array} \right) \left(\begin{array}{c} X_1 \\ … \\ X_n \end{array} \right) \\
&= \left(\begin{array}{c} a_1 + B_{11}X_1+B_{12}X_2+…+B_{1n}X_n \\ … \\ a_n + B_{n1}X_1+B_{n2}X_2+…+B_{nn}X_n \end{array} \right)
\end{align}
$$

上記の期待値を取ることで、$E[\mathbf{a} + \mathbf{B}\mathbf{X}]$は下記のように表せる。
$$
\large
\begin{align}
E[ \mathbf{a} + \mathbf{B}\mathbf{X} ] &= E \left[ \left(\begin{array}{c} a_1 + B_{11}X_1+B_{12}X_2+…+B_{1n}X_n \\ … \\ a_n + B_{n1}X_1+B_{n2}X_2+…+B_{nn}X_n \end{array} \right) \right] \\
&= \left(\begin{array}{c} a_1 + E[ B_{11}X_1+B_{12}X_2+…+B_{1n}X_n ] \\ … \\ a_n + E[ B_{n1}X_1+B_{n2}X_2+…+B_{nn}X_n ] \end{array} \right) \\
&= \left(\begin{array}{c} a_1 + B_{11}E[X_1]+B_{12}E[X_2]+…+B_{1n}E[X_n] \\ … \\ a_n + B_{n1}E[X_1]+B_{n2}E[X_2]+…+B_{nn}E[X_n] \end{array} \right) \\
&= \mathbf{a} + \left( \begin{array}{c} B_{11}E[X_1]+B_{12}E[X_2]+…+B_{1n}E[X_n] \\ … \\ B_{n1}E[X_1]+B_{n2}E[X_2]+…+B_{nn}E[X_n] \end{array} \right) \\
&= \mathbf{a} + \mathbf{B} E[\mathbf{X}]
\end{align}
$$

上記より$(1)$式は示すことができる。

問題3.7の解答例

・$(3.42)$式の導出
$$
\large
\begin{align}
\mathbf{X} = \left(\begin{array}{c} X_1 \\ … \\ X_n \end{array} \right), \quad \mathbf{\mu} = \left(\begin{array}{c} \mu_1 \\ … \\ \mu_n \end{array} \right)
\end{align}
$$
上記のように$\mathbf{X}, \mathbf{\mu}$を定義する。このとき、$(\mathbf{X}-\mathbf{\mu})(\mathbf{X}-\mathbf{\mu})^{T}$は下記のように表すことができる。
$$
\large
\begin{align}
(\mathbf{X}-\mathbf{\mu})(\mathbf{X}-\mathbf{\mu})^{T} &= \left(\begin{array}{c} X_1-\mu_1 \\ … \\ X_n-\mu_n \end{array} \right) \left(\begin{array}{ccc} X_1-\mu_1 & … & X_n-\mu_n \end{array} \right) \\
&= \left(\begin{array}{ccc} (X_1-\mu_1)^2 & … & (X_1-\mu_1)(X_n-\mu_n) \\ … & … & … \\ (X_n-\mu_n)(X_1-\mu_1) & … & (X_n-\mu_n)^2 \end{array} \right)
\end{align}
$$

上記の両辺の期待値を取り、$E[(\mathbf{X}-\mathbf{\mu})(\mathbf{X}-\mathbf{\mu})^{T}]$を考えると下記のように変形できる。
$$
\large
\begin{align}
E[(\mathbf{X}-\mathbf{\mu})(\mathbf{X}-\mathbf{\mu})^{T}] &= E \left[ \left(\begin{array}{ccc} (X_1-\mu_1)^2 & … & (X_1-\mu_1)(X_n-\mu_n) \\ … & … & … \\ (X_n-\mu_n)(X_1-\mu_1) & … & (X_n-\mu_n)^2 \end{array} \right) \right] \\
&= \left(\begin{array}{ccc} E[(X_1-\mu_1)^2] & … & E[(X_1-\mu_1)(X_n-\mu_n)] \\ … & … & … \\ E[(X_n-\mu_n)(X_1-\mu_1)] & … & E[(X_n-\mu_n)^2] \end{array} \right) \\
&= \left(\begin{array}{ccc} V[X_1] & … & Cov(X_1,X_n) \\ … & … & … \\ Cov(X_n,X_1) & … & V[X_n] \end{array} \right) \\
&= \left(\begin{array}{ccc} \sigma_{11} & … & \sigma_{1n} \\ … & … & … \\ \sigma_{n1} & … & \sigma_{nn} \end{array} \right) \\
&= \Sigma
\end{align}
$$

・$(3.43)$式の導出

問題3.8の解答例

ポアソン分布、正規分布に関する再生性は下記で導出を行なったため省略する。

・ポアソン分布
https://www.hello-statisticians.com/explain-terms-cat/probdist3.html#i-5

・正規分布
https://www.hello-statisticians.com/explain-terms-cat/probdist3.html#i-8

以下、負の二項分布とガンマ分布に関して確認する。

・負の二項分布
https://www.hello-statisticians.com/explain-books-cat/math_stat_practice_ch2.html#28
上記の導出により、負の二項分布の確率母関数は下記のように表せる。
$$
\large
\begin{align}
G(s) = \frac{p^{r}}{(1-sq)^{r}}
\end{align}
$$

ここ負の二項分布のモーメント母関数を$m(t)$とおくと、$m(t)=G(e^t)$より、$m(t)$は下記のように表せる。
$$
\large
\begin{align}
m(t) &= G(s) \\
&= G(e^t) \\
&= \frac{p^{r}}{(1 – q e^t)^{r}}
\end{align}
$$

ここで確率変数$X_1$はパラメータ$p, q=1-p, r_1$の負の二項分布$NB(r_1,p)$に従い、確率変数$X_2$はパラメータ$p, q=1-p, r_2$の負の二項分布$NB(r_2,p)$に従うとする。また、このときのモーメント母関数を$m_{X_1}(t), m_{X_2}(t)$でおくことを考える。これに対して確率変数$X=X_1+X_2$に関するモーメント母関数を$m_{X}(t)$とすると、$m_{X}(t)$は下記のように表すことができる。
$$
\large
\begin{align}
m_{X}(t) &= E[e^{tX}] \\
&= E[e^{t(X_1+X_2)}] \\
&= E[e^{tX_1}]E[e^{tX_2}] \\
&= \frac{p^{r_1}}{(1 – q e^t)^{r_1}} \times \frac{p^{r_2}}{(1 – q e^t)^{r_2}} \\
&= \frac{p^{r_1+r_2}}{(1 – q e^t)^{r_1+r_2}}
\end{align}
$$
上記より、$(3.51)$式の$NB(r_1,p)*NB(r_2,p) = NB(r_1+r_2,p)$が導出できる。

・ガンマ分布
$(2.76)$式より、ガンマ分布$Ga(\nu,\alpha)$のモーメント母関数は下記のように表すことができる。
$$
\large
\begin{align}
m(t) = (1 – \theta \alpha)^{\nu}
\end{align}
$$

ここで確率変数$X_1$はパラメータ$\nu_1, \alpha$のガンマ分布$Ga(\nu_1, \alpha)$に従い、確率変数$X_2$はパラメータ$\nu_2, \alpha$のガンマ分布$Ga(\nu_2, \alpha)$に従うとする。また、このときのモーメント母関数を$m_{X_1}(t), m_{X_2}(t)$でおくことを考える。これに対して確率変数$X=X_1+X_2$に関するモーメント母関数を$m_{X}(t)$とすると、$m_{X}(t)$は下記のように表すことができる。
$$
\large
\begin{align}
m_{X}(t) &= E[e^{tX}] \\
&= E[e^{t(X_1+X_2)}] \\
&= E[e^{tX_1}]E[e^{tX_2}] \\
&= (1 – \theta \alpha)^{\nu_1} (1 – \theta \alpha)^{\nu_2} \\
&= (1 – \theta \alpha)^{\nu_1+\nu_2}
\end{align}
$$

上記より、$(3.51)$式の$Ga(\nu_1, \alpha)*Ga(\nu_2, \alpha) = Ga(\nu_1+\nu_2, \alpha)$が導出できる。

問題3.9の解答例

連続分布の場合に関して以下示す。$x, y$の同時確率密度関数を$f(x,y)$、確率変数$X$に関する周辺密度関数を$f_{X}(x)$と定義する。このとき、$E[g(X,Y)]$は下記のように変形できる。
$$
\large
\begin{align}
E[g(X,Y)] &= \int \int g(x,y) f(x,y) dx dy \\
&= \int \int g(x,y) f(x,y) dy dx \\
&= \int \left( \int g(x,y) \frac{f(x,y)}{f_{X}(x)} dy \right) f_{X}(x) dx \\
&= \int E[g(x,y)|X=x] f_{X}(x) dx \\
&= E[E[g(x,y)|X=x]]
\end{align}
$$

上記より$(3.55)$式を示すことができる。

問題3.10の解答例

$E[(Z-c)^2]$は下記のように変形できる。
$$
\large
\begin{align}
E[(Z-c)^2] &= E[Z^2 – 2Zc + c^2] \\
&= E[Z^2] -2cE[Z] + c^2 \\
&= (c-E[Z])^2 + E[Z^2] – (E[Z])^2
\end{align}
$$

$(c-E[Z])^2$は$c$に関して下に凸の二次関数であるので、上記より$E[(Z-c)^2]$を最小にする$c$は$c = E[Z]$であることがわかる。

問題3.11の解答例

$$
\large
\begin{align}
E[(Y – a – b_1X_1 – … – b_nX_n)^2] \qquad &(3.62) \\
a = E[Y] – b_1E[X_1] – … – b_nE[X_n] \quad &(3.63)
\end{align}
$$

上記のように$(3.62)$式、$(3.63)$式が与えられる。ここで$(3.63)$式を$(3.62)$式に代入する。
$$
\large
\begin{align}
& E[(Y – a – b_1X_1 – … – b_nX_n)^2] \\
&= E[(Y -(E[Y] – b_1E[X_1] – … – b_nE[X_n]) – b_1X_1 – … – b_nX_n)^2] \\
&= E[((Y – E[Y]) – b_1(X_1-E[X_1]) – … – b_n(E[X_n]-X_n))^2] \\
&= E[(Y – E[Y])^2] – 2\sum_{i=1}^{n}b_iE[(Y – E[Y])(X_i-E[X_i])] + \sum_{i=1}^{n}\sum_{j=1}^{n}b_ib_jE[(X_i-E[X_i])(X_j-E[X_j])] \\
&= V[Y] – 2\sum_{i=1}^{n}b_i Cov[Y,X_i] + \sum_{i=1}^{n}\sum_{j=1}^{n}b_ib_jCov[X_i,X_j] \quad (1)
\end{align}
$$

上記が$(3.64)$式に一致するので、$(3.64)$式を示すことができる。

次に、下記のように(1)式を$b_i$について偏微分し$0$とおく。
$$
\large
\begin{align}
\frac{\partial}{\partial b_i} \left( V[Y] – 2 \sum_{i=1}^{n}b_i Cov[Y,X_i] + \sum_{i=1}^{n}\sum_{j=1}^{n}b_ib_jCov[X_i,X_j] \right) = 0 \quad (2)
\end{align}
$$

ここで、上記の左辺の第$2$項と第$3$項についてそれぞれ微分を考える。
・第$2$項
$$
\large
\begin{align}
\frac{\partial}{\partial b_i} & \left( – 2 \sum_{i=1}^{n}b_i Cov[Y,X_i] \right) \\
&= -2 \frac{\partial}{\partial b_i} \left( b_1 Cov[Y,X_1] + … + b_i Cov[Y,X_i] + … + b_n Cov[Y,X_n] \right) \\
&= -2 Cov[Y,X_i]
\end{align}
$$

・第$3$項
$$
\large
\begin{align}
\frac{\partial}{\partial b_i} & \left( \sum_{i=1}^{n}\sum_{j=1}^{n}b_ib_jCov[X_i,X_j] \right) \\
&= \frac{\partial}{\partial b_i} \left( b_i^2 Cov[X_i,X_i] + 2 b_i\sum_{j \neq i} Cov[X_i,X_j] + Const \right) \\
&= 2b_i Cov[X_i,X_i] + 2 \sum_{j \neq i} Cov[X_i,X_j] \\
&= 2 \sum_{j=1}^{n} Cov[X_i,X_j]
\end{align}
$$

第$2$項、第$3$項の計算結果を$(2)$式に代入し、下記のように整理を行う。
$$
\large
\begin{align}
\frac{\partial}{\partial b_i} & \left( V[Y] – 2 \sum_{i=1}^{n}b_i Cov[Y,X_i] + \sum_{i=1}^{n}\sum_{j=1}^{n}b_ib_jCov[X_i,X_j] \right) = 0 \\
& -2 Cov[Y,X_i] + 2 \sum_{j=1}^{n} Cov[X_i,X_j] = 0 \\
& Cov[Y,X_i] = \sum_{j=1}^{n} b_jCov[X_i,X_j] \quad (3)
\end{align}
$$

$(3)$式が$(3.65)$式に一致するので、$(3.65)$式を示すことができる。

問題3.12の解答例

$n!$通りの並べ方を考えた上で、左から$y_1, y_2, …, y_n$のようにグループを割り当てていくと考えればよい。

このとき、同一のグループに所属するものの順番は考慮しないので、それぞれ$y_i!$通りの重複が生じる。よって、多項係数は下記のように表すことができる。
$$
\large
\begin{align}
\frac{n!}{y_1!y_2!…y_n!}
\end{align}
$$

また、多項分布の確率$P(Y_1=y_1, …, Y_n=y_n)$は下記のように表すことができる。
$$
\large
\begin{align}
P(Y_1=y_1, …, Y_n=y_n) = \frac{n!}{y_1!y_2!…y_n!} p^{y_1!}…p^{y_n!}
\end{align}
$$

問題3.13の解答例

問題3.14の解答例

$$
\large
\begin{align}
\mathbf{x} &= \left(\begin{array}{c} x_1 \\ … \\ x_n \end{array} \right), \quad \mathbf{\mu} = \left(\begin{array}{c} \mu_1 \\ … \\ \mu_n \end{array} \right) \\
\mathbf{\Sigma} &= \left(\begin{array}{c} \Sigma_{11} & … & \Sigma_{1n} \\ … \\ \Sigma_{n1} & … & \Sigma_{nn} \end{array} \right)
\end{align}
$$
上記のように$\mathbf{x}, \mathbf{\mu}, \mathbf{\Sigma}$を考える際に、多変量正規分布$N(\mathbf{\mu}, \mathbf{\Sigma})$の確率密度関数は下記のように表すことができる。
$$
\large
\begin{align}
f(\mathbf{x}) = \frac{1}{(2 \pi)^{n/2} (det \Sigma)^{1/2}} \exp \left\{ -\frac{1}{2} (\mathbf{x} – \mathbf{\mu})^{T} \Sigma^{-1} (\mathbf{x} – \mathbf{\mu}) \right\}
\end{align}
$$

$$
\large
\begin{align}
\mathbf{X} &= \left(\begin{array}{c} X_1 \\ … \\ X_n \end{array} \right) \\
\mathbf{t} &= \left(\begin{array}{c} t_1 \\ … \\ t_n \end{array} \right)
\end{align}
$$

このとき、上記のように$\mathbf{X}, \mathbf{t}$を定義し、モーメント母関数$m(\mathbf{t}) = E[e^{\mathbf{t}^{T} \mathbf{X}}]$を考える。
$$
\large
\begin{align}
m(\mathbf{t}) &= E \left[ e^{\mathbf{t}^{T} \mathbf{X}} \right] \\
&= \int e^{\mathbf{t}^{T} \mathbf{x}} f(\mathbf{x}) d \mathbf{x} \\
&= \int e^{\mathbf{t}^{T} \mathbf{x}} \times \frac{1}{(2 \pi)^{n/2} (det \Sigma)^{1/2}} \exp \left\{ -\frac{1}{2} (\mathbf{x} – \mathbf{\mu})^{T} \Sigma^{-1} (\mathbf{x} – \mathbf{\mu}) \right\} d \mathbf{x} \\
&= \frac{1}{(2 \pi)^{n/2} (det \Sigma)^{1/2}} \int \exp \left\{ \mathbf{t}^{T} \mathbf{x} – \frac{1}{2} (\mathbf{x} – \mathbf{\mu})^{T} \Sigma^{-1} (\mathbf{x} – \mathbf{\mu}) \right\} d \mathbf{x}
\end{align}
$$

上記の指数関数部分に対し、$\mathbf{x}$に関する平方完成を行うことを考える。
$$
\large
\begin{align}
\mathbf{t}^{T} \mathbf{x} – \frac{1}{2} (\mathbf{x} – \mathbf{\mu})^{T} \Sigma^{-1} (\mathbf{x} – \mathbf{\mu}) &= – \frac{1}{2} (\mathbf{x}^{T} \Sigma^{-1} \mathbf{x} – \mathbf{x}^{T} \Sigma^{-1} \mathbf{\mu} – \mathbf{\mu}^{T} \Sigma^{-1} \mathbf{x} + \mathbf{\mu}^{T} \Sigma^{-1} \mathbf{\mu} – 2 \mathbf{t}^{T} \mathbf{x}) \\
&= \frac{1}{2} (\mathbf{x}^{T} \Sigma^{-1} \mathbf{x} – 2 \mathbf{\mu}^{T} \Sigma^{-1} \mathbf{x} + \mathbf{\mu}^{T} \Sigma^{-1} \mathbf{\mu} – 2 \mathbf{t}^{T} \mathbf{x}) \\
&= – \frac{1}{2} (\mathbf{x}^{T} \Sigma^{-1} \mathbf{x} – 2 (\mathbf{\mu}^{T} \Sigma^{-1} + \mathbf{t}^{T}) \mathbf{x} + \mathbf{\mu}^{T} \Sigma^{-1} \mathbf{\mu}) \\
&= – \frac{1}{2} (\mathbf{x} – \mathbf{\mu} – \Sigma \mathbf{t})^{T} \Sigma^{-1} (\mathbf{x} – \mathbf{\mu} – \Sigma \mathbf{t}) + \mathbf{t}^{T} \mathbf{\mu} + \frac{1}{2} \mathbf{t}^{T} \Sigma^{-1} \mathbf{t}
\end{align}
$$

上記の右辺の$1$項目は積分により消えるため、モーメント母関数の下記が導出できる。
$$
\large
\begin{align}
m(\mathbf{t}) = \exp \left\{ \mathbf{t}^{T} \mathbf{\mu} + \frac{1}{2} \mathbf{t}^{T} \Sigma^{-1} \mathbf{t} \right\}
\end{align}
$$

問題3.15の解答例

$\mathbf{x}, \mathbf{y}, \mathbf{a}$はそれぞれ下記のような$n$次元ベクトルで定義できる。
$$
\large
\begin{align}
\mathbf{x} = \left(\begin{array}{c} x_1 \\ … \\ x_n \end{array} \right), \quad \mathbf{y} = \left(\begin{array}{c} y_1 \\ … \\ y_n \end{array} \right), \quad \mathbf{a} = \left(\begin{array}{c} a_1 \\ … \\ a_n \end{array} \right)
\end{align}
$$

$\mathbf{B}$が$n$次の正則行列であるので、$\mathbf{y} = \mathbf{a} + \mathbf{B}\mathbf{x}$は下記のように変形できる。
$$
\large
\begin{align}
\mathbf{y} &= \mathbf{a} + \mathbf{B}\mathbf{x} \\
\mathbf{B}\mathbf{x} &= \mathbf{y} – \mathbf{a} \\
\mathbf{x} &= \mathbf{B}^{-1} (\mathbf{y} – \mathbf{a})
\end{align}
$$

ここで$\mathbf{B}’ = \mathbf{B}^{-1}$を下記のように定義する。
$$
\large
\begin{align}
\mathbf{B}’ = \left(\begin{array}{c} B’_{11} & … & B’_{1n} \\ … & … & … \\ B’_{n1} & … & B’_{nn} \end{array} \right)
\end{align}
$$
このとき$\mathbf{x} = \mathbf{B}^{-1} (\mathbf{y} – \mathbf{a})$は下記のように表せる。
$$
\large
\begin{align}
\mathbf{x} &= \mathbf{B}^{-1} (\mathbf{y} – \mathbf{a}) \\
\mathbf{x} &= \mathbf{B}’ (\mathbf{y} – \mathbf{a}) \\
\left(\begin{array}{c} x_1 \\ … \\ x_n \end{array} \right) &= \left(\begin{array}{c} B’_{11} & … & B’_{1n} \\ … & … & … \\ B’_{n1} & … & B’_{nn} \end{array} \right) \left(\begin{array}{c} y_1 – a_1 \\ … \\ y_n – a_n \end{array} \right) \\
&= \left(\begin{array}{c} B’_{11}(y_1 – a_1)+…+B’_{1n}(y_n – a_n) \\ … \\ B’_{n1}(y_1 – a_1)+…+B’_{nn}(y_n – a_n) \end{array} \right)
\end{align}
$$

ここで、$J(\partial x / \partial y)$は下記のように計算できる。
$$
\large
\begin{align}
J(\partial x / \partial y) &= \left(\begin{array}{c} \partial x_1 / \partial y_1 & … & \partial x_1 / \partial y_n \\ … & … & … \\ \partial x_n / \partial y_1 & … & \partial x_n / \partial y_n \end{array} \right) \\
&= \left(\begin{array}{c} B’_{11} & … & B’_{1n} \\ … & … & … \\ B’_{n1} & … & B’_{nn} \end{array} \right) \\
&= \mathbf{B}^{-1}
\end{align}
$$

ここまでの議論により$J(\partial x / \partial y) = \mathbf{B}^{-1}$を示すことができる。

問題3.16の解答例

$$
\large
\begin{align}
f_{X,Y|Z}(x,y) = f_{X|Z}(x) f_{Y|Z}(y) \quad (3.18)
\end{align}
$$
上記の$(3.18)$式は条件付き確率の定義に基づいて、下記のように表すことができる。
$$
\large
\begin{align}
f_{X,Y|Z}(x,y) &= f_{X|Z}(x) f_{Y|Z}(y) \\
\frac{f_{X,Y,Z}(x,y,z)}{f_{Z}(z)} &= \frac{f_{X,Z}(x,z)}{f_{Z}(z)} \cdot \frac{f_{Y,Z}(y,z)}{f_{Z}(z)} \quad (1)
\end{align}
$$

ここで$(1)$式の両辺を$\displaystyle \frac{f_{Y,Z}(y,z)}{f_{Z}(z)}$で割ると下記のようになる。
$$
\large
\begin{align}
\frac{f_{X,Y,Z}(x,y,z)}{f_{Z}(z)} \cdot \frac{f_{Z}(z)}{f_{Y,Z}(y,z)} &= \frac{f_{X,Z}(x,z)}{f_{Z}(z)} \\
\frac{f_{X,Y,Z}(x,y,z)}{f_{Y,Z}(y,z)} &= \frac{f_{X,Z}(x,z)}{f_{Z}(z)}
\end{align}
$$
上記は$f_{X|Y,Z}(x) = f_{X|Z}(x)$を意味し、これは$(3.19)$式に一致する。

問題3.17の解答例

「$(3.18)$が成立 $\implies$ $f(x,y,z)=g(x,z)h(y,z)$」と「$f(x,y,z)=g(x,z)h(y,z)$ $\implies$ $(3.18)$が成立」に分けて示す。

・「$(3.18)$が成立 $\implies$ $f(x,y,z)=g(x,z)h(y,z)$」に関して
$$
\large
\begin{align}
f_{X,Y|Z}(x,y) = f_{X|Z}(x) f_{Y|Z}(y) \quad (3.18)
\end{align}
$$

上記の$(3.18)$式は条件付き確率の定義に基づいて、下記のように表すことができる。
$$
\large
\begin{align}
f_{X,Y|Z}(x,y) &= f_{X|Z}(x) f_{Y|Z}(y) \\
\frac{f_{X,Y,Z}(x,y,z)}{f_{Z}(z)} &= \frac{f_{X,Z}(x,z)}{f_{Z}(z)} \cdot \frac{f_{Y,Z}(y,z)}{f_{Z}(z)} \quad (1)
\end{align}
$$

ここで$(1)$式の両辺に$f_{Z}(z)$をかけると下記のようになる。
$$
\large
\begin{align}
\frac{f_{X,Y,Z}(x,y,z)}{f_{Z}(z)} \cdot f_{Z}(z) &= \frac{f_{X,Z}(x,z)}{f_{Z}(z)} \cdot \frac{f_{Y,Z}(y,z)}{f_{Z}(z)} \cdot f_{Z}(z) \\
f_{X,Y,Z}(x,y,z) &= f_{X,Z}(x,z) \cdot \frac{f_{Y,Z}(y,z)}{f_{Z}(z)}
\end{align}
$$
上記において、$\displaystyle g(x,y)=f_{X,Z}(x,z), h(y,z)=\frac{f_{Y,Z}(y,z)}{f_{Z}(z)}$とおくと、$f(x,y,z)=g(x,z)h(y,z)$が成立する。

・「$f(x,y,z)=g(x,z)h(y,z)$ $\implies$ $(3.18)$が成立」に関して
$f(x,y,z)=g(x,z)h(y,z)$のように表せる際に、下記のように$g_{Z}(z), h_{Z}(z)$を定義する。
$$
\large
\begin{align}
g_{Z}(z) &= \int g(x,z) dx \\
h_{Z}(z) &= \int h(y,z) dy
\end{align}
$$

このとき$f(x,y,z)=g(x,z)h(y,z)$より、下記のように表記することもできる。
$$
\large
\begin{align}
f_{X,Z}(x,z) &= g(x,z)h_{Z}(z) \\
f_{Y,Z}(y,z) &= g_{Z}(z)h(y,z) \\
f_{Z}(z) &= g_{Z}(z)h_{Z}(z)
\end{align}
$$

このとき条件付き確率分布の$f_{X,Y|Z}(x,y)$は下記のように表すことができる。
$$
\large
\begin{align}
f_{X,Y|Z}(x,y) &= \frac{f_{X,Y,Z}(x,y,z)}{f_{Z}(z)} \\
&= \frac{g(x,z)h(y,z)}{f_{Z}(z)} \\
&= \frac{f_{X,Z}(x,z)}{h_{Z}(z)} \cdot \frac{f_{Y,Z}(y,z)}{g_{Z}(z)} \cdot
\frac{1}{f_{Z}(z)} \\
&= \frac{f_{X,Z}(x,z)}{f_{Z}(z)} \cdot \frac{f_{Y,Z}(y,z)}{g_{Z}(z)h_{Z}(z)} \\
&= \frac{f_{X,Z}(x,z)}{f_{Z}(z)} \cdot \frac{f_{Y,Z}(y,z)}{f_{Z}(z)} \\
&= f_{X|Z}(x) f_{Y|Z}(y)
\end{align}
$$
上記は$(3.18)$式に一致する。

問題3.18の解答例

$$
\large
\begin{align}
Z_i &= X_iY_i \\
X_i-Z_i &= X_i – X_iY_i \\
&= X_i(1-Y_i) \\
Y_i-Z_i &= Y_i – X_iY_i \\
&= (1-X_i)Y_i \\
1 – X_i – Y_i + Z_i &= 1 – X_i – Y_i + X_iY_i \\
&= (1 – X_i)(1 – Y_i)
\end{align}
$$

上記のように考え、$X_i, Y_i \in \left\{0, 1 \right\}$であることを考慮すると、$(Z_i, X_i-Z_i, Y_i-Z_i, 1-X_i-Y_i+Z_i)$はどれか$1$つのみが$1$でその他が$0$に対応する。これは$4$次元のベルヌーイ試行になる。また、$(Z_i, X_i-Z_i, Y_i-Z_i, 1-X_i-Y_i+Z_i)$のそれぞれの和が$(Z, X-Z, Y-Z, n-X-Y+Z)$に対応するので、これは$4$項分布に従うことを意味する。このとき、確率変数$(Z_i, X_i-Z_i, Y_i-Z_i, 1-X_i-Y_i+Z_i)$の成功確率は$p_1p_2, p_1(1-p_2), (1-p_1)p_2, (1-p_1)(1-p_2)$にそれぞれ対応する。

この$4$項分布の確率関数$P(z,x-z,y-z,n-x-y+z|p_1p_2, p_1(1-p_2), (1-p_1)p_2, (1-p_1)(1-p_2))$は下記のように表すことができる。
$$
\large
\begin{align}
& P(z,x-z,y-z,n-x-y+z|p_1p_2, p_1(1-p_2), (1-p_1)p_2, (1-p_1)(1-p_2)) \\
&= \frac{n!}{z!(x-z)!(y-z)!(n-x-y+z)!} (p_1p_2)^{z} (p_1(1-p_2))^{x-z} ((1-p_1)p_2)^{y-z} ((1-p_1)(1-p_2))^{n-x-y+z} \\
&= \frac{n!}{z!(x-z)!(y-z)!(n-x-y+z)!} p_1^{z+x-z}p_2^{z+y-z}(1-p_1)^{y-z+n-x-y+z}(1-p_2)^{x-z+n-x-y+z} \\
&= \frac{n!}{z!(x-z)!(y-z)!(n-x-y+z)!} p_1^{x}p_2^{y}(1-p_1)^{n-x}(1-p_2)^{n-y}
\end{align}
$$

また、$X, Y$はそれぞれ独立に二項分布に従い、それぞれの確率関数$P(x,n-x|p_1,n), P(y,n-y|p_2,n)$は下記のように表すことができる。
$$
\large
\begin{align}
P(x,n-x|p_1,n) &= \frac{n!}{x!(n-x)!} p_1^{x}(1-p_1)^{n-x} \\
P(y,n-y|p_2,n) &= \frac{n!}{y!(n-y)!} p_1^{y}(1-p_2)^{n-y}
\end{align}
$$

よって、$X, Y$が与えられた際の$Z$の条件付き分布$P(X=x,Y=y|Z=z)$は下記のようになる。
$$
\large
\begin{align}
& P(X=x,Y=y|Z=z) \\
&= \frac{P(z,x-z,y-z,n-x-y+z|p_1p_2, p_1(1-p_2), (1-p_1)p_2, (1-p_1)(1-p_2))}{P(x,n-x|p_1,n)P(y,n-y|p_2,n)} \\
&= \frac{n! p_1^{x}p_2^{y}(1-p_1)^{n-x}(1-p_2)^{n-y}}{z!(x-z)!(y-z)!(n-x-y+z)!} \times \frac{x!(n-x)!}{n! p_1^{x}(1-p_1)^{n-x}} \times \frac{y!(n-y)!}{n! p_2^{y}(1-p_2)^{n-y}} \\
&= \frac{n!}{z!(x-z)!(y-z)!(n-x-y+z)!} \times \frac{x!(n-x)!}{n!} \times \frac{y!(n-y)!}{n!} \\
&= \frac{x!(n-x)!y!(n-y)!}{n!z!(x-z)!(y-z)!(n-x-y+z)!}
\end{align}
$$

・考察
超幾何分布の$N,M,n,k$を解釈すると、「壺に玉が赤玉が$M$個、白玉が$N-M$個の計$N$個入っており、$n$個非復元抽出を行った際の赤玉の個数が$k$個になる際の確率」を考える確率分布である。
これを$(1)$式に置き換えると、「全$n$個のうちの$x$個が赤、$n-x$個が白の際に、$y$個抽出した際に$z$個が赤玉である確率を表す」と考えることができる。
ここで「赤かつ選ばれた場合」を$z$個とカウントしているが、「$Z_i=X_iY_i$は$X_i=1$かつ$Y_i=1$を表す」と考えることで、ここで論じられた$4$項分布と超幾何分布の関連を見て取ることができる。

問題3.19の解答例

$$
\large
\begin{align}
u &= xy \quad (1) \\
v &= \frac{x}{y} \quad (2)
\end{align}
$$

上記に関して逆変換の導出を行う。$(2)$式を変形した$x=vy$を$(1)$式に代入する。
$$
\large
\begin{align}
u &= vy \times y \\
y^2 &= \frac{u}{v} \\
y &= \sqrt{\frac{u}{v}}
\end{align}
$$

上記で得られた$y$を$x=vy$に代入すると下記が得られる。
$$
\large
\begin{align}
x &= vy \\
&= v \sqrt{\frac{u}{v}} \\
&= \sqrt{uv}
\end{align}
$$

よって、下記のような逆変換が得られる。
$$
\large
\begin{align}
x &= \sqrt{uv} \quad (3) \\
y &= \sqrt{\frac{u}{v}} \quad (4)
\end{align}
$$

$(3)$式、$(4)$式で表した逆変換に基づいて、ヤコビ行列$\mathbf{J}$を下記のように考える。
$$
\large
\begin{align}
\mathbf{J} &= \left(\begin{array}{cc} \frac{\partial x}{\partial u} & \frac{\partial x}{\partial v} \\ \frac{\partial y}{\partial u} & \frac{\partial y}{\partial v} \end{array} \right) \\
&= \left(\begin{array}{cc} \frac{\partial}{\partial u} \sqrt{uv} & \frac{\partial}{\partial v} \sqrt{uv} \\ \frac{\partial}{\partial u} \sqrt{\frac{u}{v}} & \frac{\partial}{\partial v} \sqrt{\frac{u}{v}} \end{array} \right) \\
&= \frac{1}{2} \left(\begin{array}{cc} \sqrt{\frac{v}{u}} & \sqrt{\frac{u}{v}} \\ \sqrt{\frac{1}{uv}} & -\sqrt{\frac{u}{v^3}} \end{array} \right) \quad (5)
\end{align}
$$

$(5)$式を元にヤコビアン$|\det \mathbf{J}|$の計算を行う。
$$
\large
\begin{align}
|\det \mathbf{J}| &= \frac{1}{2^2} \left| \sqrt{\frac{v}{u}} \cdot \left( -\sqrt{\frac{u}{v^3}} \right) – \sqrt{\frac{u}{v}} \cdot \sqrt{\frac{1}{uv}} \right| \\
&= \frac{1}{4} \left| -\frac{1}{v} – \frac{1}{v} \right| \\
&= \frac{1}{2v} \quad (6)
\end{align}
$$
$(6)$式の導出にあたっては$x \geq 0, y \geq 0$より$v$が非負であることを前提に絶対値を外した。

次に確率密度関数について考える。$X,Y$に関する確率密度関数の$f(x,y)$は、下記のように表すことができる。
$$
\large
\begin{align}
f(x,y) &= 1, \quad if \quad 0 \leq x \leq 1 \quad and \quad 0 \leq y \leq 1 \\
&= 0, \quad otherwise
\end{align}
$$
$U,V$に関する確率密度関数を$g(u,v)$とすると、$\displaystyle g(u,v) = f(x,y)|\det \mathbf{J}|$が成立する。変換式より$f(x,y)=0$の場合は$g(u,v)=0$であるので、以下は$0 \leq x \leq 1, 0 \leq y \leq 1$に対応する$u,v$の範囲のみを考える。

$0 \leq x \leq 1, 0 \leq y \leq 1$と$(3)$式、$(4)$式より、$u,v$に関して下記の式が成立する。
・$0 \leq x \leq 1$
$$
\large
\begin{align}
0 \leq &\sqrt{uv} \leq 1 \\
0 \leq &uv \leq 1 \\
0 \leq &u \leq \frac{1}{v} \quad (7)
\end{align}
$$
・$0 \leq y \leq 1$
$$
\large
\begin{align}
0 \leq &\sqrt{\frac{u}{v}} \leq 1 \\
0 \leq &\frac{u}{v} \leq 1 \\
0 \leq &u \leq v \quad (8)
\end{align}
$$
不等号の計算にあたっては$v$が非負であることを前提に計算を行った。

$(7)$式、$(8)$式を元に、$0 \leq x \leq 1, 0 \leq y \leq 1$に対応する$u,v$に対して$\displaystyle g(u,v) = f(x,y)|\det \mathbf{J}|$を考える。
$$
\large
\begin{align}
g(u,v) &= f(x,y)|\det \mathbf{J}| \\
&= \frac{1}{2v}, \quad if \quad 0 \leq u \leq \frac{1}{v} \quad and \quad 0 \leq u \leq v \quad (9)
\end{align}
$$

また、$V$に関する周辺密度関数$g(v)$は$(9)$式を$u$に関して積分することで得られる。
$$
\large
\begin{align}
g(v) &= \int_{0}^{\infty} g(u,v) du \\
&= \int_{0}^{\max \{v,1/v\}} \frac{1}{2v} du \\
&= \left[ \frac{u}{2v} \right]_{0}^{\max \{v,1/v\}} \\
&= \frac{1}{2v} \max \{v,1/v\} \\
&= \frac{1}{2} \max \{1,1/v^2\}
\end{align}
$$

・考察
一様分布に関しては式だけではわかりにくいため、以下図示を行う。

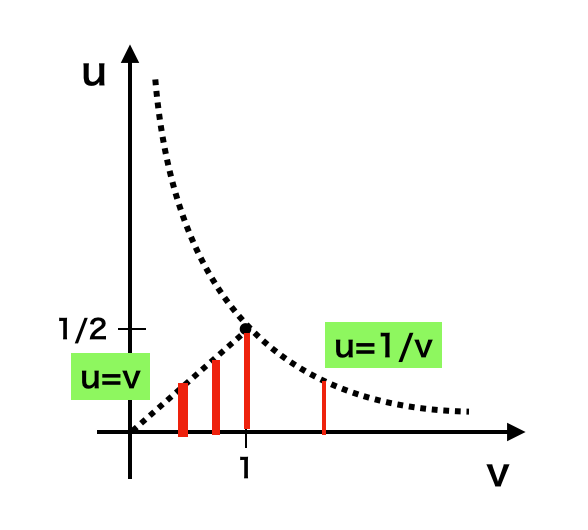
まず$g(u,v)$に関しては、上記のように図示を行った。赤線があるところが確率密度関数の$g(u,v)$が$0$ではない領域を表しており、$v$が$0$に近い方が確率密度関数の値が大きくなることは線の幅で表した。

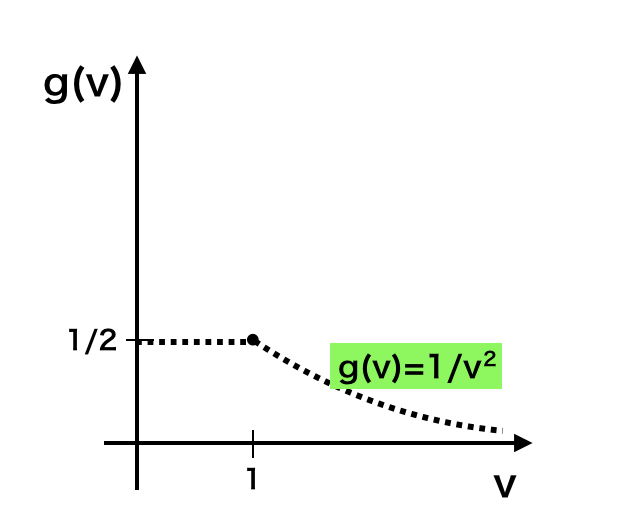
次に周辺密度関数の$g(v)$に関しては上記のように表した。$v \leq 1$では一様分布であり、$v>1$では$1/v^2$に一致することを抑えておくと良いと思われる。

問題3.20の解答例

確率変数$Z$が連続である場合と離散である場合に分けて示す。

・$Z$が連続
$E[|Z-c|]$は確率密度関数の$f(z)$を用いて下記のように表すことができる。
$$
\large
\begin{align}
E[|Z-c|] = \int_{-\infty}^{c} -(x-c) f(x) dx + \int_{c}^{\infty} (x-c) f(x) dx
\end{align}
$$

上記を$c$で微分すると下記のようになる。
$$
\large
\begin{align}
\frac{d E[|Z-c|]}{dc} &= \int_{-\infty}^{c} f(x) dx – \int_{c}^{\infty} f(x) dx \\
&= P(Z \leq c) – P(Z > c)
\end{align}
$$

$c$に関する最小値を考えるので、$\displaystyle \frac{d E[|Z-c|]}{dc} = 0$より、下記が成立する。
$$
\large
\begin{align}
\frac{d E[|Z-c|]}{dc} &= 0 \\
P(Z \leq c) – P(Z > c) &= 0 \\
P(Z \leq c) &= P(Z > c)
\end{align}
$$

確率の定義より$P(Z \leq c) + P(Z > c) = 1$となるので、下記が成立する。
$$
\large
\begin{align}
P(Z \leq c) = P(Z > c) = \frac{1}{2}
\end{align}
$$
上記は$c$がメディアンであることを表すので、$E[|Z-c|]$を最小にする定数$c$は$Z$の分布のメディアンである。

・$Z$が離散
$E[|Z-c|]$は確率関数の$p(z)$を用いて下記のように表すことができる。
$$
\large
\begin{align}
E[|Z-c|] = \sum_{x=-\infty}^{c} -(x-c) p(x) + \sum_{x=c+1}^{\infty} (x-c) p(x)
\end{align}
$$

上記を$c$で微分すると下記のようになる。
$$
\large
\begin{align}
\frac{d E[|Z-c|]}{dc} = \sum_{x=-\infty}^{c} p(x) – \sum_{x=c}^{\infty} p(x) \\
P(Z \leq c) – P(Z > c) &= 0 \\
P(Z \leq c) &= P(Z > c)
\end{align}
$$

上記は連続の場合と同じ式であり、連続の場合と同様に$P(Z \leq c) + P(Z > c) = 1$を用いて、$E[|Z-c|]$を最小にする定数$c$は$Z$の分布のメディアンであることを示すことができる。

問題3.21の解答例