「確率分布」の「変数変換」の仕組みの理解とその応用｜問題演習で理解する統計学【15】

数理統計学における「変数変換」は下記のように、ガウス積分やガンマ分布・ベータ分布に関する議論など、様々なところで出てきます。仕組みの理解も重要な一方で、計算のプロセスに慣れることも重要なので、実践的な演習を通して理解ができるような構成となるよう演習課題の作成を行いました。
https://www.hello-statisticians.com/explain-terms-cat/beta_distribution1.html
https://www.hello-statisticians.com/explain-terms-cat/gaussian_integral1.html

【試験・検定対策用】確率密度関数・確率エレメント・定積分における確率変数の変換の解き方

・標準演習$100$選
https://www.hello-statisticians.com/practice_100

基本問題

変数変換と置換積分

・問題
数理統計学などに出てくる「確率密度関数」の「変数変換」は、「置換積分」と対応づけて理解するとわかりやすい。以下では置換積分に関して確認し、類題的な視点で「確率密度関数」の「変数変換」について確認を行う。
i) 以下の定積分を計算せよ。
$$
\begin{align}
\int_{0}^{2} x dx
\end{align}
$$
ⅱ) i)において、$u=2x$と置き換えるとき、$0 \leq x \leq 2$に対応する$u$の区間と、$\displaystyle \frac{dx}{du}$を求めよ。また、これによってi)の定積分を$u$の「置換積分」を用いて計算せよ。
ⅲ) i)とⅱ)で計算した定積分の結果が一致することについて、直感的に考察せよ。
iv) 区間$[0,2]$における一様分布の確率密度関数を$f(x)$とすると、$f(x)$は下記のように表すことができる。
$$
\begin{align}
f(x) &= \frac{1}{2} \quad (0 \leq x \leq 2) \\
&= 0 \quad (x < 0 , 2 < x)
\end{align}
$$
上記を元に、$\displaystyle \int_{-\infty}^{\infty} f(x) dx$を計算せよ。
v) iv) で計算した一様分布に対して$\displaystyle y = \frac{1}{2}x$となる$y$を考える。この時の$y$の確率密度関数を$g(y)$とするとき、$g(y)$を関数$f$を用いて表せ。また、求めた確率密度関数$g(y)$に対して$\displaystyle \int_{-\infty}^{\infty} g(y) dy$を計算せよ。

・解答

i)
多項式関数の定積分の計算の手順に沿って、下記のように計算することができる。
$$
\large
\begin{align}
\int_{0}^{2} x dx &= \left[ \frac{1}{2}x^2 \right]_{0}^{2} \\
&= \frac{1}{2} (2^2 – 0^2) \\
&= 2
\end{align}
$$

ⅱ)
$u=2x$より、$0 \leq x \leq 2$に対応する$u$の区間は$0 \leq u \leq 4$となる。また、$\displaystyle x = \frac{1}{2}u$より、$\displaystyle \frac{dx}{du}$は下記のように求めることができる。
$$
\large
\begin{align}
\frac{dx}{du} &= \frac{d}{du}\left( \frac{1}{2}u \right) \\
&= \frac{1}{2}
\end{align}
$$
また、この時、$\displaystyle \int_{0}^{2} x dx$に置換積分の考え方を用いることで、下記のように計算することができる。
$$
\large
\begin{align}
\int_{0}^{2} x dx &= \int_{0}^{4} \frac{1}{2}u \frac{dx}{du} du \\
&= \int_{0}^{4} \frac{1}{2}u \cdot \frac{1}{2} du \\
&= \frac{1}{4} \int_{0}^{4} u du \\
&= \frac{1}{4} \left[ \frac{1}{2}x^2 \right]_{0}^{4} \\
&= \frac{1}{8} (4^2 – 0^2) \\
&= 2
\end{align}
$$

ⅲ)
変数$x$を変数$u$で置き換えるにあたって、「積分の区間」を「$0 \leq x \leq 2 \to 0 \leq u \leq 4$」、「変数」を$\displaystyle x \to \frac{1}{2}u$、「積分の微小区間$\displaystyle dx \to \frac{1}{2}du$」のように置き換えを行った。
このことは直感的な視点からは定義域が広くなる一方で、関数の値や微小区間に半減の補正が入ったように考えておくとよいように思われる。

iv)
$\displaystyle \int_{-\infty}^{\infty} f(x) dx$は下記のように計算することができる。
$$
\large
\begin{align}
\int_{-\infty}^{\infty} f(x) dx &= \int_{-\infty}^{0} 0 dx + \int_{0}^{2} \frac{1}{2} dx + \int_{2}^{\infty} 0 dx \\
&= \left[ \frac{x}{2} \right]_{0}^{2} \\
&= \frac{2}{2} = 1
\end{align}
$$

v)
$$
\large
\begin{align}
y &= \frac{1}{2}x \\
x &= 2y \\
\frac{dx}{dy} &= 2
\end{align}
$$
上記と変数変換の式より$g(y)$は$f$を用いて下記のように表すことができる。
$$
\large
\begin{align}
g(y) &= f(x)\frac{dx}{dy} \\
&= f(2y)\frac{dx}{dy} \\
&= 2f(2y)
\end{align}
$$

また、ここで$g(y)=2f(2y)=1$であり、定義域は$0 \leq y \leq 1$である。よって、$\displaystyle \int_{-\infty}^{\infty} g(y) dy$は下記のように計算できる。
$$
\large
\begin{align}
\int_{-\infty}^{\infty} g(y) dy &= \int_{-\infty}^{0} 0 dy + \int_{0}^{1} 1 dy + \int_{1}^{\infty} 0 dy \\
&= \left[ y \right]_{0}^{1} \\
&= 1
\end{align}
$$

・解説
i)とⅱ)で行った置換積分と、iv)とv)で行った変数変換はどちらも積分後の値が同じになるように変形を行う点で同様であると考えて良いと思われます。数理統計学における変数変換は変数変換の公式がメインで取り扱われることが多いですが、このような対応で理解しておくと直感的な理解がしやすいです。

行列式$\det \mathbf{A}$の図形的解釈と平行四辺形の面積

・問題
多次元の変数変換を行うにあたって、前問の$\displaystyle \frac{dx}{dy}$と同様に考えるのがヤコビ行列$\mathbf{J}$やその行列式のヤコビアン$\det \mathbf{J}$である。
https://www.hello-statisticians.com/explain-terms-cat/transformation1.html
上記で取り扱ったようにヤコビ行列$\mathbf{J}$は下記のように表される。
$$
\large
\begin{align}
\mathbf{J} = \left( \begin{array}{cc} \frac{\partial \phi_1^{-1}(y_1,y_2)}{\partial y_1} & \frac{\partial \phi_1^{-1}(y_1,y_2)}{\partial y_2} \\ \frac{\partial \phi_2^{-1}(y_1,y_2)}{\partial y_1} & \frac{\partial \phi_2^{-1}(y_1,y_2)}{\partial y_2} \end{array} \right)
\end{align}
$$
上記に対して行列式の$\det \mathbf{J}$を考えるわけだが、このとき行列式の図形的解釈が理解の前提となるので、以下では行列式の図形的解釈について取り扱う。なお、ヤコビ行列については次問で取り扱う。

行列式の図形的解釈に関連する以下の問いに答えよ。
i) 以下の行列$\mathbf{A}, \mathbf{B}, \mathbf{C}$に対して、それぞれ行列式を求めよ。
$$
\begin{align}
\mathbf{A} = \left( \begin{array}{cc} 3 & 1 \\ 1 & 2 \end{array} \right) \\
\mathbf{B} = \left( \begin{array}{cc} 2 & 1 \\ 1 & 2 \end{array} \right) \\
\mathbf{C} = \left( \begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array} \right)
\end{align}
$$
ⅱ) 下記のように$\mathbf{a}, \mathbf{b}$を定義する。
$$
\begin{align}
\mathbf{a} &= \left( \begin{array}{c} a_1 \\ a_2 \end{array} \right) \\
\mathbf{b} &= \left( \begin{array}{c} b_1 \\ b_2 \end{array} \right)
\end{align}
$$
このとき4点$(0,0), (a_1,a_2), (b_1,b_2), (a_1+b_1,a_2+b_2)$を描画し、平行四辺形を描くことを確認せよ。
ⅲ) ⅱ)で確認した平行四辺形の面積を$S$とするとき、$\displaystyle S=|\mathbf{a}||\mathbf{b}|\sin{\theta}, \mathbf{a} \cdot \mathbf{b}=|\mathbf{a}||\mathbf{b}|\cos{\theta}$が成立することなどを利用して、$S$に関して下記の式が成立することを示せ。
$$
\begin{align}
S = \sqrt{(|\mathbf{a}||\mathbf{b}|)^2-(\mathbf{a} \cdot \mathbf{b})^2}
\end{align}
$$
iv) (3)式に対し、(1)式と(2)式を代入することで、下記が成立することを確認せよ。
$$
\large
\begin{align}
S = a_1b_2 – a_2b_1
\end{align}
$$
v) i)で定義した$\mathbf{A}, \mathbf{B}, \mathbf{C}$に対し、iv)の式を用いてそれぞれ平行四辺形の面積$S$を求めよ。

・解答
i)
$$
\large
\begin{align}
\det \mathbf{A} &= \det \left( \begin{array}{cc} 3 & 1 \\ 1 & 2 \end{array} \right) \\
&= 3 \cdot 2 – 1 \cdot 1 \\
&= 5 \\
\det \mathbf{B} &= \det \left( \begin{array}{cc} 2 & 1 \\ 1 & 2 \end{array} \right) \\
&= 2 \cdot 2 – 1 \cdot 1 \\
&= 3 \\
\det \mathbf{C} &= \det \left( \begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array} \right) \\
&= 1 \cdot 1 – 0 \cdot 0 \\
&= 1
\end{align}
$$

ⅱ)

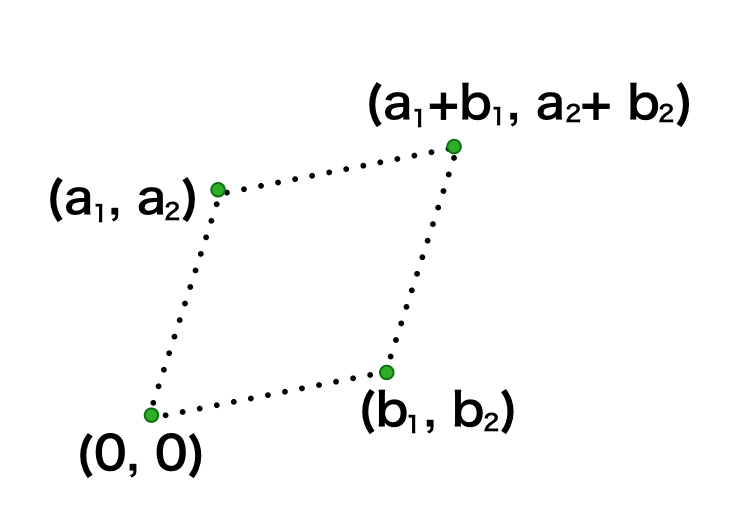
それぞれの点を描画すると上図のようになり、平行四辺形をなすことが確認できる。

ⅲ)
(3)式は下記のように導出できる。
$$
\large
\begin{align}
S &= |\mathbf{a}||\mathbf{b}|\sin{\theta} \\
&= |\mathbf{a}||\mathbf{b}|\sqrt{1-\cos^2{\theta}} \\
&= |\mathbf{a}||\mathbf{b}|\sqrt{1-\frac{(\mathbf{a} \cdot \mathbf{b})^2}{(|\mathbf{a}||\mathbf{b}|)^2}} \\
&= \sqrt{(|\mathbf{a}||\mathbf{b}|)^2-(\mathbf{a} \cdot \mathbf{b})^2}
\end{align}
$$

iv)
$$
\large
\begin{align}
|\mathbf{a}| &= a_1^2+a_2^2 \\
|\mathbf{b}| &= b_1^2+b_2^2 \\
(\mathbf{a} \cdot \mathbf{b})^2 &= (a_1b_1+a_2b_2)^2
\end{align}
$$
上記を(3)式に代入することで下記のように導出できる。
$$
\large
\begin{align}
S &= \sqrt{(|\mathbf{a}||\mathbf{b}|)^2-(\mathbf{a} \cdot \mathbf{b})^2}\\
&= \sqrt{(a_1^2+a_2^2)(b_1^2+b_2^2) – (a_1b_1+a_2b_2)^2} \\
&= \sqrt{a_1^2b_1^2 + a_1^2b_2^2 + a_2^2b_1^2 + a_2^2b_2^2 – (a_1^2b_1^2 + a_2^2b_2^2 – 2a_1a_2b_1b_2)} \\
&= \sqrt{a_1^2b_2^2 + a_2^2b_1^2 – 2a_1a_2b_1b_2} \\
&= \sqrt{(a_1b_2-a_2b_1)^2} \\
&= a_1b_2-a_2b_1 \\
&= \left| \begin{array}{cc} a_1 & a_2 \\ b_1 & b_2 \end{array} \right|
\end{align}
$$

v)
それぞれi)の結果に一致する。

・解説
ⅲ)〜iv)の導出によって、行列式が平行四辺形の面積に一致することが確認できました。ここで得た結果は行列式をヤコビ行列などの様々な場合に適用する場合に役に立つので、このような導出ができることを抑えておくと良いと思います。

ヤコビ行列$\mathbf{J}$とヤコビアン$\det \mathbf{J}$

・問題
2次元のヤコビ行列は下記のように表される。
$$
\large
\begin{align}
\mathbf{J} = \left( \begin{array}{cc} \frac{\partial \phi_1^{-1}(y_1,y_2)}{\partial y_1} & \frac{\partial \phi_1^{-1}(y_1,y_2)}{\partial y_2} \\ \frac{\partial \phi_2^{-1}(y_1,y_2)}{\partial y_1} & \frac{\partial \phi_2^{-1}(y_1,y_2)}{\partial y_2} \end{array} \right)
\end{align}
$$
一般的なヤコビ行列は2次元ではなく$n$次元で定義するが、2次元と$n$次元で取り扱いが大きく異なる訳ではないことから、以下では行列の操作などの計算が比較的行いやすい2次元のヤコビ行列を元に考える。

以下の問いに答えよ。
i) ヤコビ行列に出てくる$\phi_1^{-1}(y_1,y_2)$は$x_1 = \phi_1^{-1}(y_1,y_2)$を表すが、下記のような連立方程式が成立するときの$x_1=\phi_1^{-1}(y_1,y_2), x_2=\phi_2^{-1}(y_1,y_2)$を求めよ。
$$
\large
\begin{align}
y_1 &= 2x_1 + x_2 \\
y_2 &= x_1 + 2x_2
\end{align}
$$
ⅱ) i)で求めた$x_1=\phi_1^{-1}(y_1,y_2), x_2=\phi_2^{-1}(y_1,y_2)$を元に、ヤコビ行列$\mathbf{J}$を求めよ。
ⅲ) $(y_1,y_2), (y_1+dy_1,y_2), (y_1,y_2+dy_2), (y_1+dy_1,y_2+dy_2)$に対してそれぞれ$\phi_1^{-1}, \phi_2^{-1}$を作用させた時にそれぞれの点がどのように変換されるかを求めよ。
iv) $(y_1,y_2), (y_1+dy_1,y_2), (y_1,y_2+dy_2), (y_1+dy_1,y_2+dy_2)$を$(y_1,y_2)$からの位置ベクトルで計算すると、$(0,0), (dy_1,0), (0,dy_2), (dy_1,dy_2)$のようになる。ⅲ)で求めた結果も同様に$(\phi_1^{-1}(y_1,y_2),\phi_2^{-1}(y_1,y_2))$からの位置ベクトルで表せ。
v) $(0,0), (dy_1,0), (0,dy_2), (dy_1,dy_2)$の正方形の面積を$dS$とすると、$dS=dy_1dy_2$となる。iv)で計算した4点の平行四辺形の面積を$dS’$とおいたとき、$dS’$を$dy_1, dy_2$で表せ。ただし、下記で表す前問ⅲ)の式を用いて良い。
$$
\large
\begin{align}
S = \sqrt{(|\mathbf{a}||\mathbf{b}|)^2-(\mathbf{a} \cdot \mathbf{b})^2} \quad (3)
\end{align}
$$
vi) ⅱ)で求めたヤコビ行列$\mathbf{J}$に対して、ヤコビアン$\det \mathbf{J}$を計算せよ。
vⅱ) v)で求めた$dS’$に対して$\displaystyle \frac{dS’}{dS}$を計算すると、vi)で求めた$\det \mathbf{J}$に一致することを確認せよ。

・解答
i)
$$
\large
\begin{align}
y_1 &= 2x_1 + x_2 \\
2y_2 &= 2x_1 + 4x_2
\end{align}
$$
上記の両辺の差を取ることで$x_1$を消去することで、$\displaystyle x_2 = -\frac{1}{3}y_1+\frac{2}{3}y_2$を求めることができる。これを、$x_1=y_2-2x_2$に代入することで、$\displaystyle x_1 = \frac{2}{3}y_1-\frac{1}{3}y_2$を得ることができる。

ここまでの計算により、$x_1=\phi_1^{-1}(y_1,y_2), x_2=\phi_2^{-1}(y_1,y_2)$に関して下記が成立する。
$$
\large
\begin{align}
x_1 &= \phi_1^{-1}(y_1,y_2) = \frac{2}{3}y_1 – \frac{1}{3}y_2 \\
x_2 &= \phi_2^{-1}(y_1,y_2) = -\frac{1}{3}y_1 + \frac{2}{3}y_2
\end{align}
$$

ⅱ)
i)の結果を元に、ヤコビ行列は下記のように計算できる。
$$
\large
\begin{align}
\mathbf{J} &= \left( \begin{array}{cc} \frac{\partial \phi_1^{-1}(y_1,y_2)}{\partial y_1} & \frac{\partial \phi_1^{-1}(y_1,y_2)}{\partial y_2} \\ \frac{\partial \phi_2^{-1}(y_1,y_2)}{\partial y_1} & \frac{\partial \phi_2^{-1}(y_1,y_2)}{\partial y_2} \end{array} \right) \\
&= \left( \begin{array}{cc} \frac{\partial x_1}{\partial y_1} & \frac{\partial x_1}{\partial y_2} \\ \frac{\partial x_2}{\partial y_1} & \frac{\partial x_2}{\partial y_2} \end{array} \right) \\
&= \frac{1}{3} \left( \begin{array}{cc} \frac{\partial}{\partial y_1}(2y_1-y_2) & \frac{\partial}{\partial y_2}(2y_1-y_2) \\ \frac{\partial}{\partial y_1}(-y_1+2y_2) & \frac{\partial}{\partial y_2}(-y_1+2y_2) \end{array} \right) \\
&= \frac{1}{3} \left( \begin{array}{cc} 2 & -1 \\ -1 & 2 \end{array} \right)
\end{align}
$$

ⅲ)
それぞれ下記のように計算できる。
$$
\large
\begin{align}
\left( \begin{array}{c} \phi_1^{-1}(y_1,y_2) \\ \phi_2^{-1}(y_1,y_2) \end{array} \right) &= \frac{1}{3} \left( \begin{array}{c} 2y_1-y_2 \\ -y_1+2y_2 \end{array} \right) \\
\left( \begin{array}{c} \phi_1^{-1}(y_1+dy_1,y_2) \\ \phi_2^{-1}(y_1+dy_1,y_2) \end{array} \right) &= \frac{1}{3} \left( \begin{array}{c} 2(y_1+dy_1)-y_2 \\ -(y_1+dy_1)+2y_2 \end{array} \right) \\
\left( \begin{array}{c} \phi_1^{-1}(y_1,y_2+dy_2) \\ \phi_2^{-1}(y_1,y_2+dy_2) \end{array} \right) &= \frac{1}{3} \left( \begin{array}{c} 2y_1-(y_2+dy_2) \\ -y_1+2(y_2+dy_2) \end{array} \right) \\
\left( \begin{array}{c} \phi_1^{-1}(y_1+dy_1,y_2+dy_2) \\ \phi_2^{-1}(y_1+dy_1,y_2+dy_2) \end{array} \right) &= \frac{1}{3} \left( \begin{array}{c} 2(y_1+dy_1)-(y_2+dy_2) \\ -(y_1+dy_1)+2(y_2+dy_2) \end{array} \right)
\end{align}
$$

iv)
$$
\large
\begin{align}
\phi_1^{-1}(y_1+dy_1,y_2) – \phi_1^{-1}(y_1,y_2) &= \frac{1}{3} (2(y_1+dy_1)-y_2 – (2y_1-y_2)) \\
&= \frac{2}{3}dy_1 \\
\phi_1^{-1}(y_1,y_2+dy_2) – \phi_1^{-1}(y_1,y_2) &= \frac{1}{3} (2y_1-(y_2+dy_2) – (2y_1-y_2)) \\
&= -\frac{1}{3}dy_2 \\
\phi_1^{-1}(y_1+dy_1,y_2+dy_2) – \phi_1^{-1}(y_1,y_2) &= \frac{1}{3} (2(y_1+dy_1)-(y_2+dy_1) – (2y_1-y_2)) \\
&= \frac{2}{3}dy_1-\frac{1}{3}dy_2 \\
\phi_2^{-1}(y_1+dy_1,y_2) – \phi_2^{-1}(y_1,y_2) &= \frac{1}{3} (-(y_1+dy_1)+2y_2 – (-y_1+2y_2)) \\
&= -\frac{1}{3}dy_1 \\
\phi_2^{-1}(y_1,y_2+dy_2) – \phi_2^{-1}(y_1,y_2) &= \frac{1}{3} (-y_1+2(y_2+dy_2) – (-y_1+2y_2)) \\
&= \frac{2}{3}dy_2 \\
\phi_2^{-1}(y_1+dy_1,y_2+dy_2) – \phi_2^{-1}(y_1,y_2) &= \frac{1}{3} (-(y_1+dy_1)+2(y_2+dy_2) – (-y_1+2y_2)) \\
&= -\frac{1}{3}dy_1+\frac{2}{3}dy_2
\end{align}
$$
上記より、位置ベクトルはそれぞれ下記のように計算できる。
$$
\large
\begin{align}
\left( \begin{array}{c} \phi_1^{-1}(y_1,y_2) \\ \phi_2^{-1}(y_1,y_2) \end{array} \right)-\left( \begin{array}{c} \phi_1^{-1}(y_1,y_2) \\ \phi_2^{-1}(y_1,y_2) \end{array} \right) &= \left( \begin{array}{c} 0 \\ 0 \end{array} \right) \\
\left( \begin{array}{c} \phi_1^{-1}(y_1+dy_1,y_2) \\ \phi_2^{-1}(y_1+dy_1,y_2) \end{array} \right)-\left( \begin{array}{c} \phi_1^{-1}(y_1,y_2) \\ \phi_2^{-1}(y_1,y_2) \end{array} \right) &= \frac{1}{3} \left( \begin{array}{c} 2dy_1 \\ -dy_1 \end{array} \right) \\
\left( \begin{array}{c} \phi_1^{-1}(y_1,y_2+dy_2) \\ \phi_2^{-1}(y_1,y_2+dy_2) \end{array} \right)-\left( \begin{array}{c} \phi_1^{-1}(y_1,y_2) \\ \phi_2^{-1}(y_1,y_2) \end{array} \right) &= \frac{1}{3} \left( \begin{array}{c} -dy_2 \\ 2dy_2 \end{array} \right) \\
\left( \begin{array}{c} \phi_1^{-1}(y_1+dy_1,y_2+dy_2) \\ \phi_2^{-1}(y_1+dy_1,y_2+dy_2) \end{array} \right)-\left( \begin{array}{c} \phi_1^{-1}(y_1,y_2) \\ \phi_2^{-1}(y_1,y_2) \end{array} \right) &= \frac{1}{3} \left( \begin{array}{c} 2dy_1-dy_2 \\ -dy_1+2dy_2 \end{array} \right)
\end{align}
$$

v)
面積$dS’$は与えられた式を用いることで下記のように計算できる。
$$
\large
\begin{align}
dS’ &= \sqrt{\frac{5}{9}dy_1^2 \times \frac{5}{9}dy_2^2 – \left( \frac{1}{9}(-2dy_1dy_2 – 2dy_1dy_2) \right)^2} \\
&= \sqrt{ \frac{25}{81}(dy_1dy_2)^2 – \frac{16}{81}(dy_1dy_2)^2 } \\
&= \sqrt{ \frac{9}{81}(dy_1dy_2)^2 } \\
&= \sqrt{ \frac{1}{9}(dy_1dy_2)^2 } \\
&= \frac{1}{3}dy_1dy_2
\end{align}
$$

vi)
ヤコビアン$\det \mathbf{J}$は下記のように計算できる。
$$
\large
\begin{align}
\det \mathbf{J} &= \left| \begin{array}{cc} \frac{2}{3} & -\frac{1}{3} \\ -\frac{1}{3} & \frac{2}{3} \end{array} \right| \\
&= \frac{2}{3} \cdot \frac{2}{3} – \frac{-1}{3} \cdot \frac{-1}{3} \\
&= \frac{1}{3}
\end{align}
$$

vⅱ)
$\displaystyle \frac{dS’}{dS}$は下記のように計算できる。
$$
\large
\begin{align}
\frac{dS’}{dS} &= \frac{\frac{1}{3}dy_1dy_2}{dy_1dy_2} \\
&= \frac{1}{3}
\end{align}
$$
上記はvi)で求めたヤコビアン$\det \mathbf{J}$に一致する。

・解説
ヤコビアンは直感的には面積の変動率と考えることができ、変数変換にあたって微小区間を変更する際に用いられます。v)では前問の解答の$S=a_1b_2-a_1b_2$をそのまま用いる方が計算しやすいですが、少し計算がある方が良いと思われたので、前問における導出前の式を用いました。
ヤコビアンを考えることで$n$次元の変数変換を1次元と同様に考えることができるようになるので、単に公式を抑えるだけでなく、直感的な解釈も同様に身につけておくと良いと思います。

発展問題

ガウス積分

・問題
正規分布の規格化定数の導出などの際に用いられるガウス積分(Gaussian integral)にも変数変換の考え方が用いられている。ガウス積分の基本式は下記のように表される。
$$
\begin{align}
\int_{-\infty}^{\infty} e^{-x^2} dx = \sqrt{\pi}
\end{align}
$$
ガウス積分に関しては上記だけを抑えておくだけで、変数変換から具体的な確率分布に関して導出することができる。以下では変数変換を用いたガウス積分の導出と、標準正規分布の確率密度関数の導出について演習形式で確認を行う。

変数変換を用いたガウス積分の導出にあたって、下記のように積分値を$I$と$I^2$を考える。
$$
\begin{align}
I &= \int_{-\infty}^{\infty} e^{-x^2} dx \quad (1) \\
I^2 &= \left(\int_{-\infty}^{\infty} e^{-x^2} dx\right)^2 \\
&= \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} e^{-x^2} e^{-y^2} dx dy \\
&= \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} e^{-(x^2+y^2)} dx dy \quad (2)
\end{align}
$$

ここまでの内容を元に、下記の問いに答えよ。
i) $x = r \cos{\theta}, y = r \sin{\theta}$のようにおくとき、$x^2+y^2$を計算せよ。
ⅱ) i)で設定を行った$r, \theta$に関して、下記のヤコビ行列$\mathbf{J}$を計算せよ。
$$
\begin{align}
\mathbf{J} &= \left( \begin{array}{cc} \frac{\partial x}{\partial r} & \frac{\partial x}{\partial \theta} \\ \frac{\partial y}{\partial r} & \frac{\partial y}{\partial \theta} \end{array} \right)
\end{align}
$$
ⅲ) ⅱ)で計算したヤコビ行列$\mathbf{J}$に関して、ヤコビアン$|\det \mathbf{J}|$を計算せよ。
iv) $-\infty < x < \infty, -\infty < y < \infty$に対応する、$r$と$\theta$の区間を求めよ。
v) i)〜iv)の結果を元に、(2)式を$r$と$\theta$に関する定積分の式に直し、$I^2$の値を求めよ。ただし下記の計算が成立することを利用してよい。
$$
\begin{align}
\int_{0}^{\infty} r e^{-r^2} dr &= \int_{0}^{\infty} r e^{-r^2} dr \\
&= \left[ -\frac{1}{2}e^{-r^2} \right]_{0}^{\infty} \\
&= \frac{1}{2}
\end{align}
$$
vi) 標準正規分布の確率密度関数を$\displaystyle f(x) = C e^{-\frac{x^2}{2}}$のようにおき、$\displaystyle t = \frac{x}{\sqrt{2}}$を用いて変数変換を行うことを考える。
$$
\begin{align}
\int_{-\infty}^{\infty} C e^{-\frac{x^2}{2}} dx &= 1 \\
\int_{-\infty}^{\infty} e^{-t^2} dx &= \sqrt{\pi}
\end{align}
$$
上記が成立することを利用し、$C$の値を求めよ。
vⅱ) vi)で導出した確率密度関数の式に対して、$y = \mu + \sigma x$を用いて変数変換を行うことを考える。このとき$y$に関する確率密度関数を$g(y)$とおくとき、$g(y)$を導出せよ。

・解答
i)
$x^2+y^2$は下記のように計算できる。
$$
\large
\begin{align}
x^2+y^2 &= r^2 \cos^2{\theta} + r^2 \sin^2{\theta} \\
&= r^2 ( \cos^2{\theta} + \sin^2{\theta} ) \\
&= r^2
\end{align}
$$

ⅱ)
ヤコビ行列$\mathbf{J}$は下記のように計算できる。
$$
\large
\begin{align}
\mathbf{J} &= \left( \begin{array}{cc} \frac{\partial x}{\partial r} & \frac{\partial x}{\partial \theta} \\ \frac{\partial y}{\partial r} & \frac{\partial y}{\partial \theta} \end{array} \right) \\
&= \left( \begin{array}{cc} \frac{\partial}{\partial r}(r \cos{\theta}) & \frac{\partial}{\partial \theta}(r \cos{\theta}) \\ \frac{\partial}{\partial r}(r \sin{\theta}) & \frac{\partial}{\partial \theta}(r \sin{\theta}) \end{array} \right) \\
&= \left( \begin{array}{cc} \cos{\theta} & -r \sin{\theta} \\ \sin{\theta} & r \cos{\theta} \end{array} \right)
\end{align}
$$

ⅲ)
ヤコビアン$|\det \mathbf{J}|$は下記のように計算できる。
$$
\large
\begin{align}
|\det \mathbf{J}| &= \left| \begin{array}{cc} \cos{\theta} & -r \sin{\theta} \\ \sin{\theta} & r \cos{\theta} \end{array} \right| \\
&= \cos{\theta} \cdot r \cos{\theta} – (-r \sin{\theta}) \cdot \sin{\theta} \\
&= r(\cos^2{\theta}+\sin^2{\theta}) \\
&= r
\end{align}
$$

iv)
$0 < r < \infty, 0 \leq \theta \leq 2 \pi$を考えることで、$-\infty < x < \infty, -\infty < y < \infty$に対応させることができる。

v)
下記のように計算を行うことができる。
$$
\large
\begin{align}
I^2 &= \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} e^{-(x^2+y^2)} dx dy \\
&= \int_{0}^{2 \pi} \int_{0}^{\infty} e^{-r^2} |\det \mathbf{J}| dr d \theta \\
&= \int_{0}^{2 \pi} \int_{0}^{\infty} re^{-r^2} dr d \theta \\
&= 2 \pi \int_{0}^{\infty} re^{-r^2} dr \\
&= 2 \pi \left[ -\frac{1}{2}e^{-r^2} \right]_{0}^{\infty} \\
&= \frac{2 \pi}{2} \\
&= \pi
\end{align}
$$

vi)
変数変換後の$t$に関する確率密度関数を$f_1(t)$とおくと、$\displaystyle f_1(t)=f(x)\left| \frac{dx}{dt} \right|, x = \sqrt{2}t$より、$f_1(t)$は下記のように計算できる。
$$
\large
\begin{align}
f_1(t) &= f(x)\left| \frac{dx}{dt} \right| \\
&= f(\sqrt{2}t) \times \sqrt{2} \\
&= \sqrt{2} C e^{-\frac{(\sqrt{2}t)^2}{2}} \\
&= \sqrt{2} C e^{-\frac{(2t^2}{2}} \\
&= \sqrt{2} C e^{-t^2}
\end{align}
$$

ここで$f_1(t)$の全区間に対して積分を考える。
$$
\large
\begin{align}
\int_{-\infty}^{\infty} f_1(t) dt &= \int_{-\infty}^{\infty} \sqrt{2} C e^{-t^2} dt \\
&= \sqrt{2} C \int_{-\infty}^{\infty} e^{-t^2} dt \\
&= \sqrt{2 \pi} C
\end{align}
$$
上記の計算にあたって与えられたガウス積分の式を用いた。

ここで$\displaystyle \int_{-\infty}^{\infty} f_1(t) dt = \int_{-\infty}^{\infty} C e^{-\frac{x^2}{2}} dx = 1$より、$\sqrt{2 \pi} C = 1$が成立する。よって、$C$は下記であることがわかる。
$$
\large
\begin{align}
\sqrt{2 \pi} C &= 1 \\
C &= \frac{1}{\sqrt{2 \pi}}
\end{align}
$$

vⅱ)
https://www.hello-statisticians.com/practice/stat_practice1.html#i-6
上記のv)と同様に、$g(y)$は下記のように導出される。
$$
\large
\begin{align}
g(y) &= f(x) \left| \frac{dx}{dy} \right| \\
&= f \left( \frac{y-\mu}{\sigma} \right) \left| \frac{d}{dy} \left( \frac{y-\mu}{\sigma} \right) \right| \\
&= \frac{1}{\sqrt{2 \pi}} \exp \left( -\frac{(y-\mu / \sigma)^2}{2} \right) \times \frac{1}{\sigma} \\
&= \frac{1}{\sqrt{2 \pi \sigma^2}} \exp \left( -\frac{(y-\mu)^2}{2 \sigma^2} \right)
\end{align}
$$

・解説
i)〜v)より$I^2=\pi$が得られ、これよりガウス積分に関する$\displaystyle \int_{-\infty}^{\infty} e^{-x^2} dx = \sqrt{\pi}$が成立することが確認できます。また、vi)とvⅱ)によって、標準正規分布$N(0,1)$や正規分布$N(\mu,\sigma^2)$の確率密度関数を導出することができます。このように変数変換を用いることでガウス積分が導出でき、正規分布の確率密度関数における定数項の導出に役立てることができます。

下記のガウス積分についての記事も合わせて参考にしてみてください。
https://www.hello-statisticians.com/explain-terms-cat/gaussian_integral1.html

ガンマ分布とベータ分布

下記で取り扱った。
https://www.hello-statisticians.com/practice/stat_practice_basic5.html#i-9

変数変換による標本分布の確率密度関数の導出

・問題
標本を表す確率変数$X_1,X_2,…,X_n$に対する標本の関数を$T=T(X_1,X_2,…,X_n)$のようにおくとき、$T$は統計量と定義される。「統計量」は難しい印象があるかもしれないが、単に「標本の関数」と考えればそれほど難しくない。

統計量の具体例に関しては、下記のように標本平均や標本分散を考えることができる。
$$
\large
\begin{align}
\bar{X} &= \frac{1}{n} \sum_{i=1}^{n} X_i \\
S^2 &= \frac{1}{n} \sum_{i=1}^{n} (X_i – \bar{X})^2
\end{align}
$$

さて、このように統計量を定義することができるが、この統計量の確率分布は「標本分布」と言われる。標本分布の具体例は「正規分布」、「$\chi^2$分布」、「$t$分布」、「$F$分布」などがあるが、以下では「$t$分布」を例に変数変換を用いた確率密度関数の導出を行う。

これまでの内容を元に以下の問いに答えよ。
i) $X_1,X_2,…,X_n$に関する不偏標本分散を$s^2$とおくとき、$s^2$を式で表せ。
ⅱ) 「$X_1,X_2,…,X_n \sim N(\mu,\sigma^2), i.i.d.$」とするとき、$t$統計量$T$を答えよ。
ⅲ) ⅱ)で表した$t$統計量$T$を変形し、下記を導出せよ。
$$
\large
\begin{align}
T = \frac{\frac{(\bar{X}-\mu)}{\sigma/\sqrt{n}}}{\sqrt{\frac{s^2}{\sigma^2}}} \quad (1)
\end{align}
$$
iv) $(1)$式の分子はどのような分布に従うか答えよ。
v) $U,V$が互いに独立かつ、$U \sim N(0,1), V \sim \chi^2(m)$が成立するとき、下記で定義する$T$が自由度$m$の$t$分布$t(m)$に従う。
$$
\begin{align}
T = \frac{U}{\sqrt{V/m}} \quad (2)
\end{align}
$$
$(1)$式に対して、$\displaystyle U=\frac{(\bar{X}-\mu)}{\sigma/\sqrt{n}}, V=\frac{(n-1)s^2}{\sigma^2}$を用いて変数を置き換えよ。また、導出結果を$(2)$式と見比べることで$m$を$n$を用いて表し、これが何を表すか解釈せよ。
vi) $U \sim N(0,1), V \sim \chi^2(m)$の同時確率密度関数$f(u,v)$は下記のように表される。
$$
\large
\begin{align}
f(u,v) = \frac{1}{\sqrt{2 \pi}} e^{-\frac{u^2}{2}} \frac{v^{\frac{m}{2}-1} e^{-\frac{v}{2}}}{2^{\frac{m}{2}} \Gamma \left( \frac{m}{2} \right)}
\end{align}
$$
ここで$(2)$式を元に$\displaystyle T = \frac{U}{\sqrt{V/m}}, V=V$のような変数変換を行うとき、$U$を$T$で表し、ヤコビ行列$\mathbf{J}$、ヤコビアン$|\det \mathbf{J}|$を計算せよ。
vⅱ) $(3)$式に対して$\displaystyle T = \frac{U}{\sqrt{V/m}}, V=V$のような変数変換を行った際の確率密度関数を$g(t,v)$とおくとき、$g(t,v)$は下記に一致することを確認せよ。
$$
\large
\begin{align}
g(t,v) = \frac{v^{\frac{m+1}{2}-1} e^{-v \left( 1 + \frac{t^2}{2m} \right)}}{2^{\frac{m}{2}} \Gamma \left( \frac{m}{2} \right) \sqrt{2 \pi m}}
\end{align}
$$

・解答
i)
不偏標本分散$s^2$は下記のように表すことができる。
$$
\large
\begin{align}
s^2 = \frac{1}{n-1} \sum_{i=1}^{n} (X_i-\bar{X})^2
\end{align}
$$

ⅱ)
$t$統計量$T$は下記のように表すことができる。
$$
\large
\begin{align}
T = \frac{\sqrt{n}(\bar{X}-\mu)}{s}
\end{align}
$$

ⅲ)
ⅱ)の結果を元に下記のように変形を行うことで導出することができる。
$$
\large
\begin{align}
T &= \frac{\sqrt{n}(\bar{X}-\mu)}{s} \\
&= \frac{\sqrt{n}(\bar{X}-\mu)/\sigma}{s/\sigma} \\
&= \frac{\frac{(\bar{X}-\mu)}{\sigma/\sqrt{n}}}{\sqrt{\frac{s^2}{\sigma^2}}}
\end{align}
$$
分子と分母に$1/\sigma$をかけ合わせることで導出できる。

iv)
標準正規分布$N(0,1)$に従う。

v)
下記のように変数の置き換えを行うことができる。
$$
\large
\begin{align}
T &= \frac{\frac{(\bar{X}-\mu)}{\sigma/\sqrt{n}}}{\sqrt{\frac{s^2}{\sigma^2}}} \\
&= \frac{\frac{(\bar{X}-\mu)}{\sigma/\sqrt{n}}}{\sqrt{\frac{(n-1)s^2}{\sigma^2}/(n-1)}} \\
&= \frac{U}{\sqrt{V/(n-1)}}
\end{align}
$$
上記を$(2)$式を見比べると$m=n-1$であり、これより$t$統計量が自由度$n-1$の$t$分布$t(n-1)$に従うと解釈することができる。

vi)
ヤコビ行列$\mathbf{J}$は下記のように計算できる。
$$
\large
\begin{align}
\mathbf{J} &= \left(\begin{array}{cc} \frac{\partial u}{\partial t} & \frac{\partial u}{\partial v} \\ \frac{\partial v}{\partial t} & \frac{\partial v}{\partial v} \end{array} \right) \\
&= \left(\begin{array}{cc} \sqrt{\frac{v}{m}} & \frac{t}{2}\sqrt{\frac{1}{mv}} \\ 0 & 1 \end{array} \right)
\end{align}
$$
上記を元にヤコビアン$|\det \mathbf{J}|$は下記のように計算できる。
$$
\large
\begin{align}
|\det \mathbf{J}| &= \left| \sqrt{\frac{v}{m}} \cdot 1 – \frac{t}{2}\sqrt{\frac{1}{mv}} \cdot 0 \right| \\
&= \sqrt{\frac{v}{m}}
\end{align}
$$

vⅱ)
$g(t,v)$は下記のように導出することができる。
$$
\large
\begin{align}
g(t,v) &= f(u,v) |\det \mathbf{J}| \\
&= f \left( t \sqrt{\frac{v}{m}} , v \right) |\det \mathbf{J}| \\
&= \frac{1}{\sqrt{2 \pi}} e^{-\frac{\left( t \sqrt{\frac{v}{m}} \right)^2}{2}} \times \frac{v^{\frac{m}{2}-1} e^{-\frac{v}{2}}}{2^{\frac{m}{2}} \Gamma \left( \frac{m}{2} \right)} \times \sqrt{\frac{v}{m}} \\
&= \frac{1}{\sqrt{2 \pi}} e^{-v\frac{t^2}{2m}} \times \frac{v^{\frac{m}{2}-1} e^{-\frac{v}{2}}}{2^{\frac{m}{2}} \Gamma \left( \frac{m}{2} \right)} \times \sqrt{\frac{v}{m}} \\
&= \frac{v^{\frac{m+1}{2}-1} e^{-v \left( 1 + \frac{t^2}{2m} \right)}}{2^{\frac{m}{2}} \Gamma \left( \frac{m}{2} \right) \sqrt{2 \pi m}}
\end{align}
$$

・解説
i)〜v)では$n$個の確率変数に基づく$t$統計量が自由度$n-1$の$t$分布$t(n-1)$に従うことについて確認を行いました。
vi)とvⅱ)で$t$分布の確率密度関数の導出にあたっての変数変換について取り扱いました。ここでは取り扱いませんでしたが、vⅱ)式で$v$を積分消去することで$t$分布の確率密度関数$f(t)$は下記のようになります。
$$
\large
\begin{align}
f(t) &= \int_{0}^{\infty} g(t,v) dv \\
&= \frac{\Gamma \left( \frac{m+1}{2} \right)}{\sqrt{\pi m} \Gamma \left( \frac{m}{2} \right)} \left( 1 + \frac{t^2}{m} \right)^{-\frac{m+1}{2}}
\end{align}
$$
上記に関しては下記で詳しい導出を取り扱いました。
https://www.hello-statisticians.com/explain-terms-cat/sampling_distribution1.html#t-2

確率密度関数の畳み込み

累積分布関数の変数変換

・問題
確率密度関数の変数変換を行う際はヤコビアンなどを含む公式に基づいて基本的には導出を行うことができる。一方で、自由度$1$の$\chi^2$分布の確率密度関数の導出の際に標準正規分布$\mathcal{N}(0,1)$に関して$Y=X^2$の変数変換を考える場合などは確率密度関数を元に考えると区間の表示が難しい。

このような際は累積分布関数の変数変換を考えると置換積分の考え方に基づいてシンプルに導出を行える。以下、累積分布関数の置換積分に関して確認を行う。下記の問いにそれぞれ答えよ。

i) 標準正規分布$\mathcal{N}(0,1)$の確率密度関数を$f_1(x)$、累積分布関数$F_1(x)$とおくとき、$f_1(x), F_1(x)$を$x$の式で表せ。
ⅱ) i)で取り扱った変数$x$に対応する確率変数$X$に対して変数変換$Y=X^2$を考える。この際、$P(Y \leq u)$を$P(0 \leq X \leq \sqrt{u})$を用いて表せ。
ⅲ) 自由度$1$の$\chi^2$分布の確率密度関数を$f_2(y)$、累積分布関数を$F_2(y)$のようにおくとき、$\displaystyle P(0 \leq X \leq \sqrt{u}) = \int_{0}^{\sqrt{u}} f_1(x) dx$であることに基づいて、$F_2(u) = P(Y \leq u)$を導出せよ。
iv) ⅲ)の導出結果より自由度$1$の$\chi^2$分布の確率密度関数$f_2(y)$を$y$の式で表せ。
v) 自由度$1$の$\chi^2$分布がガンマ分布$\displaystyle \mathrm{Ga} \left( \frac{1}{2},2 \right)$に一致することを確認せよ。
vi) 変数変換$Y=X^2$を考える際に累積分布関数を考える利点に関して論じよ。

・解答
i)
$f_1(x), F_1(x)$はそれぞれ下記のように表せる。
$$
\large
\begin{align}
f_1(x) &= \frac{1}{\sqrt{2 \pi}} \exp{ \left( -\frac{x^2}{2} \right) } \\
F_1(x) &= \int_{-\infty}^{x} f_1(t) dt \\
&= \frac{1}{\sqrt{2 \pi}} \int_{-\infty}^{x} \exp{ \left( -\frac{t^2}{2} \right) } dt
\end{align}
$$

ⅱ)
$Y \leq u$は$-\sqrt{u} \leq X \leq \sqrt{u}$に対応する。標準正規分布は$x=0$に対称な偶関数であるので、$P(Y \leq u) = 2P(0 \leq X \leq \sqrt{u})$のように表すことができる。

ⅲ)
$P(Y \leq u) = 2P(0 \leq X \leq \sqrt{u})$や$\displaystyle P(0 \leq X \leq \sqrt{u}) = \int_{0}^{\sqrt{u}} f_1(x) dx$より、$F_2(u) = P(Y \leq u)$は下記のように表せる。
$$
\large
\begin{align}
F_2(u) &= P(Y \leq u) = 2P(0 \leq X \leq \sqrt{u}) \\
&= 2 \int_{0}^{\sqrt{u}} f_1(x) dx \quad (1)
\end{align}
$$

上記に対して$y=x^2$のように変数変換を考える。$x \geq 0$であれば$\displaystyle x = \sqrt{y}, dx = \frac{1}{2 \sqrt{y}}$が成立する。また、$x$と$y$の区間は下記のように対応する。

$x$	$0 \to u$
$y$	$0 \to \sqrt{u}$

よって$(1)$式は下記のように変形できる。
$$
\large
\begin{align}
F_2(u) &= P(Y \leq u) = 2P(0 \leq X \leq \sqrt{u}) \\
&= 2 \int_{0}^{\sqrt{u}} f_1(x) dx \quad (1) \\
&= 2 \int_{0}^{u} f_2(\sqrt{y}) \cdot \frac{1}{2 \sqrt{y}} dy \\
&= \cancel{2} \int_{0}^{u} \frac{1}{\sqrt{2 \pi}} \exp{ \left( -\frac{y}{2} \right) } \cdot \frac{1}{\cancel{2} \sqrt{y}} dy \\
&= \int_{0}^{u} \frac{1}{\sqrt{2 \pi y}} \exp{ \left( -\frac{y}{2} \right) } dy
\end{align}
$$

iv)
ⅲ)の導出結果より、$f_2(y)$は下記のように表せる。
$$
\large
\begin{align}
f_2(y) = \frac{1}{\sqrt{2 \pi y}} \exp{ \left( -\frac{y}{2} \right) }
\end{align}
$$

v)
ガンマ分布$\mathrm{Ga}(\alpha,\beta)$の確率密度関数を$f(x)$とおくと$f(x)$は下記のように表せる。
$$
\large
\begin{align}
f(x) = \frac{1}{\beta^{\alpha} \Gamma(\alpha)} y^{\alpha-1} \exp{ \left( -\frac{y}{\beta} \right) }
\end{align}
$$

パラメータの対応を考えることにより、自由度$1$の$\chi^2$分布がガンマ分布$\displaystyle\mathrm{Ga} \left( \frac{1}{2},2 \right)$に一致することが確認できる。

vi)
$Y=X^2$は$Y=aX+b$のような$1$対$1$対応の変換ではないので、$X<0$の場合と$X<0$の場合に分けて考察する必要が生じるが、この取り扱いを数式展開で表すことはなかなか複雑であり難しい。一方で累積分布関数を考える場合は関数の対称性などを用いて式の取り扱いがしやすい。

・解説
この問題で取り扱ったように「確率密度関数の変数変換」と「累積分布関数の変数変換」は対応するので、基本的には変数変換が$1$対$1$対応の場合は確率密度関数、$1$対$1$でない場合は累積分布関数を用いると良いと思います。