統計学を学ぶにあたって、グラフなどを用いて視覚的に理解することは重要です。PythonではMatplotlibがシンプルで使いやすいですが、毎度調べるというのは大変です。そこで当記事ではMatplotlibの抑えておきたい用法について一問一答形式でまとめました。
配列には主にNumPyを用いますので、NumPyの使い方に関してはわからなければ適宜調べるようにお願いします。また、実行結果の図示に関しては容量の都合上省略しているものも多いです。
基本事項の確認
配列の定義
下記のように配列の定義は行う。
import numpy as np
x = np.arange(0., 2.1, 0.1)
y = 2.*x + 1.
print(x)
print(y)・実行結果
> print(x)
[ 0. 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1. 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2. ]
> print(y)
[ 1. 1.2 1.4 1.6 1.8 2. 2.2 2.4 2.6 2.8 3. 3.2 3.4 3.6 3.8 4. 4.2 4.4 4.6 4.8 5. ]配列xの定義にあたっては、numpy.arangeやnp.linspaceを用いることで作成を行える。また、np.arrayなどを用いて多次元リストを変換する場合もある。以下ではグラフの作成の際のxやyに関して先に与え、出題という形式でまとめる。
ライブラリの読み込み
解答$1$つ$1$つでライブラリの読み込みを行うと冗長であるので、以下を実行した上でそれぞれの解答のプログラムを実行する必要がある。
import numpy as np
import matplotlib.pyplot as plt
from scipy import statspyplotの用法
グラフの描画
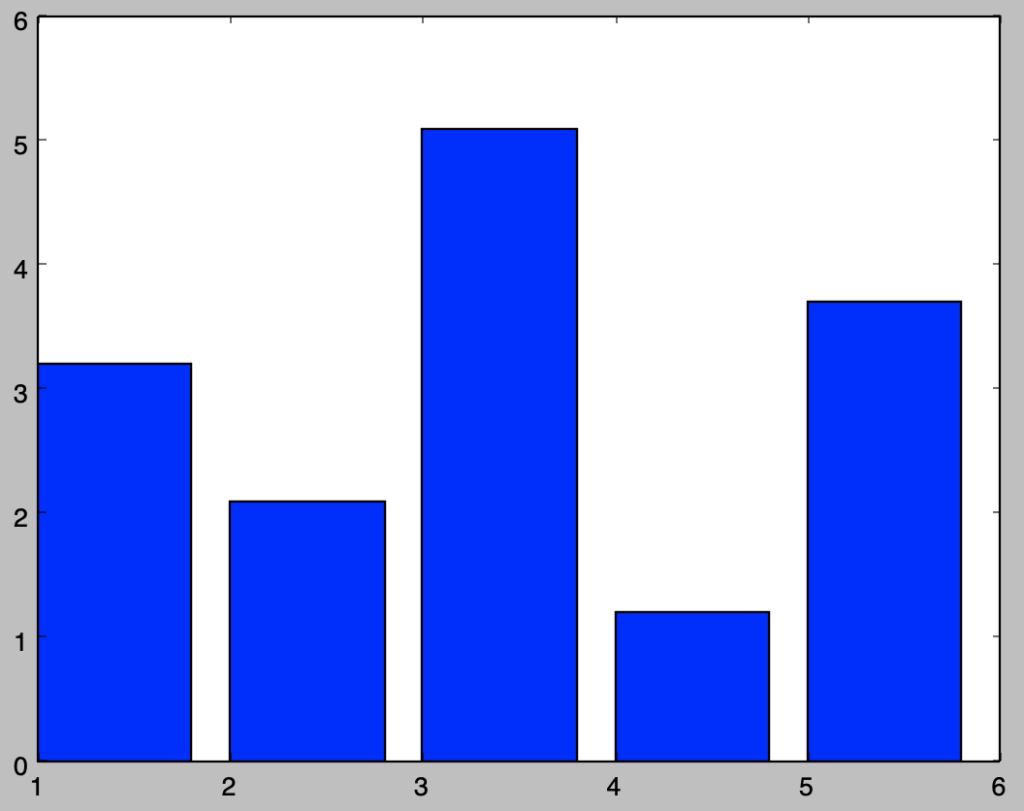
Q.1-1-1 棒グラフの描画
x = np.array([1,2,3,4,5])
y = np.array([3.2, 2.1, 5.1, 1.2, 3.7])上記のように与えられたxとyに対して棒グラフの描画を行え。
・解答
plt.bar(x,y)
plt.show()・実行結果
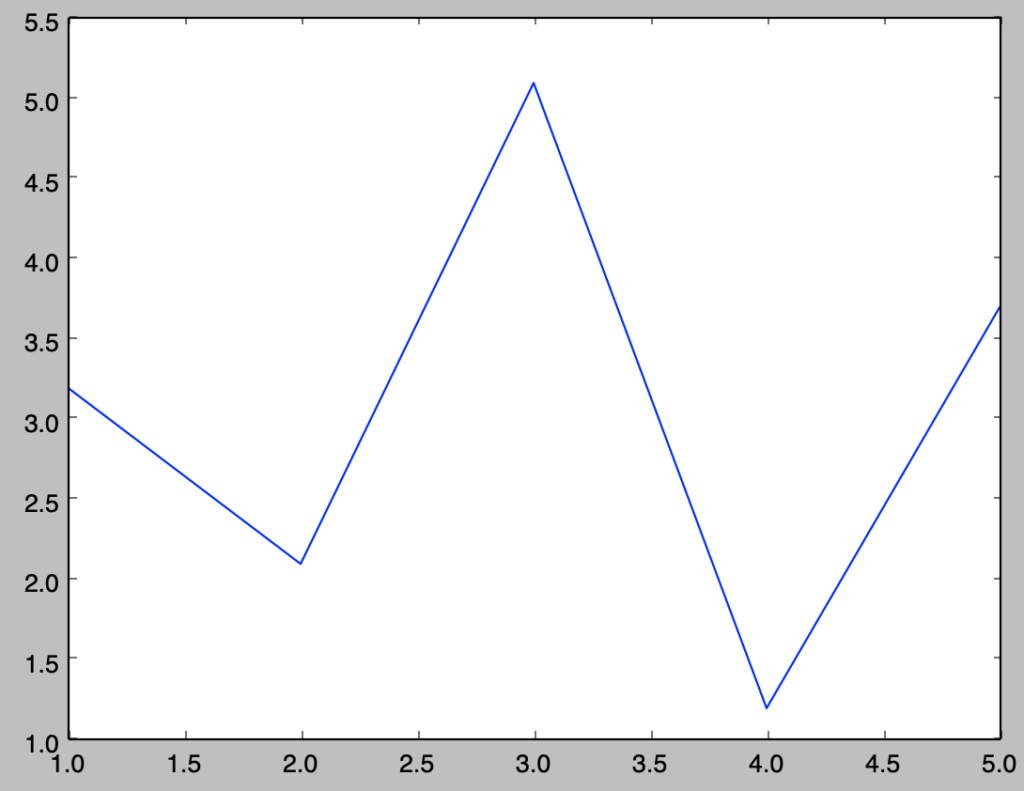
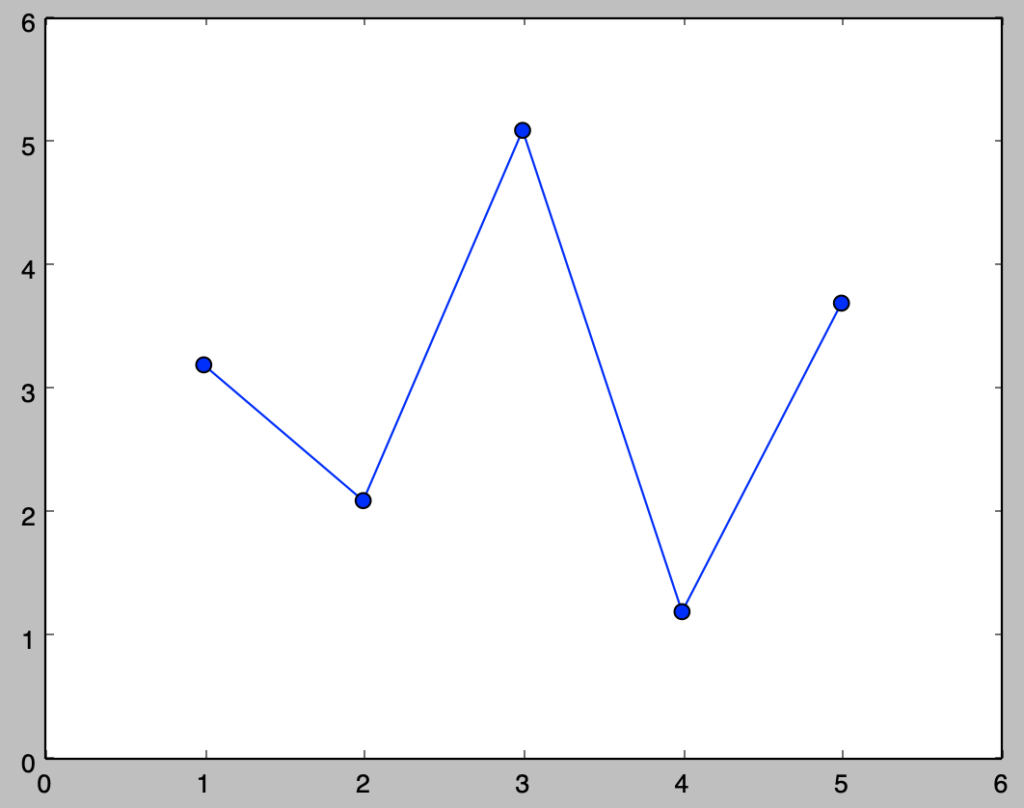
Q.1-1-2 折れ線グラフの描画
x = np.array([1,2,3,4,5])
y = np.array([3.2, 2.1, 5.1, 1.2, 3.7])上記のように与えられたxとyに対して折れ線グラフの描画を行え。
・解答
plt.plot(x,y)
plt.show()・実行結果
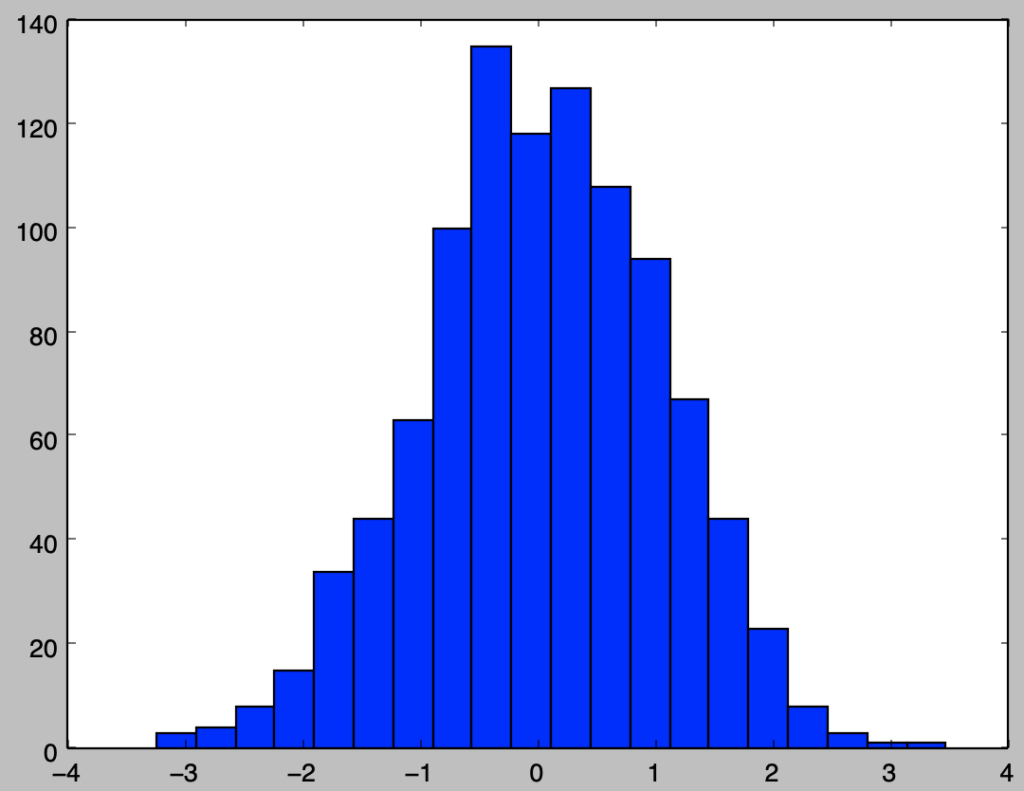
Q.1-1-3 ヒストグラムの描画
x = stats.norm.rvs(size=1000)上記のように与えられたxに対して区間の数が$20$個のヒストグラムの描画を行え。
・解答
plt.hist(x,bins=20)
plt.show()・実行結果
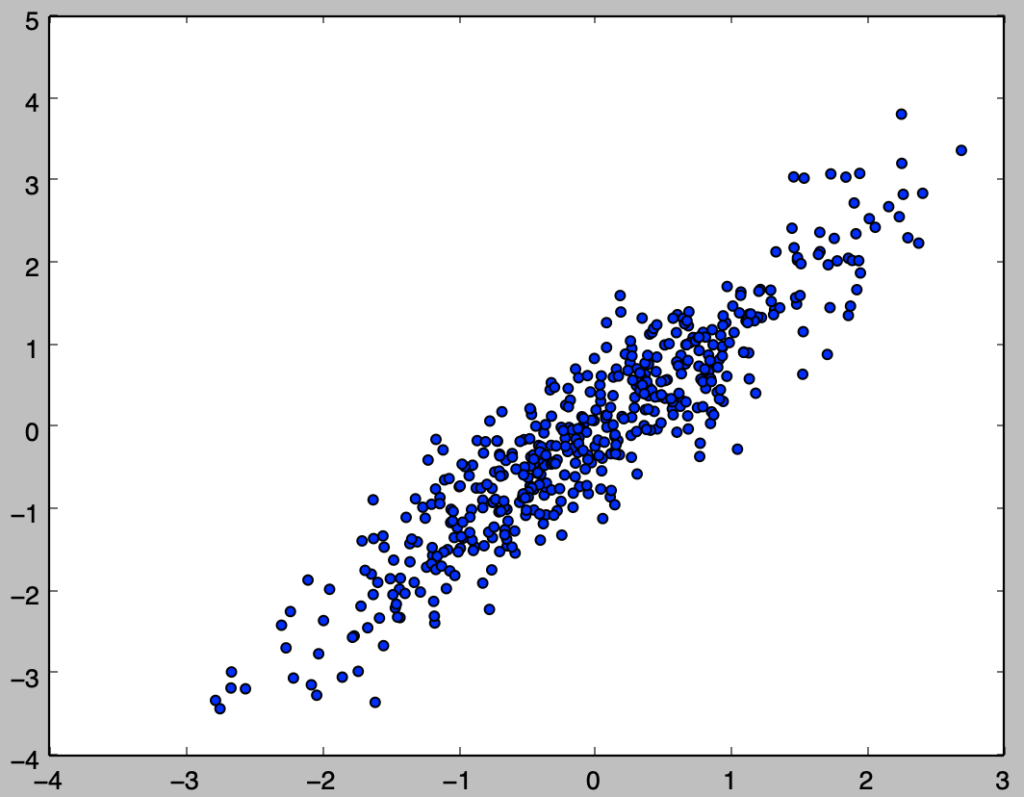
Q.1-1-4 散布図の描画
np.random.seed(0)
x = stats.norm.rvs(size=500)
y = 1.2*x + 0.5*stats.norm.rvs(size=500)上記のように与えられたxとyに対して散布図の描画を行え。
・解答
plt.scatter(x,y)
plt.show()・実行結果
Q.1-1-5 plt.plotを用いた円の描画
$x^2 + y^2 = 1$の描画をplt.plotを用いて行え。
・解答
pi = np.linspace(0,2*np.pi,100)
x = np.cos(pi)
y = np.sin(pi)
plt.plot(x,y)
plt.show()・実行結果
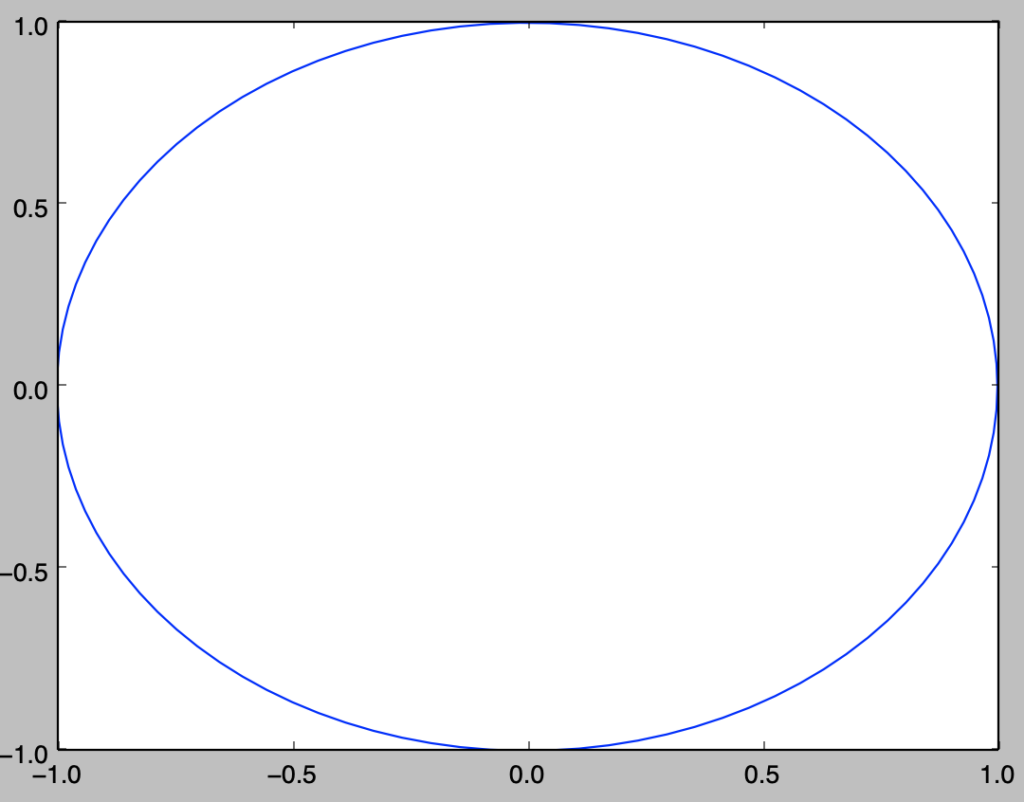
Q.1-1-6 plt.fill_betweenを用いた領域の描画
plt.fill_betweenを用いて$0 \leq x \leq 1, x^2 \leq y \leq x$の領域を図示せよ。
・解答
x = np.arange(0., 1.01, 0.01)
y1 = x**2
y2 = x
plt.fill_between(x, y1, y2, alpha=0.3)
plt.show()・実行結果
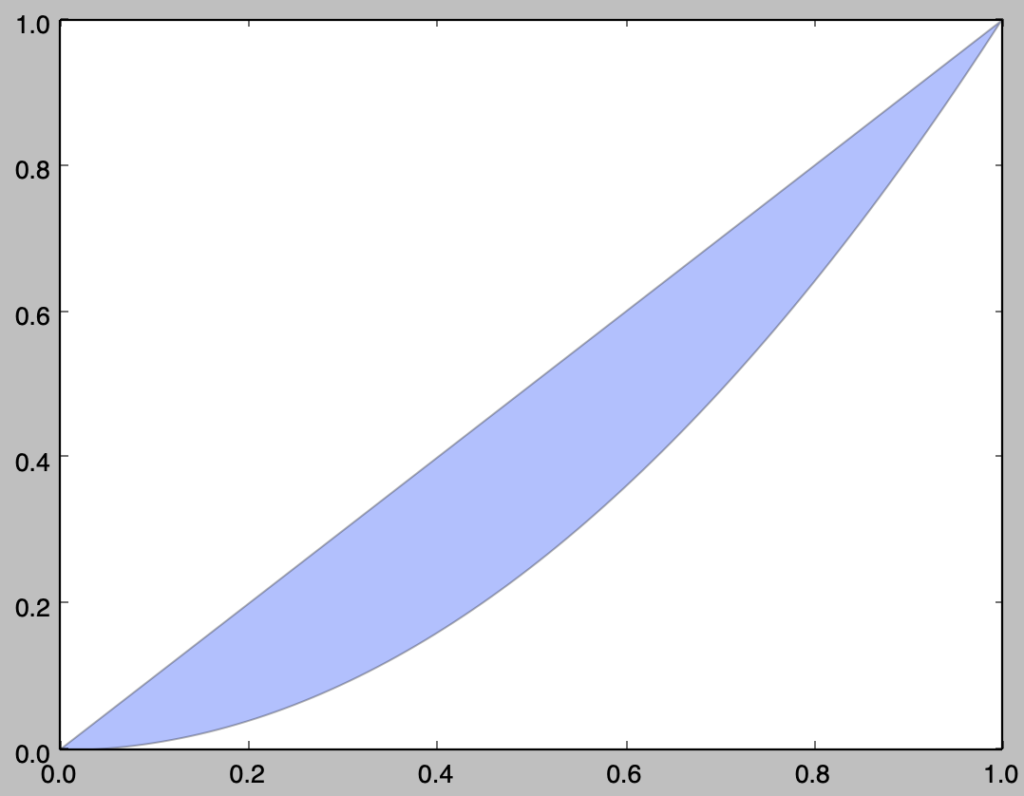
plt.fill_betweenは区間推定を行う際などに用いることが多いが、alpha=0.3のように指定することで区間と推定値の双方を見やすく表示できることは抑えておくと良い。
Q.1-1-7 plt.hist2dを用いた$2$次元ヒストグラムの描画
np.random.seed(0)
n = 100000
U1, U2 = np.random.rand(n), np.random.rand(n)
X = np.sqrt(-2*np.log(U1)) * np.cos(2*np.pi*U2)
Y = np.sqrt(-2*np.log(U1)) * np.sin(2*np.pi*U2)上記を実行することでボックスミュラー法に基づいて正規乱数XとYの生成を行なうことができる。plt.hist2dを用いてXとYを$2$次元ヒストグラムの形式で描画せよ。
・解答
plt.hist2d(X,Y,bins=50)
plt.show()・実行結果
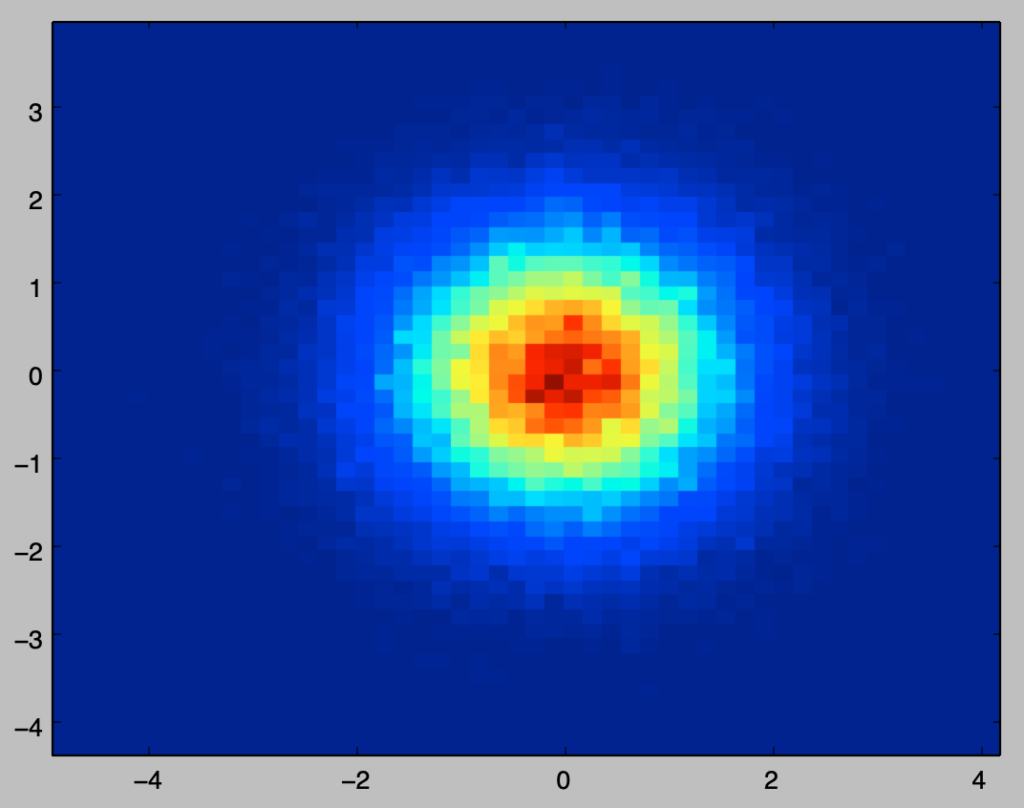
・参考
ボックスミュラー法
グラフの調整
Q.1-2-1 グラフの色
Q.$1$-$3$で取り扱ったヒストグラムを緑で表せ。
・解答
np.random.seed(0)
x = stats.norm.rvs(size=1000)
plt.hist(x,bins=20,color="green")
plt.show()・実行結果
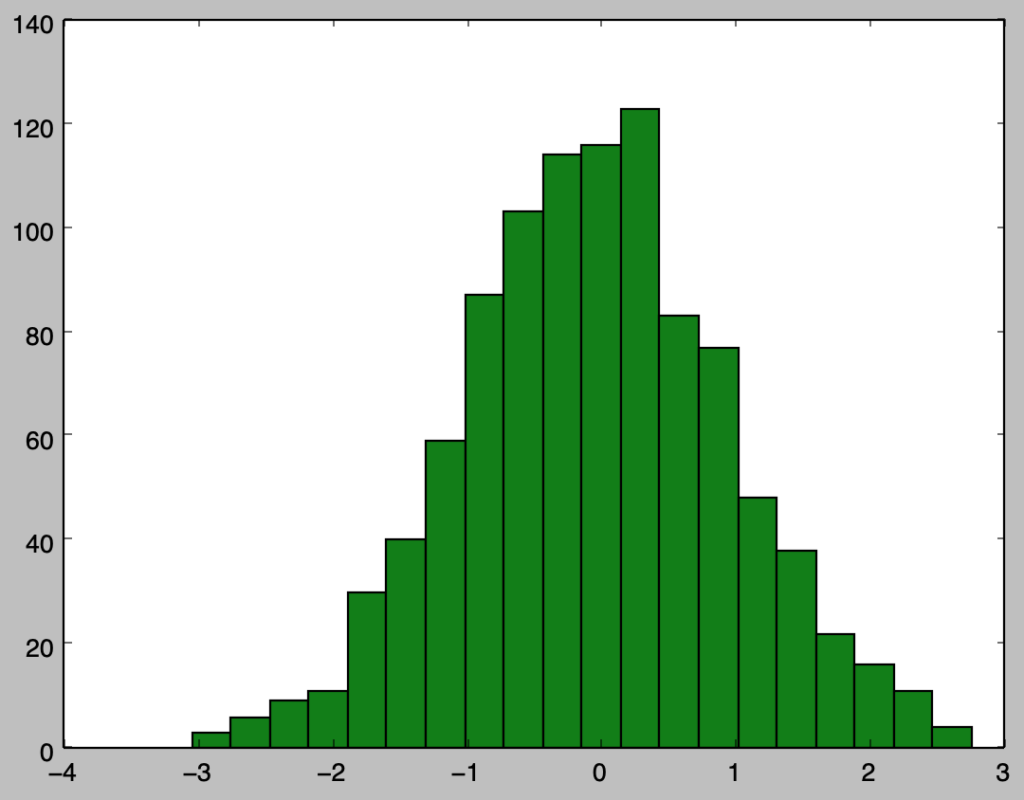
以下、グラフの色の使い分けに関しては見やすさを重視し、特に指定なく使用する。
Q.1-2-2 範囲の調整
Q.$1$-$1$-$5$の描画結果を$-1.2 \leq x \leq 1.2, -1.2 \leq y \leq 1.2$で表せ。
・解答
pi = np.linspace(0,2*np.pi,100)
x = np.cos(pi)
y = np.sin(pi)
plt.plot(x,y)
plt.xlim([-1.2,1.2])
plt.ylim([-1.2,1.2])
plt.show()・実行結果
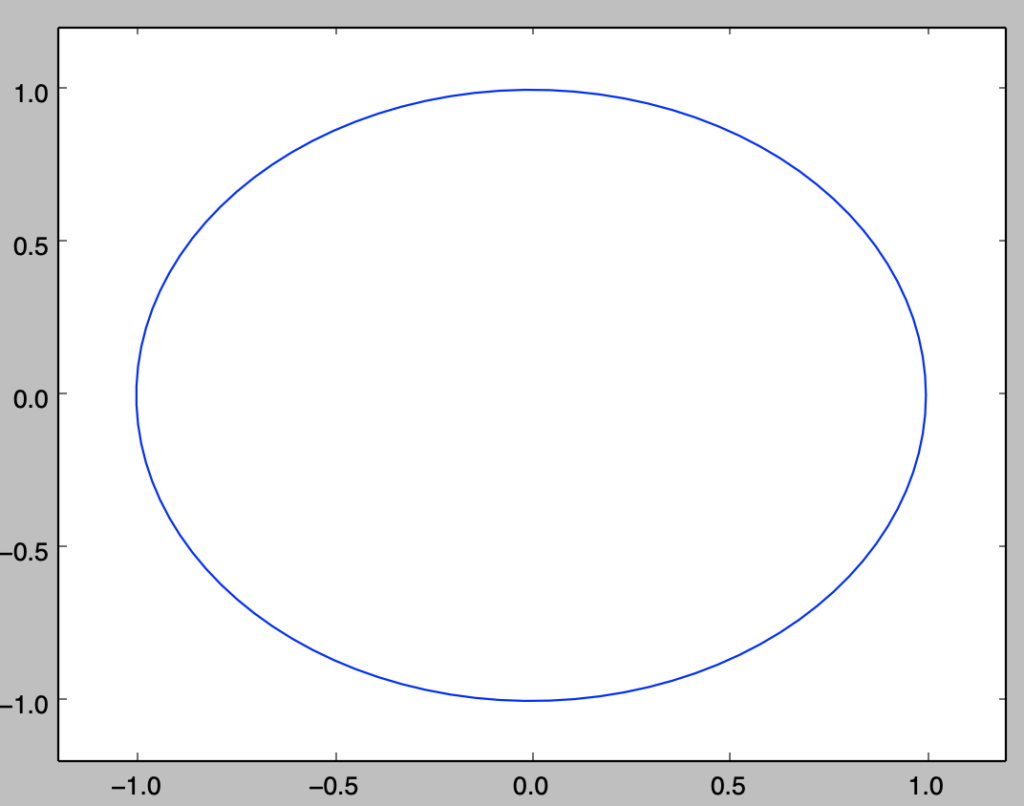
Q.1-2-3 凡例の追加
x = np.arange(0.,5.1,0.1)
y1 = 2*x + 1
y2 = x**2y1とy2に関してグラフを作成し、それぞれ凡例を示せ。
・解答
plt.plot(x,y1,label="y1")
plt.plot(x,y2,label="y2")
plt.legend()
plt.show()・実行結果
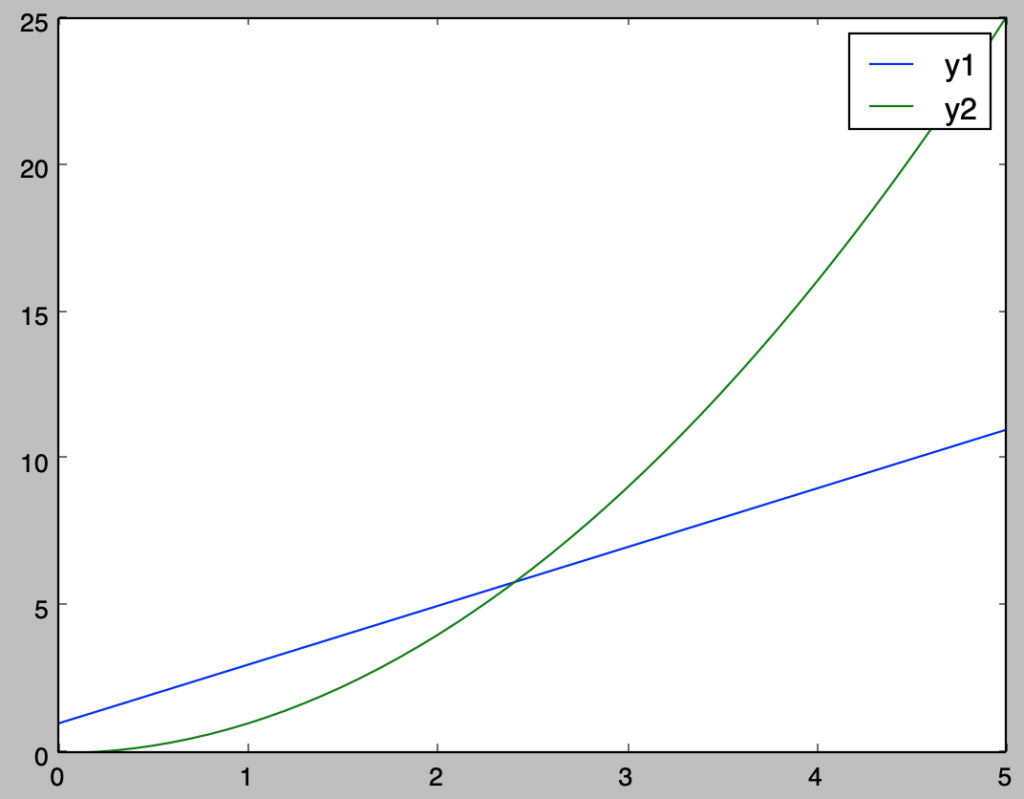
Q.1-2-4 凡例の位置の調整
Q.$1$-$2$-$3$の凡例を左上に配置せよ。
・解答
plt.plot(x,y1,label="y1")
plt.plot(x,y2,label="y2")
plt.legend(loc="upper left")
plt.show()・実行結果
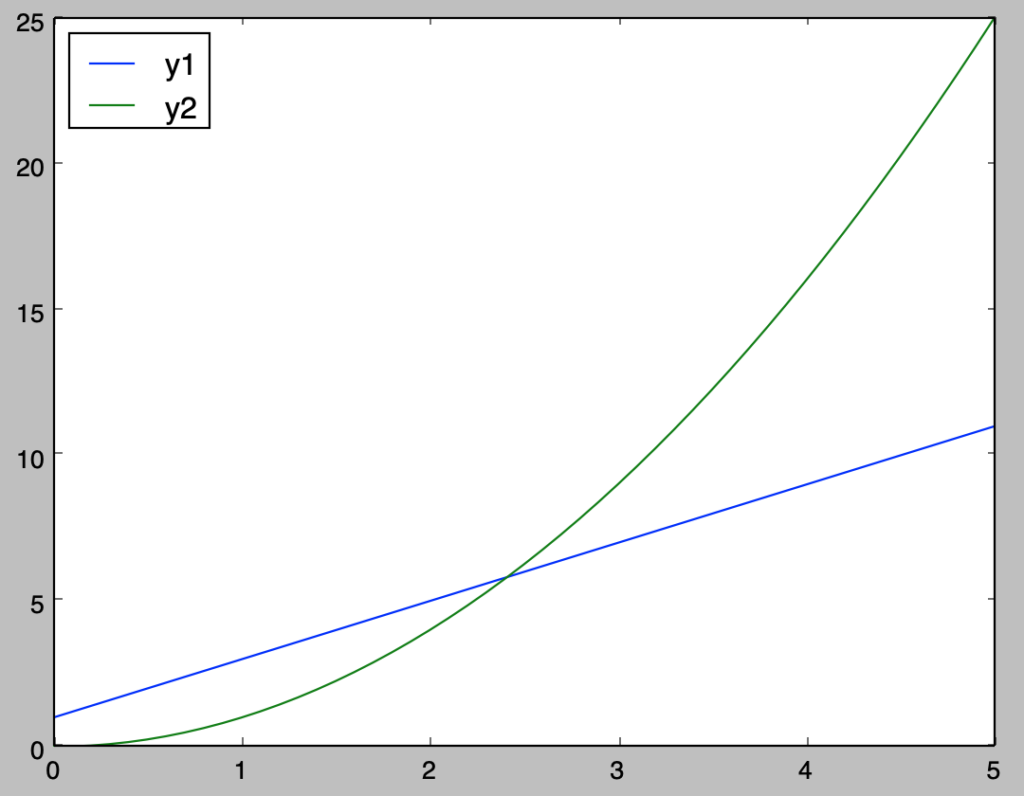
Q.1-2-5 図のタイトルの追加
np.random.seed(0)
x = stats.norm.rvs(size=1000)Q.$1$-$1$-$3$と同様に上記のヒストグラムを作成し、タイトルに「Histgram」を追加せよ。
・解答
plt.hist(x,bins=20)
plt.title("Histgram")
plt.show()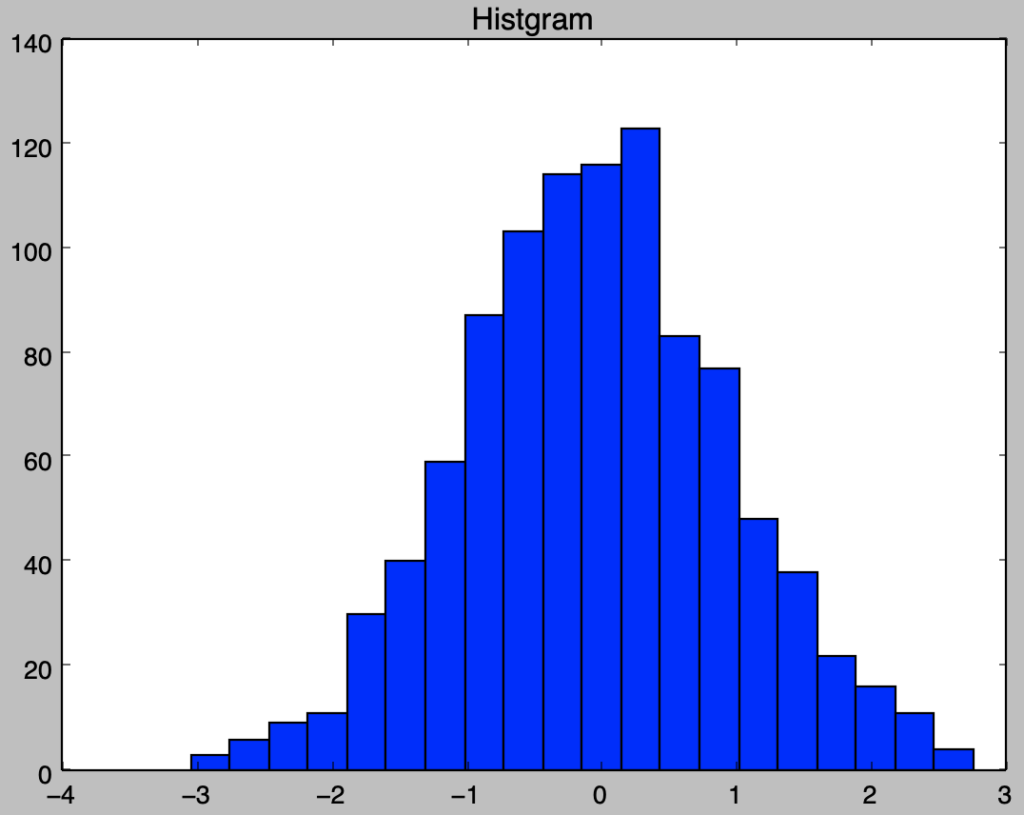
Q.1-2-6 常用対数グラフの作成
x = np.arange(0.1,5.1,0.1)
y1 = 2*x + 1
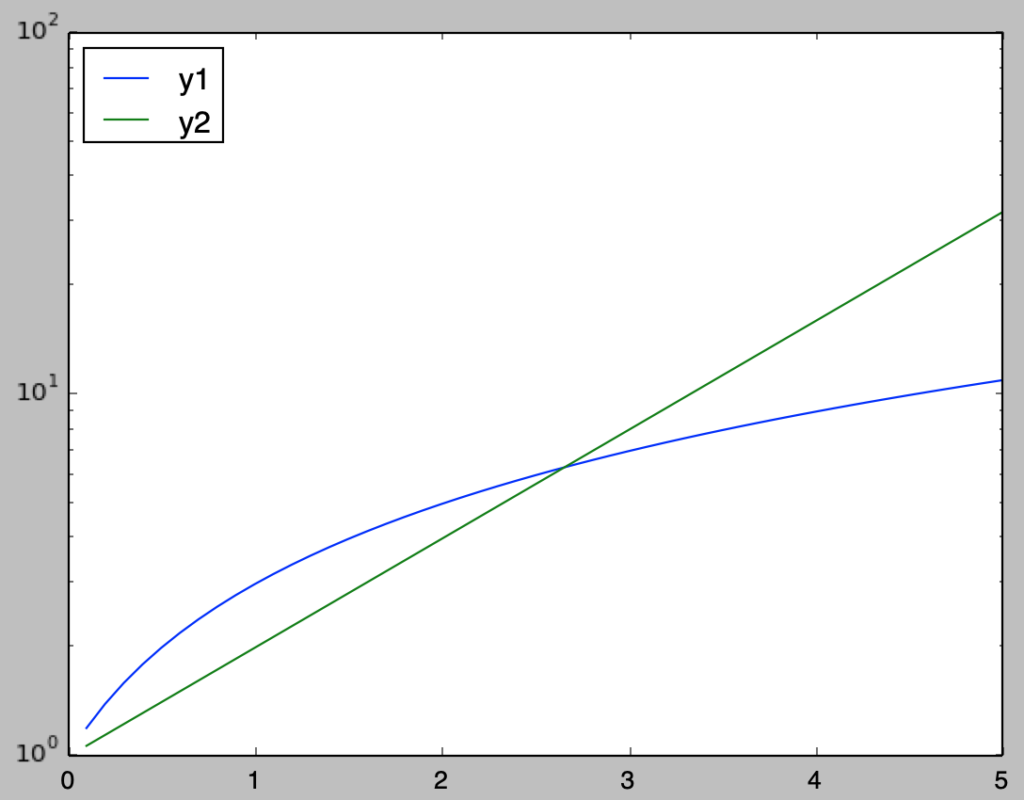
y2 = 2**x上記のy1とy2を常用対数のスケールでグラフ化せよ。
・解答
plt.plot(x,y1,label="y1")
plt.plot(x,y2,label="y2")
plt.yscale("log")
plt.legend(loc="upper left")
plt.show()・実行結果
Q.1-2-7 対数グラフの底の変換
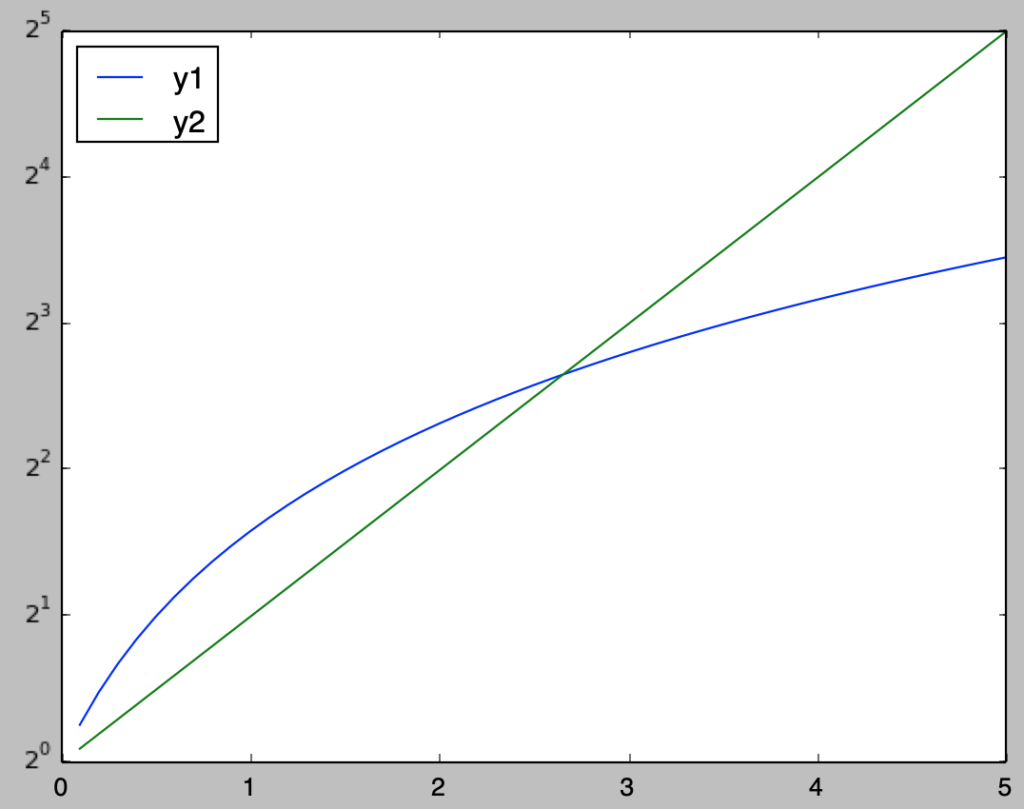
Q.$1$-$2$-$6$を対数の底を$2$に設定し、グラフの作成を行え。
・解答
plt.plot(x,y1,label="y1")
plt.plot(x,y2,label="y2")
plt.yscale("log", basey=2)
plt.legend(loc="upper left")
plt.show()・実行結果
Q.1-2-8 マーカーの形と大きさ
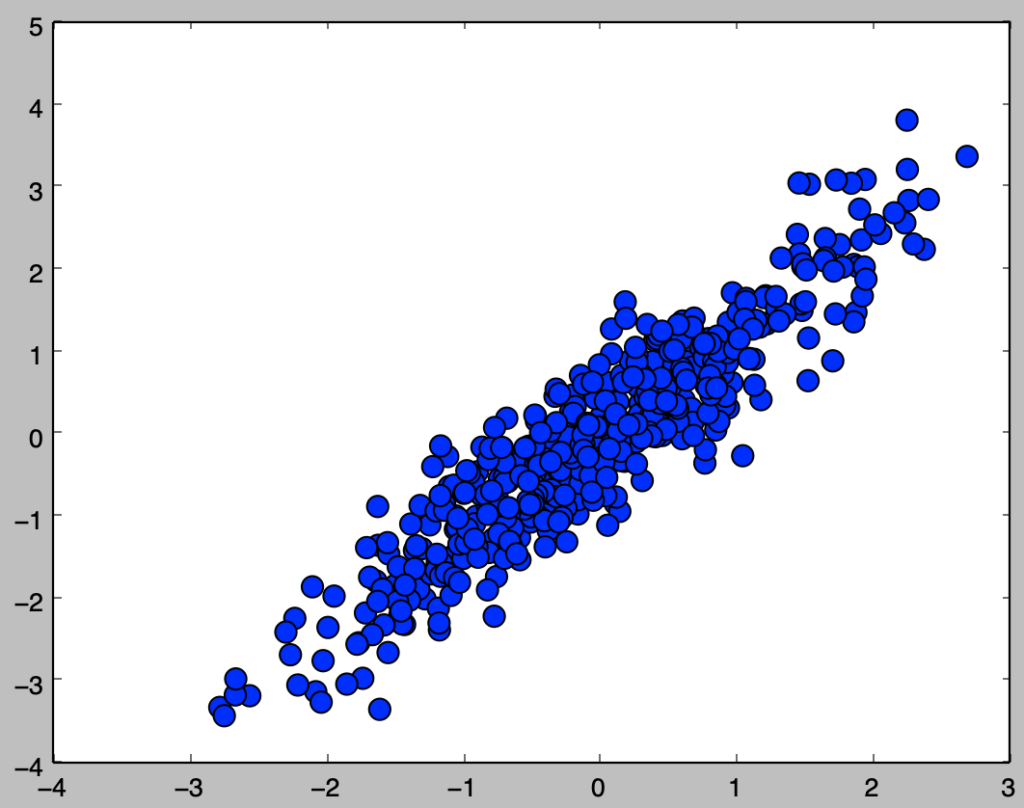
①Q.$1$-$1$-$4$のマーカーの大きさを変えよ。②●ではなく×に変え、同様に散布図の描画を行え。
・Q.$1$-$1$-$4$で生成を行うサンプル
np.random.seed(0)
x = stats.norm.rvs(size=500)
y = 1.2*x + 0.5*stats.norm.rvs(size=500)・解答①
plt.scatter(x,y,s=100)
plt.show()・実行結果①
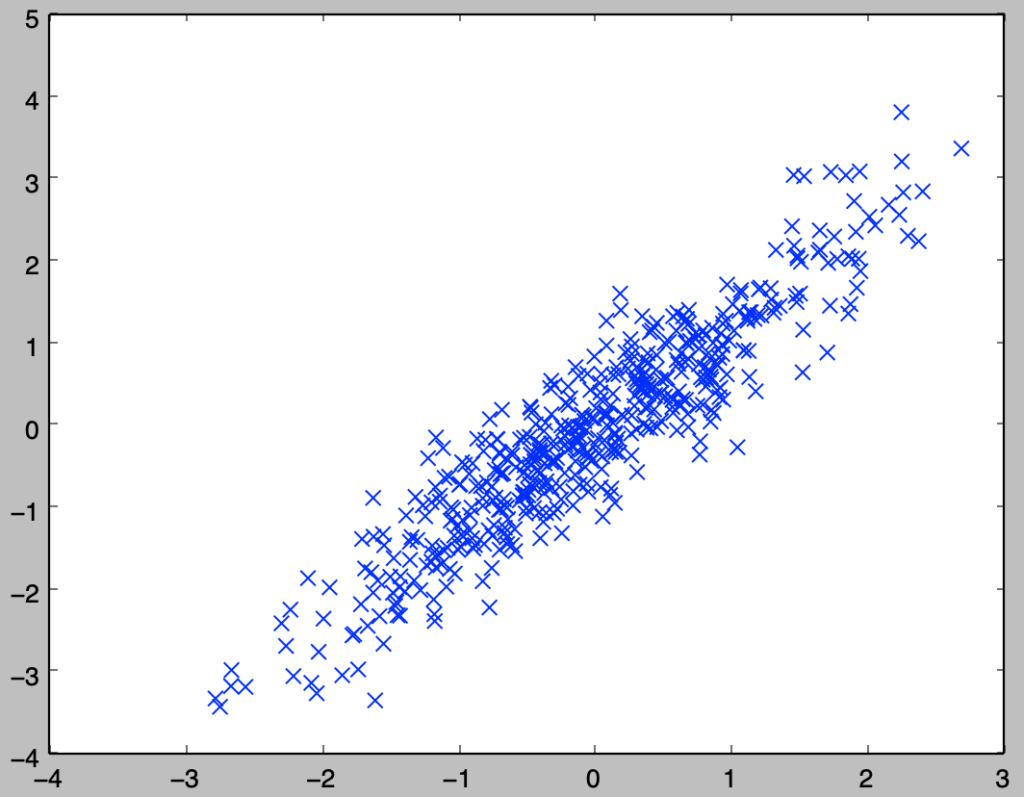
・解答②
plt.scatter(x,y,marker="x",s=50)
plt.show()・実行結果②
Q.1-2-9 図の描画順
x = np.array([1,2,3,4,5])
y = np.array([3.2, 2.1, 5.1, 1.2, 3.7])上記のQ.$1$-$1$-$2$の例に対し、折れ線グラフの上に各点の描画を行え。
・解答
plt.plot(x,y,zorder=1)
plt.scatter(x,y,s=50,zorder=2)
plt.show()・実行結果
プラスアルファで抑えておくと良い使い方
Q.1-3-1 複数グラフの描画
np.random.seed(0)
x = np.arange(-5.,5.1,0.1)
y = stats.norm.pdf(x)
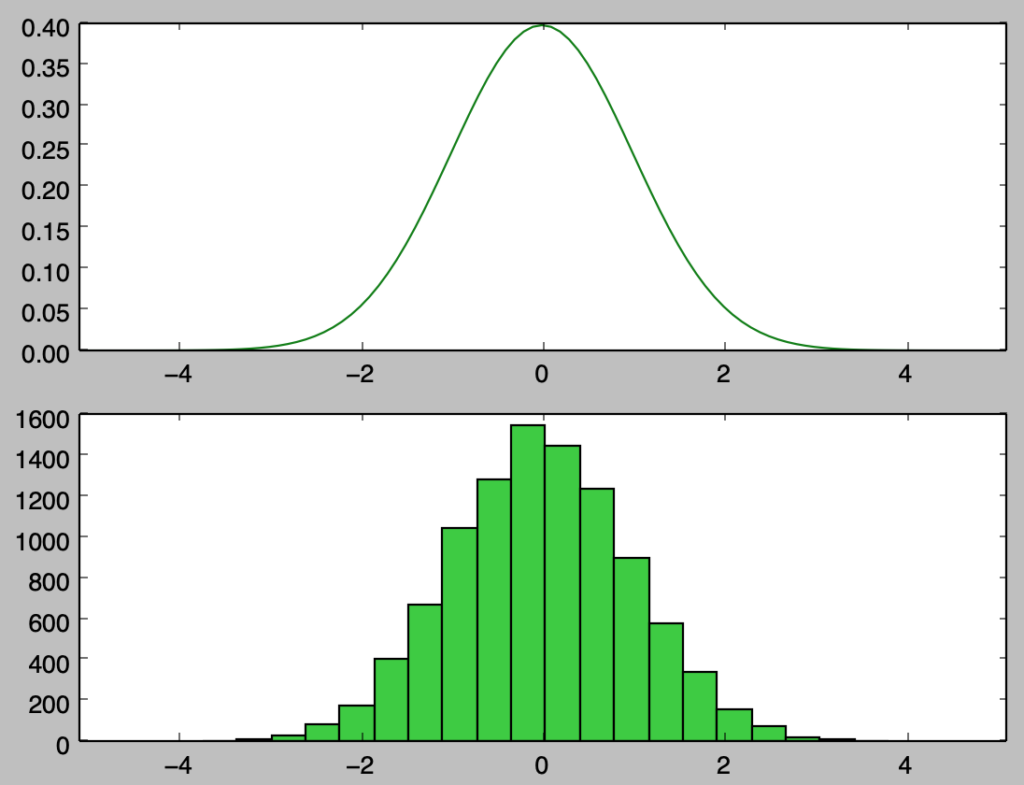
sampled_x = stats.norm.rvs(size=10000)標準正規分布$\mathcal{N}(0,1)$の確率密度関数である上記のyのグラフと、$\mathcal{N}(0,1)$からのサンプルであるsampled_xのグラフをそれぞれ上下配置で作成せよ。また、グラフの定義域は一致させよ。
・解答
plt.subplot(211)
plt.plot(x,y,color="green")
plt.xlim([-5.1,5.1])
plt.subplot(212)
plt.hist(sampled_x,bins=20,color="limegreen")
plt.xlim([-5.1,5.1])
plt.show()・実行結果
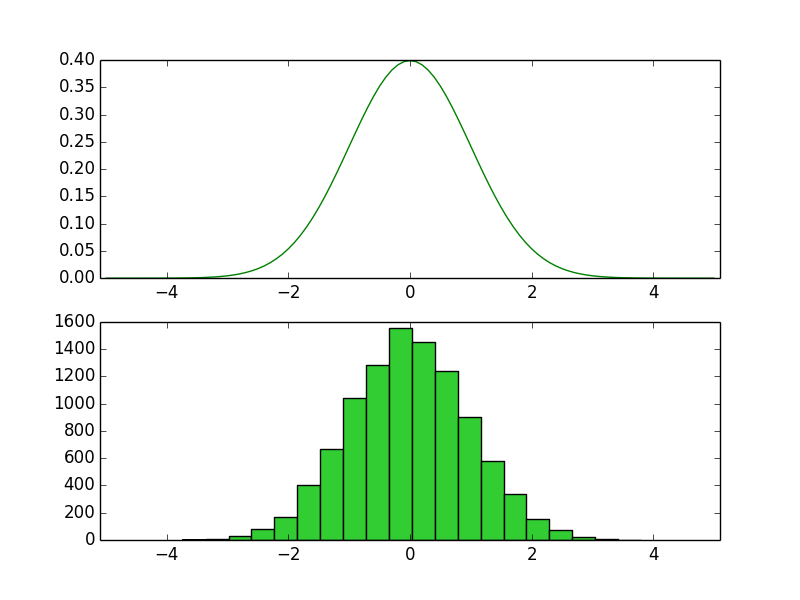
Q.1-3-2 グラフの保存
「Q.$1$-$3$-$1$ 複数グラフの描画」の結果をnorm1.pngに書き出せ。
・解答
plt.subplot(211)
plt.plot(x,y,color="green")
plt.xlim([-5.1,5.1])
plt.subplot(212)
plt.hist(sampled_x,bins=20,color="limegreen")
plt.xlim([-5.1,5.1])
plt.savefig("norm1.png")・実行結果 norm1.png

[…] 統計学を学ぶにあたって知っておくと良いMatplotlibの用法 […]