ローゼンブロック関数(Rosenbrock function)は主に$2$変数で表される関数で、シンプルな数式である一方で等高線が複雑になることから最適化アルゴリズムのベンチマークなどに用いられます。当記事ではローゼンブロック関数の数式とPythonを用いたグラフ化を取り扱いました。
・Pythonまとめ
https://www.hello-statisticians.com/python_basic
Contents
ローゼンブロック関数の数式と解釈
ローゼンブロック関数の数式
$2$変数$x,y$に関するローゼンブロック関数を$f(x,y)$とおくと、$f(x,y)$は下記のように表すことができます。
$$
\large
\begin{align}
f(x,y) = a(x-1)^{2} + b(y-x^2)^2
\end{align}
$$
上記の$a$と$b$はローゼンブロック関数のパラメータですが、一般的には$a=1, b=100$が用いられることが多いので、下記の式では数値の代入を行いました。
$$
\large
\begin{align}
f(x,y) = (x-1)^{2} + 100(y-x^2)^2
\end{align}
$$
ローゼンブロック関数の解釈
ローゼンブロック関数のグラフについては次節で取り扱いますが、Pythonなどを用いなくても数式から概形を予測することが可能です。式の解釈にあたっては$(y-x^2)^2$の係数が$100$のように大きい場合は$(y-x^2)^2$の項に着目すると良いです。
ここで$(y-x^2)^2$の項は、$y=x^2$が成立する際に$(y-x^2)^2=0$が成立するので、$y=x^2$の関数に沿ってローゼンブロック関数$f(x,y)$の値が小さいだろうと考察できます。
また、$y=x^2$が成立するとき$(x-1)^{2}$を最小にする$x$は$x=1$であるので、$(x,y)=(1,1)$が$f(x,y)$を最小にする点であると考えられます。このとき最小値は$f(1,1)=0$を取ります。ローゼンブロック関数では関数の値の小さな点が$y=x^2$の$0 \leq x \leq 2$あたりに集中することから等高線がバナナのような形を取ります。このことからローゼンブロック関数はバナナ関数などと呼ばれる場合もあります。
ローゼンブロック関数のグラフ化と最小点の探索
ローゼンブロック関数のグラフ化
下記を実行することで等高線を描くことができます。
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import LogNorm
x_, y_ = np.arange(-2,2.01,0.01), np.arange(-2,2.01,0.01)
x, y = np.meshgrid(x_, y_)
z = (1-x)**2 + 100*(y-x**2)**2
levs = 10**np.arange(0., 3.5, 0.5)
plt.contour(x,y,z,norm=LogNorm(),levels=levs,cmap="viridis")
plt.colorbar()
plt.show()・実行結果
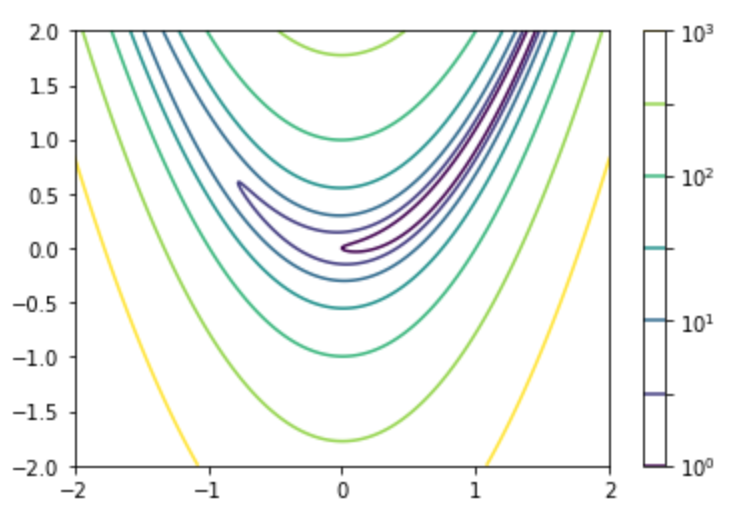
上図では黄色に近づくとローゼンブロック関数$f(x,y)$の値が大きく、紫に近づくと$f(x,y)$の値が小さいです。前節で解釈したように$y=x^2, \, 0 \leq x \leq 2$の周辺に関数の値が小さい点があることが確認できます。
勾配法を用いた関数の最小点の探索
$$
\large
\begin{align}
\left(\begin{array}{c} x_{n+1} \\ y_{n+1} \end{array} \right) = \left(\begin{array}{c} x_{n} \\ y_{n} \end{array} \right) – \alpha \nabla f(x,y)|_{x=x_{n},y=y_{n}}
\end{align}
$$
勾配降下法では上記のような数式を用いて関数の最小値の探索を行います。ここでローゼンブロック関数$f(x,y)$の勾配ベクトル$\nabla f(x,y)$は下記のように得られます。
$$
\large
\begin{align}
\nabla f(x,y) &= \left(\begin{array}{c} \displaystyle \frac{\partial f}{\partial x} \\ \displaystyle \frac{\partial f}{\partial y} \end{array} \right) \\
&= \left(\begin{array}{c} 2(x-1)-400x(y-x^2) \\ 200(y-x^2) \end{array} \right)
\end{align}
$$
上記の勾配ベクトルを元に下記を実行することで$(x,y)=(0,2)$から$\alpha=0.005$で勾配降下法の繰り返し計算を行うことができます。
alpha = 0.005
x_n, y_n = 0., 2.
for i in range(500):
x_n = x_n - alpha*(2*(x_n-1) - 400*x_n*(y_n-x_n**2))
y_n = y_n - alpha*200*(y_n-x_n**2)
if (i+1)%100==0:
print("n:{}, x_n:{:.5f}, y_n:{:.5f}".format(i+1,x_n,y_n))・実行結果
n:100, x_n:0.63397, y_n:0.40191
n:200, x_n:0.86602, y_n:0.74999
n:300, x_n:0.95096, y_n:0.90432
n:400, x_n:0.98205, y_n:0.96442
n:500, x_n:0.99343, y_n:0.98690上記よりx_nとy_nが$(1,1)$に収束することが確認できます。計算過程は次のように図で表すことも可能です。
alpha = 0.002
x_n, y_n = 0., 2.
x_n_, y_n_ = np.zeros(10), np.zeros(10)
display_n, display_idx = [1, 2, 5, 10, 20, 50, 100, 200, 500, 1000], 0
for i in range(1000):
x_n = x_n - alpha*(2*(x_n-1) - 400*x_n*(y_n-x_n**2))
y_n = y_n - alpha*200*(y_n-x_n**2)
if (i+1) in display_n:
x_n_[display_idx], y_n_[display_idx] = x_n, y_n
display_idx += 1
plt.plot(x_n_,y_n_,"ro")
plt.contour(x,y,z,norm=LogNorm(),levels=levs,cmap="viridis")
plt.colorbar()
plt.show()・実行結果
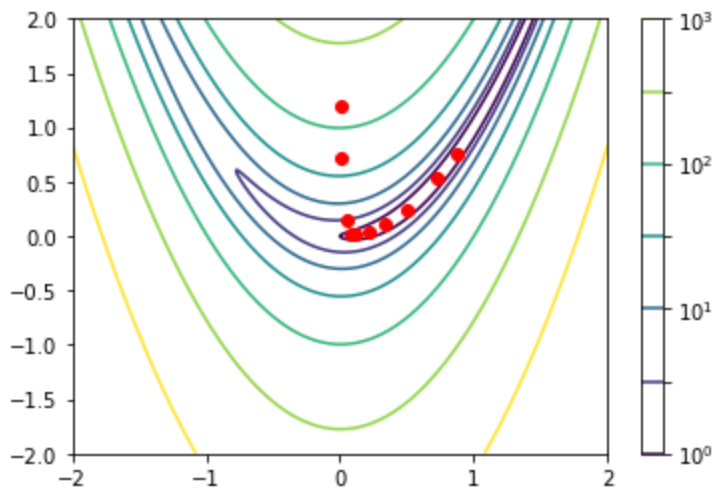
可視化の都合上学習率や表示する繰り返し演算のインデックスは調整を行いましたのでご注意ください。図より$(0,2)$から$(1,1)$に近づく流れが確認できます。
当項での計算では$\alpha$に定数を設定しましたが、下記のように直線探索を行うこともできます。
