双曲線関数(hyperbolic function)の定義と媒介変数表示を用いた双曲線の表現

双曲線関数(hyperbolic function)の$\sinh, \cosh, \tanh$はそれぞれ指数関数の$e^{x}$や$e^{-x}$を用いて定義されます。双曲線関数は双曲線を媒介変数表示する際に有用であるので、定義と使用例を合わせて抑えておくと良いと思います。
作成にあたっては「チャート式シリーズ 大学教養 微分積分」の第$2$章「関数($1$変数)」を主に参考にしました。

・数学まとめ
https://www.hello-statisticians.com/math_basic

チャート式シリーズ 大学教養 微分積分 (チャート式・シリーズ)

3,080円(04/27 12:26時点)

Amazon

双曲線関数の概要

双曲線関数の定義

双曲線関数の$\sinh{x}, \cosh{x}, \tanh{x}$はそれぞれ下記のように定義される。
$$
\large
\begin{align}
\sinh{x} &= \frac{e^{x}-e^{-x}}{2} \\
\cosh{x} &= \frac{e^{x}+e^{-x}}{2} \\
\tanh{x} &= \frac{\sinh{x}}{\cosh{x}} = \frac{e^{x}-e^{-x}}{e^{x}+e^{-x}}
\end{align}
$$

上記の$e^{x}, e^{-x}$が連続関数であるから、$\sinh{x}, \cosh{x}$は連続関数である。また、任意の$x$に関して$e^{x}+e^{-x}>0$であることから$\tanh{x}$も連続関数である。詳しくは「チャート式シリーズ 大学教養 微分積分」の基本例題$042$で確認すると良い。

双曲線関数のグラフ

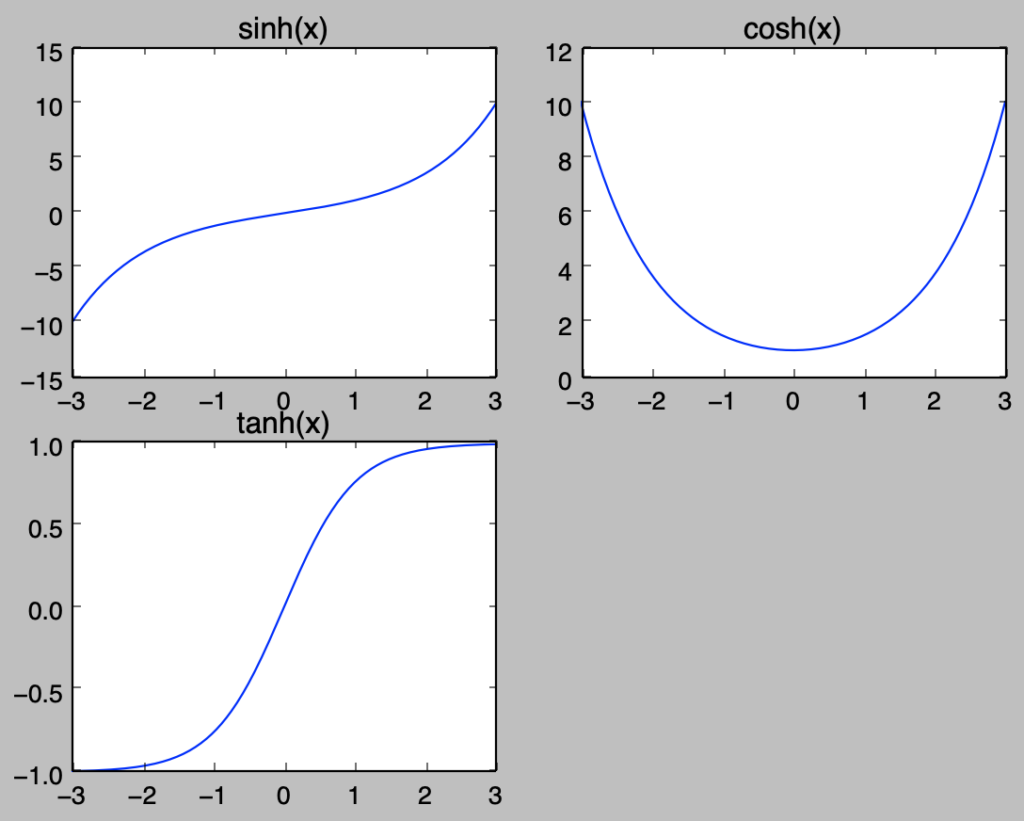
双曲線関数$\sinh{x}, \cosh{x}, \tanh{x}$のグラフはそれぞれ下記を実行することで作成できる。

import numpy as np
import matplotlib.pyplot as plt

x = np.arange(-3.,3.01,0.01)

y_sinh = (np.e**x-np.e**(-x))/2.
y_cosh = (np.e**x+np.e**(-x))/2.
y_tanh = (np.e**x-np.e**(-x))/(np.e**x+np.e**(-x))

plt.subplot(221)
plt.plot(x,y_sinh)
plt.title("sinh(x)")

plt.subplot(222)
plt.plot(x,y_cosh)
plt.title("cosh(x)")

plt.subplot(223)
plt.plot(x,y_tanh)
plt.title("tanh(x)")

plt.show()

・実行結果

双曲線関数の使用例

チャート式シリーズ 大学教養 微分積分 基本例題$043$

・$(1)$
$$
\large
\begin{align}
1 – \tanh^{2}{x} = \frac{1}{\cosh^{2}{x}}
\end{align}
$$

上記を示すにあたって、左辺の$1 – \tanh^{2}{x}$の変形を行う。
$$
\large
\begin{align}
1 – \tanh^{2}{x} &= 1 – \left( \frac{e^{x}-e^{-x}}{e^{x}+e^{-x}} \right)^{2} \\
&= \frac{(e^{x}+e^{-x})^2 – (e^{x}-e^{-x})^2}{(e^{x}+e^{-x})^2} \\
&= \frac{(e^{x}+e^{-x}+(e^{x}-e^{-x}))(e^{x}+e^{-x}-(e^{x}-e^{-x}))}{(e^{x}+e^{-x})^2} \\
&= \frac{2e^{x} \times 2e^{-x}}{(e^{x}+e^{-x})^2} \\
&= \frac{2^2}{(e^{x}+e^{-x})^2} \\
&= \frac{1}{\displaystyle \left( \frac{e^{x}+e^{-x}}{2} \right)^2} = \frac{1}{\cosh^{2}{x}}
\end{align}
$$

よって$\displaystyle 1 – \tanh^{2}{x} = \frac{1}{\cosh^{2}{x}}$が成立する。

・$(2)$
$$
\large
\begin{align}
\sinh{(x \pm y)} = \sinh{x}\cosh{y} \pm \cosh{x}\sinh{y}
\end{align}
$$

上記を示すにあたって、右辺の$\sinh{x}\cosh{y} \pm \cosh{x}\sinh{y}$の変形を行う。
$$
\large
\begin{align}
& \sinh{x}\cosh{y} \pm \cosh{x}\sinh{y} = \frac{e^{x}-e^{-x}}{2} \cdot \frac{e^{y}+e^{-y}}{2} \pm \frac{e^{x}+e^{-x}}{2} \cdot \frac{e^{y}-e^{-y}}{2} \\
&= \frac{(e^{x}-e^{-x})(e^{y}+e^{-y}) \pm (e^{x}+e^{-x})(e^{y}-e^{-y})}{2^2} \\
&= \frac{(e^{x+y}+e^{x-y}-e^{-x+y}-e^{-(x+y)}) \pm (e^{x+y}-e^{x-y}+e^{-x+y}-e^{-(x+y)})}{2^2} \\
&= \frac{2(e^{x \pm y}-e^{-(x \pm y)})}{2^2} \\
&= \frac{e^{x \pm y}-e^{-(x \pm y)}}{2} = \sinh{(x \pm y)}
\end{align}
$$

よって$\sinh{(x \pm y)} = \sinh{x}\cosh{y} \pm \cosh{x}\sinh{y}$が成立する。

・$(3)$
$$
\large
\begin{align}
\cosh{(x \pm y)} = \cosh{x}\cosh{y} \pm \sinh{x}\sinh{y}
\end{align}
$$

双曲線関数を用いた双曲線の媒介変数表示

$$
\large
\begin{align}
x(t) &= a \cosh{t} \\
y(t) &= a \sinh{t} \\
a &> 0
\end{align}
$$

上記のように媒介変数$t$を用いて$x(t),y(t)$を定める。このとき$x(t)^2-y(t)^2$は下記のように計算できる。
$$
\large
\begin{align}
x(t)^2 – y(t)^2 &= a^2 \cosh^{2}{t} – a^2 \sinh^{2}{t} \\
&= \frac{a^2}{2^2} [ (e^{x}+e^{-x})^2 – (e^{x}-e^{-x})^2 ] \\
&= \frac{a^2}{2^2} (e^{x}+e^{-x}+(e^{x}-e^{-x}))(e^{x}+e^{-x}-(e^{x}-e^{-x})) \\
&= \frac{a^2}{2^2} \cdot 2e^{x} \cdot 2e^{-x} \\
&= a^2
\end{align}
$$

よって$x(t) = a \cosh{t}, y(t) = a \sinh{t}$のように定めると$x(t)^2 – y(t)^2 = a^2$が成立する。ここで$x^2 – y^2 = a^2$は双曲線の方程式に一致するので$x(t) = a \cosh{t}, y(t) = a \sinh{t}$は双曲線の媒介変数表示であることが確認できる。

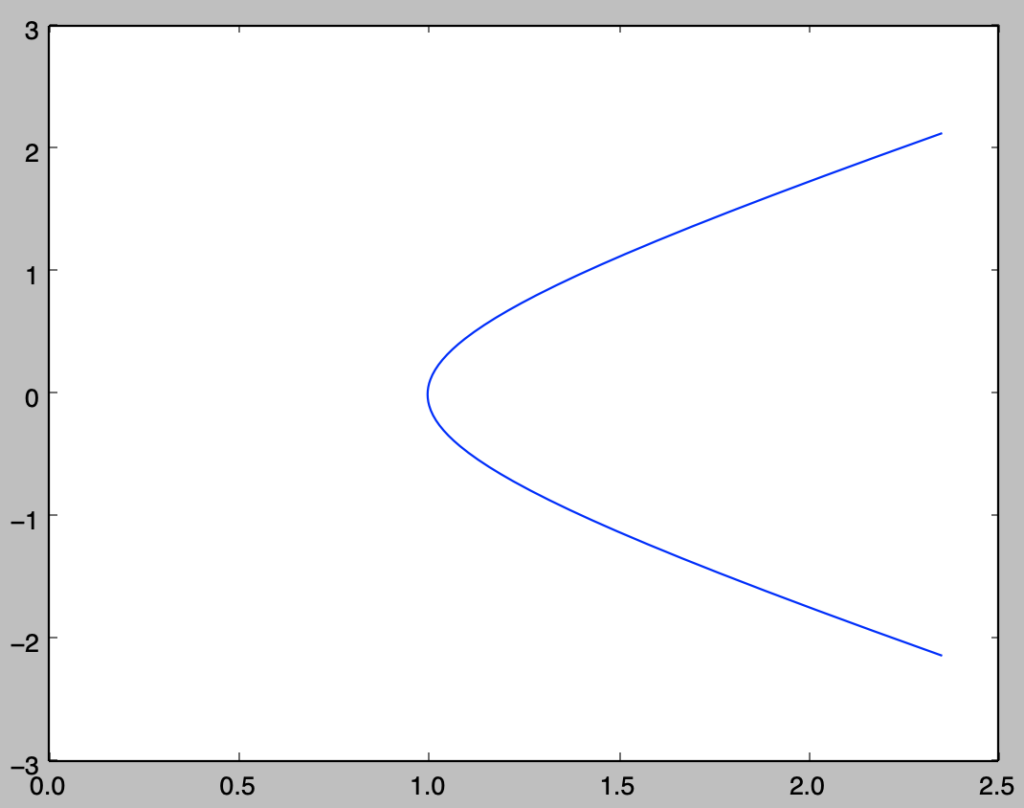
以下、双曲線関数の媒介変数表示を元に双曲線のグラフの描画を行う。下記を実行することで双曲線のグラフを描くことができる。

import numpy as np
import matplotlib.pyplot as plt

a = 1.
t = np.arange(-1.5,1.51,0.01)

x = a * (np.e**t + np.e**(-t))/2.
y = a * (np.e**t - np.e**(-t))/2. 

plt.plot(x,y)
plt.xlim([0.,2.5])
plt.show()

・実行結果