三角関数$\sin, \cos, \tan$の逆関数の$\sin^{-1}, \cos^{-1}, \tan^{-1}$は積分の結果の表記などでよく用いられるので、結果の解釈がしやすいように値に関して具体的に抑えておくと良いです。当記事では逆三角関数の値や方程式の解の計算に関して取りまとめました。
作成にあたっては「チャート式シリーズ 大学教養 微分積分」の第$2$章「関数($1$変数)」を主に参考にしました。
・数学まとめ
https://www.hello-statisticians.com/math_basic
逆三角関数の概要とグラフ
逆三角関数の概要
逆正弦関数$\sin^{-1}{x}$: 閉区間$\displaystyle \left[ -\frac{\pi}{2},\frac{\pi}{2} \right]$における正弦関数$\sin{x}$の逆関数
逆余弦関数$\cos^{-1}{x}$: 閉区間$[0,\pi]$における余弦関数$\cos{x}$の逆関数
逆正接関数$\tan^{-1}{x}$: 閉区間$\displaystyle \left[ -\frac{\pi}{2},\frac{\pi}{2} \right]$における正接関数$\tan{x}$の逆関数
上記の区間を定めなければ$x$に対応するそれぞれの関数の値が一意に定まらないので、区間を定める必要がある。この直感的理解に関しては次項でグラフを元に確認を行う。
逆三角関数のグラフ
「チャート式シリーズ 大学教養 微分積分」の基本例題$038$の内容を参考に、以下では逆三角関数のグラフに関して確認を行う。まず、三角関数$\sin, \cos, \tan$に関して、閉区間$\displaystyle \left[ -\frac{\pi}{2},\frac{\pi}{2} \right], [0,\pi], \left[ -\frac{\pi}{2},\frac{\pi}{2} \right]$におけるグラフは下記を実行することで描くことができる。
import numpy as np
import matplotlib.pyplot as plt
x1 = np.linspace(-np.pi/2.,np.pi/2.,100)
x2 = np.linspace(0.,np.pi,100)
y_sin = np.sin(x1)
y_cos = np.cos(x2)
y_tan = np.tan(x1)
plt.subplot(221)
plt.plot(x1,y_sin)
plt.title("sin(x)")
plt.xticks([-np.pi/2.,0,np.pi/2.],[r"$-\pi/2$",0,r"$\pi/2$"])
plt.subplot(222)
plt.plot(x2,y_cos)
plt.title("cos(x)")
plt.xticks([0,np.pi/2.,np.pi],[0,r"$\pi/2$",r"$\pi$"])
plt.subplot(223)
plt.plot(x1,y_tan)
plt.ylim([-3.,3.])
plt.title("tan(x)")
plt.xticks([-np.pi/2.,0,np.pi/2.],[r"$-\pi/2$",0,r"$\pi/2$"])
plt.show()・実行結果
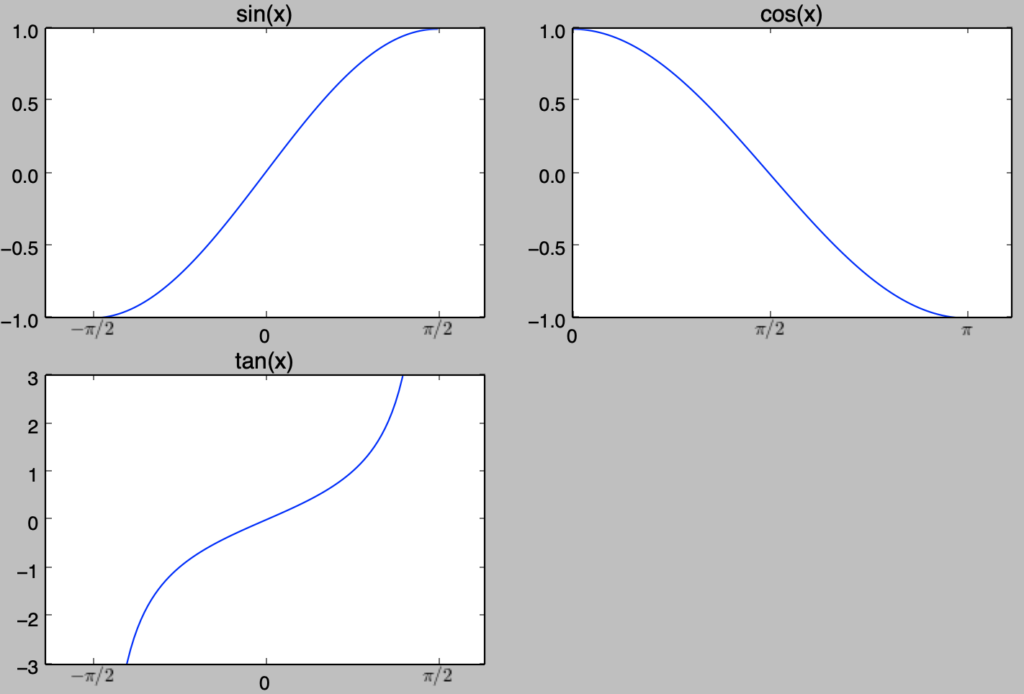
上記に対応する逆三角関数は下記のように図示を行うことができる。
import numpy as np
import matplotlib.pyplot as plt
x1 = np.linspace(-1., 1., 100)
x2 = np.linspace(-5., 5., 100)
y_arcsin = np.arcsin(x1)
y_arccos = np.arccos(x1)
y_arctan = np.arctan(x2)
plt.subplot(221)
plt.plot(x1,y_arcsin)
plt.title(r"$\sin^{-1}(x)$")
plt.yticks([-np.pi/2.,0,np.pi/2.],[r"$-\pi/2$",0,r"$\pi/2$"])
plt.subplot(222)
plt.plot(x2,y_arccos)
plt.title(r"$\cos^{-1}(x)$")
plt.yticks([0,np.pi/2.,np.pi],[0,r"$\pi/2$",r"$\pi$"])
plt.subplot(223)
plt.plot(x2,y_arctan)
plt.xlim([-3.,3.])
plt.title(r"$\tan^{-1}(x)$")
plt.yticks([-np.pi/2.,0,np.pi/2.],[r"$-\pi/2$",0,r"$\pi/2$"])
plt.show()・実行結果
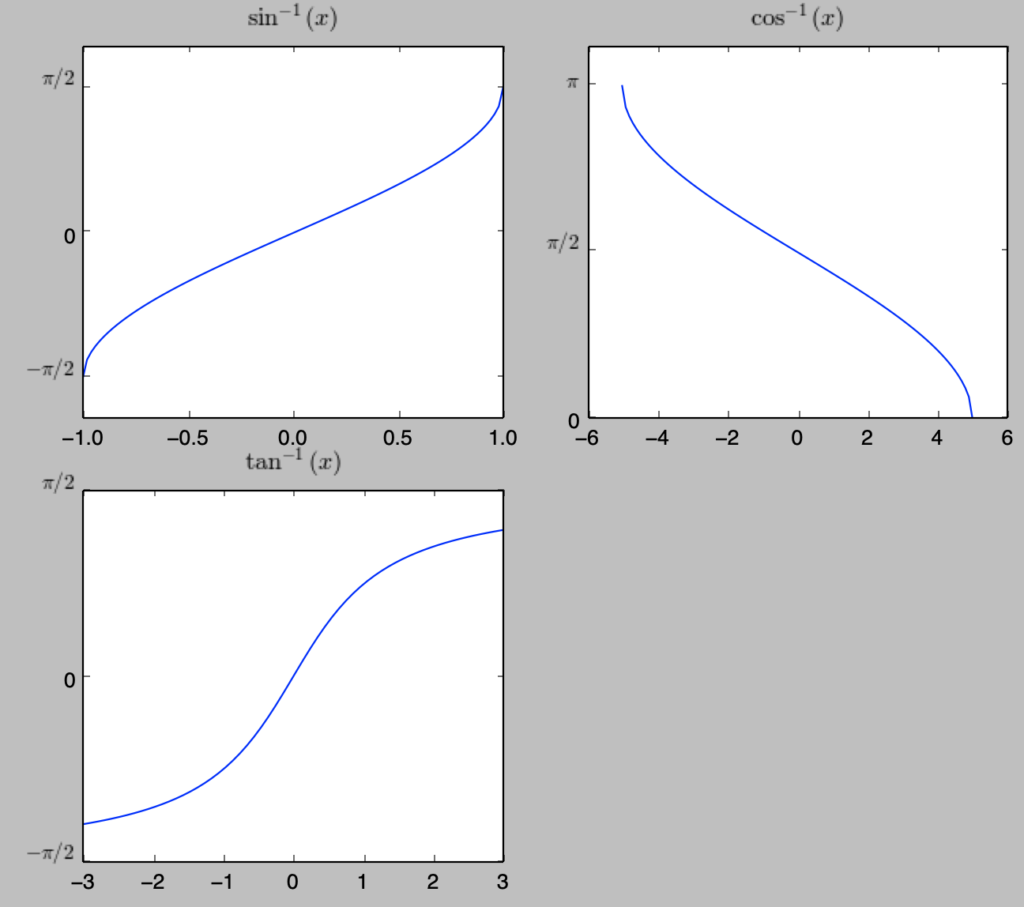
計算例
以下、「チャート式シリーズ 大学教養 微分積分」の例題の確認を行う。
基本例題$039$
・$(1)$
$$
\large
\begin{align}
\sin^{-1} \left( -\frac{1}{\sqrt{2}} \right), \quad -\frac{\pi}{2} \leq \sin^{-1} \left( -\frac{1}{\sqrt{2}} \right) \leq \frac{\pi}{2}
\end{align}
$$
上記の計算にあたって、$\displaystyle \sin^{-1} \left( -\frac{1}{\sqrt{2}} \right) = \alpha$とおき、$\alpha$に関して解く。
$$
\large
\begin{align}
\sin^{-1} \left( -\frac{1}{\sqrt{2}} \right) &= \alpha \\
\sin{\alpha} &= -\frac{1}{\sqrt{2}} \\
\alpha &= -\frac{\pi}{4}
\end{align}
$$
上記より、$\displaystyle \sin^{-1} \left( -\frac{1}{\sqrt{2}} \right) = -\frac{\pi}{4}$が得られる。
・$(2)$
$$
\large
\begin{align}
\cos^{-1} \left( -\frac{1}{2} \right), \quad 0 \leq \cos^{-1} \left( -\frac{1}{2} \right) \leq \pi
\end{align}
$$
上記の計算にあたって、$\displaystyle \cos^{-1} \left( -\frac{1}{2} \right) = \alpha$とおき、$\alpha$に関して解く。
$$
\large
\begin{align}
\cos^{-1} \left( -\frac{1}{2} \right) &= \alpha \\
\cos{\alpha} &= -\frac{1}{2} \\
\alpha &= \frac{2}{3} \pi
\end{align}
$$
上記より、$\displaystyle \sin^{-1} \left( -\frac{1}{\sqrt{2}} \right) = \frac{2}{3} \pi$が得られる。
・$(3)$
$$
\large
\begin{align}
\tan^{-1} \left( -\frac{1}{\sqrt{3}} \right), \quad -\frac{\pi}{2} \leq \tan^{-1} \left( -\frac{1}{\sqrt{3}} \right) \leq \frac{\pi}{2}
\end{align}
$$
上記の計算にあたって、$\displaystyle \tan^{-1} \left( -\frac{1}{\sqrt{3}} \right) = \alpha$とおき、$\alpha$に関して解く。
$$
\large
\begin{align}
\tan^{-1} \left( -\frac{1}{\sqrt{3}} \right) &= \alpha \\
\tan{\alpha} &= -\frac{1}{\sqrt{3}} \\
\alpha &= -\frac{\pi}{6}
\end{align}
$$
上記より、$\displaystyle \tan^{-1} \left( -\frac{1}{\sqrt{3}} \right) = -\frac{\pi}{6}$が得られる。
基本例題$040$
・$(1)$
・$(2)$
・$(3)$
