0-1損失関数のリスク関数(Risk Function)の導出と第1種・第2種の過誤の確率に関して

統計的決定理論の基本的な定義に関しては下記で取り扱った。
https://www.hello-statisticians.com/explain-terms-cat/stat_decision1.html
一方で、統計的決定理論は単体で取り扱うというよりも「推定論」や「検定論」と関連して抑える方が応用が見えてわかりやすい。
https://www.hello-statisticians.com/explain-terms-cat/roc1.html
上記では検定論の考え方に基づいてROC曲線やAUCの導出を行なったが、$0$-$1$損失関数のリスク関数の理解がやや難しいように思われた。

そこで当記事では$0$-$1$損失関数のリスク関数(Risk Function)の詳しい導出や、第1種の過誤・第2種の過誤の確率との関連について取りまとめを行なった。

リスク関数の定義

標本$x \in \mathscr{X}$、母数$\theta \in \Theta$、決定$d \in D$、決定関数$\delta: \mathscr{X} \to D$を考える。このとき、決定関数$\delta$の評価を行うにあたってはリスク関数$R(\theta,\delta)$を下記のように定義する。
$$
\large
\begin{align}
R(\theta,\delta) = E_{\theta}[L(\theta, d=\delta(x))]
\end{align}
$$

ここで損失関数は母数$\theta$と決定$d$に関して評価を行う一方で、リスク関数は母数$\theta$と決定関数$\delta$について評価を行うことに注意しておくと良い。

検定論における0-1損失関数

$0$-$1$損失関数は前項の決定空間$D$に対して$D = {0,1}$を取り扱う際に用いられる。この$0$-$1$損失関数を考える際は、母数空間$\Theta$を下記のように仮定する。
$$
\large
\begin{align}
\Theta &= \Theta_0 \cup \Theta_1 \\
\emptyset &= \Theta_0 \cap \Theta_1
\end{align}
$$

「母数空間$\Theta$は帰無仮説を表す空間$\Theta_0$と対立仮説を表す空間$\Theta_1$に排反でわけることができること」が上記の解釈である。背反は同時に起こらないことであり、積集合$\Theta_0 \cap \Theta_1$が空集合$\emptyset$であることから読み取ることができる。

ここで母数$\theta \in \Theta$と決定$d \in D={0,1}$に関して$0$-$1$損失関数を考えると、下記のように表すことができる。
$$
\large
\begin{align}
L(\theta,d=0) &= 0, \quad if \quad \theta \in \Theta_0 \\
&= 1, \quad if \quad \theta \in \Theta_1
\end{align}
$$
$$
\large
\begin{align}
L(\theta,d=1) = 1 – L(\theta,d=0)
\end{align}
$$

上記は数式だけ見ると難しいので、簡単に解釈を行う。$L(\theta,d=0)$は帰無仮説$d=0$を採択する際に、「母数$\theta$に関して帰無仮説が正しく、$\theta \in \Theta_0$が成立する場合」に$L(\theta,d=0)=0$、「母数$\theta$に関して対立仮説が正しく、$\theta \in \Theta_1$が成立する場合」に$L(\theta,d=0)=1$を返す関数であると解釈すればよい。また、$L(\theta,d=1)$は帰無仮説$d=0$を棄却し、対立仮説$d=0$を採択する場合について考えるので、$\theta \in \Theta_1$であれば$0$、$\theta \in \Theta_0$であれば$1$を返し、このことから$L(\theta,d=1) = 1 – L(\theta,d=0)$のように表すことができる。

下記で表した「現代数理統計学」の表8.1に基づいて理解するとわかりやすい。

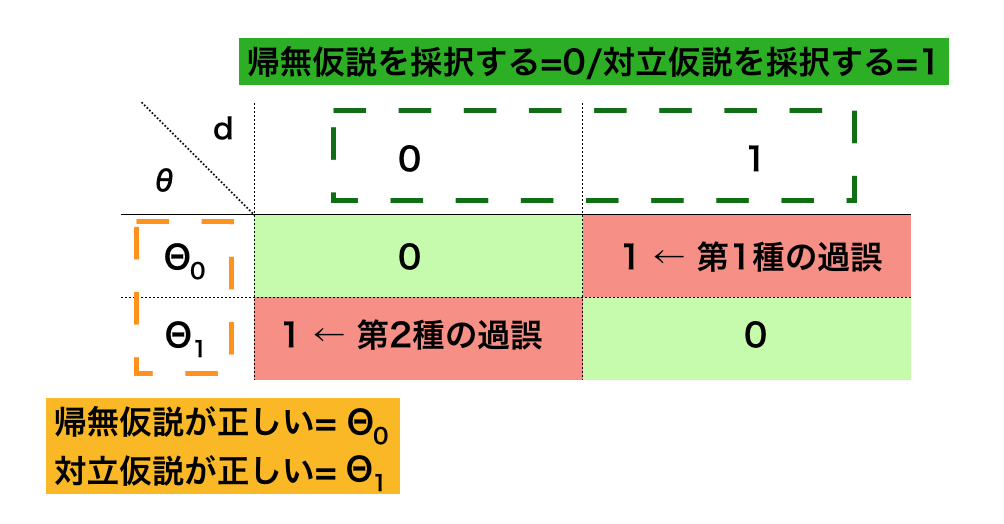
0-1損失関数のリスク関数

$$
\large
\begin{align}
L(\theta,d=0) &= 0, \quad if \quad \theta \in \Theta_0 \\
&= 1, \quad if \quad \theta \in \Theta_1
\end{align}
$$
$$
\large
\begin{align}
L(\theta,d=1) = 1 – L(\theta,d=0)
\end{align}
$$

$0$-$1$損失関数は上記のように表すことができた。損失関数は決定$d = 0$ or $1$に関して評価を行う関数であるので、決定関数$\delta$に関する評価も行えるとより良い。このときに用いられるのがリスク関数である。以下、$0$-$1$損失関数のリスク関数に関して考える。
$$
\large
\begin{align}
R(\theta,\delta) &= E_{\theta}[L(\theta, d=\delta(x))]
\end{align}
$$

リスク関数$R(\theta,\delta)$は上記のように定義されるが、ここで期待値を考えるにあたって$0$-$1$損失関数では$L = L(\theta, d=\delta(x)) = 0$ or $1$であることに着目することができる。

以下、$\theta \in \Theta_0$と$\theta \in \Theta_1$に分けてそれぞれリスク関数$R(\theta,\delta)$について考える。
・$\theta \in \Theta_0$の場合
$$
\large
\begin{align}
R(\theta,\delta) &= E_{\theta}[L(\theta, d={\delta}(x))] \\
&= 0 \times P(L(\theta, d=\delta(x))=0) + 1 \times P(L(\theta, d=\delta(x))=1) \\
&= P(L(\theta, d=\delta(x))=1)
\end{align}
$$
$\theta \in \Theta_0$より、上記の$(1)$式に対し$L(\theta, d=\delta(x))=1$が成立するのは$d=\delta(x)=1$のときである。よって、$R(\theta,{\delta})$は下記に一致する。
$$
\large
\begin{align}
R(\theta,{\delta}) &= P(L(\theta, d=\delta(x)=1)=1) \\
&= P(\delta(x)=1)
\end{align}
$$
母数に関して$\theta \in \Theta_0$が成立する際に決定に関して$d=1$が成立する確率は「第1種の過誤の確率」に一致する。

・$\theta \in \Theta_1$の場合
$(1)$式の導出までは$\theta \in \Theta_0$の場合と同様である。ここで$\theta \in \Theta_1$より、$(1)$式に対し$L(\theta, d=\delta(x))=1$が成立するのは$d=\delta(x)=0$のときである。よって、$R(\theta,{\delta})$は下記に一致する。
$$
\large
\begin{align}
R(\theta,{\delta}) &= P(L(\theta, d=\delta(x)=0)=1) \\
&= P(\delta(x)=0)
\end{align}
$$
母数に関して$\theta \in \Theta_1$が成立する際に決定に関して$d=0$が成立する確率は「第2種の過誤の確率」に一致する。