一様最強力検定を用いた二項分布に関する導出の流れの確認とネイマン・ピアソンの補題の解釈

当記事では一様最強力検定(Uniformly Most Powerful test)を考える際に用いられるネイマン・ピアソンの補題について取り扱った。そのままの形式では理解が難しいので、二項分布を用いた具体例を元に直感的な解釈を行なった。「現代数理統計学」の8章の「検定論」を参考に作成を行なった。

前提の確認

検出力(power)・検出力関数

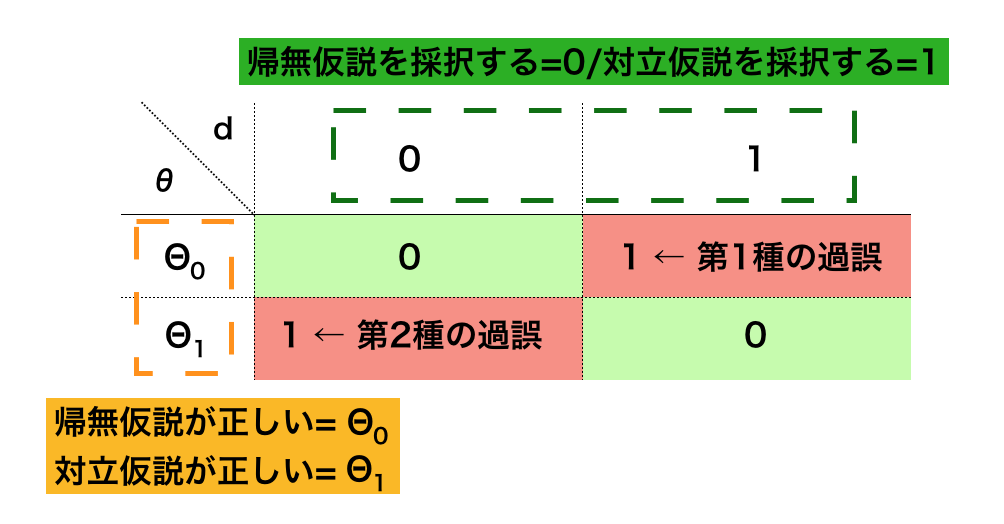
検定論では、決定$d \in D = \{0,1\}$と母数$\theta \in \Theta = \{\Theta_0,\Theta_1\}$、標本$x \in \mathscr{X}$、決定関数$\delta: \mathscr{X} \to D$に関して上記のように$0$-$1$損失関数$L(\theta, d=\delta(x))$を考えることで仮説検定を行う。

ここで、検定論に関して取り扱うにあたって、リスク関数を元に下記のように検出力関数(power function)$\beta_{\delta}(\theta)$が定義されるので抑えておく必要がある。
$$
\large
\begin{align}
\beta_{\delta}(\theta) = P(\delta(x)=1) = E[\delta(x)]
\end{align}
$$

検出力関数は「決定関数$\delta$によって帰無仮説を棄却する確率」であると考えることができる。よって、検出力関数を用いることでリスク関数$R(\theta,\delta)$は下記のように表すことができる。
$$
\large
\begin{align}
R(\theta,\delta) &= \beta_{\delta}(\theta) \qquad \theta \in \Theta_0 \\
&= 1-\beta_{\delta}(\theta) \quad \theta \in \Theta_1
\end{align}
$$

検出力関数は検定論の議論にあたってよく出てくるので抑えておくと良い。単に「決定関数$\delta$によって帰無仮説を棄却する確率」と理解しておけば十分であると思われる。

検定論と一様最強力検定

前項の内容について考える際に議論が必要なのが、「第1種の過誤と第2種の過誤の違いをどのように取り扱うべきか」である。これらに関しては様々な考え方があるが、検定論では「第1種の過誤を与えられた有意水準$\alpha$以下に抑えた上で対立仮説の検出力を最大にするのが良い」と伝統的に考える。

このような考え方に基づいて一様最強力検定(UMP; Uniformly Most Powerful test)が定義される。下記の検定問題に関して以下、一様最強力検定を考える。
$$
\large
\begin{align}
H_0 &: \quad \theta \in \Theta_0 \\
H_1 &: \quad \theta \in \Theta_1
\end{align}
$$

$\delta$を有意水準$\alpha$の任意の検定であると考えると、$\beta_{\delta}(\theta) \leq \alpha, \quad {}^{\forall} \theta \in \Theta_0$が成立する。このとき、下記が成立すれば検定$\delta^{*}$が一様最強力検定であるといえる。
$$
\large
\begin{align}
\beta_{\delta^{*}}(\theta) \geq \beta_{\delta}(\theta), \quad {}^{\forall} \theta \in \Theta_1
\end{align}
$$

一様最強力検定とネイマン・ピアソンの補題の解釈

単純仮説におけるネイマン・ピアソンの補題とその解釈

下記のように単純仮説を用いた検定を考える。
$$
\large
\begin{align}
H_0 &: \quad \theta = \theta_0 \\
H_1 &: \quad \theta = \theta_1
\end{align}
$$
上記を確認するにあたっては、帰無仮説と対立仮説を集合$\Theta_0,\Theta_1$ではなく、スカラー$\theta_0,\theta_1$を用いて表していることに注意すると良い。このように定義した単純仮説に対して、以下ネイマン・ピアソンの補題の確認を行う。

標本$x \in \mathscr{X}$に関して、$f(x,\theta_0)$を帰無仮説の「確率関数/確率密度関数」、$f(x,\theta_1)$を対立仮説の「確率関数/確率密度関数」と考える。以下、離散分布を元に考えるにあたり確率関数と表記するが、連続分布もほぼ同様の議論で考えることができる。

ここで$\delta_{c,r}(x)$を下記のように考える。
$$
\large
\begin{align}
\delta_{c,r}(x) &= 1, \quad if \quad \frac{f(x,\theta_1)}{f(x,\theta_0)} > c \\
&= r, \quad if \quad \frac{f(x,\theta_1)}{f(x,\theta_0)} = c \\
&= 0, \quad if \quad \frac{f(x,\theta_1)}{f(x,\theta_0)} < c
\end{align}
$$

このとき$0 \leq \alpha \leq 1$が成立する任意の有意水準$\alpha$に関して$\alpha = E[\delta_{c,r}(x)]$となる最強力検定$\delta_{c,r}(x)$が存在する。ここで「一様」がつかないのは対立仮説が単純対立仮説であるからである。

ここまでの解釈にあたっては、「$\delta_{c,r}(x)$が帰無仮説を棄却するかどうかを意味する」ことを改めて考えると良い。標本$x$に関して、対立仮説の確率関数$f(x,\theta_1)$が帰無仮説の確率関数$f(x,\theta_0)$の$c$倍より大きいとき、確率$1$で帰無仮説を棄却すると解釈できる。逆に標本$x$に関して、対立仮説の確率関数$f(x,\theta_1)$が帰無仮説の確率関数$f(x,\theta_0)$の$c$倍より小さいとき、確率$1$で帰無仮説を採択すると解釈することもできる。

また、$r$の解釈にあたっては、標本に関する確率変数$X$が離散であることから、有意水準を$\alpha$への調整が必要であると考えれば良い。

一様最強力検定

前項では帰無仮説と対立仮説に対し、集合ではなくスカラーを考える単純仮説を元に、ネイマン・ピアソンの補題により最強力検定に関して考えた。当項では前項のネイマン・ピアソンの補題に関する議論を単純仮説から複合仮説に基づく検定に拡張することで一様最強力検定について考える。

以下のような複合仮説に基づく検定を考える。
$$
\large
\begin{align}
H_0 &: \quad \theta \leq \theta_0 \\
H_1 &: \quad \theta > \theta_0
\end{align}
$$
$\theta$だとわかりにくい場合は、二項分布の確率$p$に関して下記のように考えることと同様に理解すれば良い。
$$
\large
\begin{align}
H_0 &: \quad p \leq p_0 \\
H_1 &: \quad p > p_0
\end{align}
$$

一般的な議論を行うにあたって、以下では$p$ではなく$\theta$を用いて、「現代数理統計学」の定理8.3の確認を行う。

・現代数理統計学の定理8.3より一部改変
$\theta$を$1$次元の母数と考え、確率関数が統計量$T(x)$に関して単調尤度比を持つと仮定し、下記の検定問題を考える。
$$
\large
\begin{align}
H_0 &: \quad \theta \leq \theta_0 \\
H_1 &: \quad \theta > \theta_0
\end{align}
$$
このとき任意の$0 \leq \alpha \leq 1$に対して$-\infty \leq c \leq \infty,0 \leq r \leq 1$が存在して、$\alpha$に関する下記の形式の一様最強力検定$\delta_{c,r}(x)$を考えることができる。
$$
\large
\begin{align}
\delta_{c,r}(x) &= 1, \quad if \quad T(x)>c \\
&= r, \quad if \quad T(x)=c \\
&= 0, \quad if \quad T(x)<c
\end{align}
$$

この定理をそのまま考えるとなかなか理解が難しいので、次項で二項分布の例に基づいて具体的に確認を行う。

二項分布の例に基づく一様最強力検定の解釈

前項で確認した「現代数理統計学」の定理8.3を二項分布に適用することを考える。

二項分布$Bin(n,p)$の事象が観測される回数を統計量$T(x)=x$とおく。このときパラメータ$p_1<p_2$となる$p_1,p_2$に関して下記のように尤度比を計算する。
$$
\large
\begin{align}
\frac{f(x,p_2)}{f(x,p_1)} &= \frac{{}_n C_x p_2^{x}(1-p_2)^{n-x}}{{}_n C_x p_1^{x}(1-p_1)^{n-x}} \\
&= \frac{p_2^{x}(1-p_2)^{n-x}}{p_1^{x}(1-p_1)^{n-x}} \\
&= \left( \frac{p_2(1-p_1)}{p_1(1-p_2)} \right)^{x} \times \left( \frac{1-p_1}{1-p_2} \right)^{n}
\end{align}
$$

上記において$p_{1}<p_{2}$なので$1-p_{1}>1-p_{2}$であり、$p_1(1-p_2)<p_2(1-p_1)$が成立する。よって、$\displaystyle \frac{p_2(1-p_1)}{p_1(1-p_2)} > 1$であり、尤度比は$T(x)=x$の単調増加関数となる。

ここまでの議論から、前項の定理より、下記のような一様最強力検定$\delta_{c,r}$を考えることができる。
$$
\large
\begin{align}
\delta_{c,r}(x) &= 1, \quad if \quad x>c \\
&= r, \quad if \quad x=c \\
&= 0, \quad if \quad x<c \quad (1)
\end{align}
$$
より詳しくは下記で表した「現代数理統計学」の章末課題8.3も参考になる。
https://www.hello-statisticians.com/explain-books-cat/math_stat_practice_ch8.html#83

以下では第1種の過誤の確率の$\alpha$から$c,r$を導出する。ネイマン・ピアソンの補題を実際に適用する際は$\alpha$から$c,r$を導出する形式で用いられることは抑えておく方が良い。
$$
\large
\begin{align}
H_0 &: \quad p \leq p_0 \\
H_1 &: \quad p > p_0
\end{align}
$$
上記のように帰無仮説$H_0$と対立仮説$H_1$を考える場合、$p_0$に関する確率関数を用いた一様最強力検定の期待値$E[\delta_{c,r}]$が$\alpha$に一致する。

「現代数理統計学」の二項分布の事例を用いて、$\displaystyle n=6,p_0=\frac{1}{2},\alpha=0.05$の具体的な値で確認を行う。このとき事象が起こる回数の確率変数を$X$と定義すると、$P(X=5),P(X=6)$は下記のように計算できる。
$$
\large
\begin{align}
P(X=5) &= {}_{6} C_5 \left( \frac{1}{2} \right)^{5} \left( 1 – \frac{1}{2} \right)^{1} \\
&= 6 \times \left( \frac{1}{2} \right)^{6} \\
&= 0.09375 \\
P(X=6) &= {}_{6} C_6 \left( \frac{1}{2} \right)^{6} \left( 1 – \frac{1}{2} \right)^{0} \\
&= 1 \times \left( \frac{1}{2} \right)^{6} \\
&= 0.015625
\end{align}
$$
上記より、$P(X=6)=0.015625<0.05=\alpha$かつ$P(X \geq 5)=P(X=5)+P(X=6)=0.109375>0.05=\alpha$より、$c=5$であることがわかる。

このとき$r$は下記のように計算することができる。
$$
\large
\begin{align}
r &= \frac{\alpha – P(X=6)}{P(X=5)} \\
&= \frac{0.05 – 0.015625}{0.09375} \\
&= 0.3666…
\end{align}
$$
よって、一様最強力検定は$\delta_{5,0.3667}$であると考えることができる。また、ここまでの議論より、$0.05=P(X=6)+0.3667P(X=5)$が成立することもわかる。

一様最強力検定はここまでの流れと同様に考えることができるので、下記のような手順で考えておけば良い。

1) 尤度比が統計量の単調増加関数であることを確認する。
2) ネイマン・ピアソンの補題により、統計量T(x)に対して閾値cの一様最強力検定が存在する。
3) 期待値が第1種の過誤の確率のαに一致することから、cとrを計算する。

また、$c$は統計量$T(x)$に関する閾値、$r$は離散分布における$\alpha$の値の調整だと解釈しておくとよい。