統計的決定理論・検定論に基づくROC曲線・AUC(Area Under the Curve)の導出

ROC曲線(Receiver Operating Characteristic curve)やそれに基づくAUC(Area Under the Curve)は様々な場面で用いられるが、これらは統計的決定理論や検定論に基づいて導出することができる。当記事では「現代数理統計学」の5章や8.3節の内容を参考に、取りまとめを行なった。

前提の確認

点推定・検定論における標本空間と決定空間

$$
\large
\begin{align}
\delta : \quad \mathscr{X} \to D
\end{align}
$$
標本空間$\mathscr{X}$から決定空間$D$への関数を$\delta$とおくと、上記のように$\delta$を定義できる。この$\delta$を決定関数(decision function)という。

点推定では、上記の標本空間$\mathscr{X}$が$X_1,X_2,…,X_n$のように表される観測値の確率変数、決定空間$D$が母平均$\mu$のような推定するパラメータに対応する。たとえば母平均の推定値の$\hat{\mu}$を計算するにあたって、下記のように標本平均に関する確率変数を計算することが$\delta$の例に考えられる。
$$
\large
\begin{align}
\hat{\mu} &= \delta(X_1,X_2,…,X_n) \\
&= \frac{1}{n} \sum_{i=1}^{n} X_i
\end{align}
$$

ここまでで統計的決定理論を用いた点推定について確認を行なったが、検定論では上記のように推定を行う母平均の推定量$\hat{\mu}$の推定値に対して、帰無仮説と対立仮説を設定し、検定を行うことを考える。

たとえば母平均$\mu$に関して下記のような帰無仮説$H_0$と対立仮説$H_1$を設定し、推定量$\hat{\mu}$を用いて仮説検定を行うことなどが考えられる。
$$
\large
\begin{align}
H_0: \quad \mu = \mu_0 \\
H_1: \quad \mu \neq \mu_0
\end{align}
$$

上記に対しては標準正規分布の上側2.5％点を$z_{\alpha=0.025}$とおき、$\hat{\mu}$に関して$\displaystyle \mu_0-\frac{\sigma}{\sqrt{n}}z_{\alpha=0.025} \leq \hat{\mu} \leq \mu_0+\frac{\sigma}{\sqrt{n}}z_{\alpha=0.025}$が成立するかどうかで検定を行うのが一つの方法である。

標本空間・決定空間・決定関数に関しては詳しくは下記で取り扱った。
https://www.hello-statisticians.com/explain-terms-cat/stat_decision1.html#i
https://www.hello-statisticians.com/explain-terms-cat/stat_decision1.html#i-3

点推定・検定論における損失関数

損失関数(loss function)は回帰などでよく出てくるが、推定結果の「妥当さ」を表す関数であり、二乗誤差や0-1損失が用いられることが多い。たとえばパラメータ推定の場合は母数$\theta$と母数の推定値$\hat{\theta}$に関して、下記のように損失関数$L(\theta,\hat{\theta})$を二乗誤差で表せる。
$$
\large
\begin{align}
L(\theta,\hat{\theta}) = (\theta – \hat{\theta})^2
\end{align}
$$

以下では検定論について考えるので、二乗誤差ではなく0-1損失を元に確認を行う。

$$
\large
\begin{align}
\delta : \quad \mathscr{X} \to D
\end{align}
$$
前節で上記のような決定関数$\delta$を確認したが、点推定ではパラメータ$\theta$の推定値$\hat{\theta}$を決定空間に考えた一方で、検定論では「受容$0$/棄却$1$」を決定空間に考える。また、母数$\theta$は帰無仮説を表す$\Theta_0$と対立仮説を表す$\Theta_1$の2つの集合で考えられる。

よって、検定論では$\Theta_0, \Theta_1$の2つの母数空間と受容$0$/棄却$1$の2値の決定が対応すると考えることができる。これに対して、$0-1$損失の$L(\theta,d)$を考えると、$L(\theta,d)$は下記のように表すことができる。
$$
\large
\begin{align}
L(\theta,d=0) &= 0, \quad if \quad \theta \in \Theta_0 \\
&= 1, \quad if \quad \theta \in \Theta_1 \\
L(\theta,d=1) &= 1, \quad if \quad \theta \in \Theta_0 \\
&= 0, \quad if \quad \theta \in \Theta_1 \\
L(\theta,d=1) &= 1 – L(\theta,d=0)
\end{align}
$$

損失関数とリスク関数

検定における決定$d \in \{0, 1\}$が観測値を表す確率変数の$X_1,X_2,…,X_n$によって変動する以上、損失関数が確率的に変動することは考慮せねばならない。この対応にあたって損失関数の期待値を考えるのがリスク関数である。リスク関数は下記のように損失関数の期待値を考える。
$$
\large
\begin{align}
\hat{\theta} &= \delta(X_1,X_2,…,X_n) \\
L(\theta,\hat{\theta}) &= (\theta-\hat{\theta})^2 \\
R(\theta,\delta) &= E[L(\theta,\hat{\theta}=\delta(X_1,X_2,…,X_n))]
\end{align}
$$

上記は$\theta$に関する点推定を行う際二乗誤差を元にリスク関数を定義した。以下では検定論に関連して$0-1$損失関数を確認する。
$$
\large
\begin{align}
d &= \delta(X_1,X_2,…,X_n) \\
L(\theta,d=0) &= 0, \quad if \quad \theta \in \Theta_0 \\
&= 1, \quad if \quad \theta \in \Theta_1 \\
L(\theta,d=1) &= 1 – L(\theta,d=0) \\
R(\theta,\delta) &= E[L(\theta,d=\delta(X_1,X_2,…,X_n))]
\end{align}
$$

ここでリスク関数$R(\theta,\delta)$は母数$\theta$と決定関数$\delta$に関する関数であることは抑えておくと良い。

標本空間$\mathscr{X} = \{0,1\}$の際のリスク点の描画

標本空間$\mathscr{X} = \{0,1\}$に対して決定空間$D = \{0,1\}$と母数空間$\Theta = \{\theta_0,\theta_1\}, \theta_0 < \theta_1$を考える。
$$
\large
\begin{align}
\delta : \quad \mathscr{X} \to D
\end{align}
$$
このとき上記のように決定関数$\delta$を用いて標本空間から決定空間への写像を考える。2値から2値への関数であるので、$\delta$には下記の4通りが考えられる。

A) Xの値に関わらずd=0
B) Xの値に関わらずd=1
C) X=1ならばd=1、X=0ならばd=0
D) X=1ならばd=0、X=0ならばd=1

ここでAを$\delta_1$、Bを$\delta_2$、Cを$\delta^{*}$、Dを$\delta_{*}$のように考える。このとき、下記で表したような「現代数理統計学」の$(5.10)$式が成立する。
$$
\large
\begin{align}
R(\theta,\delta_0) &= 0, \quad if \quad \theta = \theta_0 \\
&= 1, \quad if \quad \theta = \theta_1 \\
R(\theta,\delta_1) &= 1 – R(\theta,\delta_0)
\end{align}
$$
$$
\large
\begin{align}
R(\theta,\delta^{*}) &= \theta_0, \qquad if \quad \theta = \theta_0 \\
&= 1-\theta_1, \quad if \quad \theta \in \theta_1 \\
R(\theta,\delta_{*}) &= 1 – R(\theta,\delta^{*})
\end{align}
$$
上記の$\delta^{*}$を理解するにあたっては、損失関数が$1$となる場合、「母数が$\theta_0$の際は$d=1$、母数が$\theta_1$の際は$d=0$であること」を元に損失関数の期待値を計算すると考えると良い。詳しくは下記で取り扱った。
https://www.hello-statisticians.com/explain-terms-cat/stat_decision2.html

やや議論が抽象的なので、以下では$\displaystyle \theta_0=\frac{1}{2}, \theta_1=\frac{2}{3}$を元に具体的にリスク点$(R(\theta_0,\delta),R(\theta_1,\delta))$を計算し、描画を行う。
・Aのリスク点
$$
\large
\begin{align}
R(\theta_0,\delta_0) &= 0 \\
R(\theta_1,\delta_0) &= 1
\end{align}
$$
・Bのリスク点
$$
\large
\begin{align}
R(\theta_0,\delta_1) &= 1 \\
R(\theta_1,\delta_1) &= 0
\end{align}
$$
・Cのリスク点
$$
\large
\begin{align}
R(\theta_0,\delta^{*}) &= \theta_0 \\
&= \frac{1}{2} \\
R(\theta_1,\delta^{*}) &= 1-\theta_1 \\
&= 1-\frac{2}{3} \\
&= \frac{1}{3}
\end{align}
$$
・Dのリスク点
$$
\large
\begin{align}
R(\theta_0,\delta_{*}) &= 1-R(\theta_0,\delta^{*}) \\
&= 1-\frac{1}{2} \\
R(\theta_1,\delta_{*}) &= 1-R(\theta_1,\delta^{*}) \\
&= 1-\frac{2}{3} \\
&= \frac{1}{3}
\end{align}
$$

ここまでの議論より、A〜Dのリスク点は下記のように描画することができる。

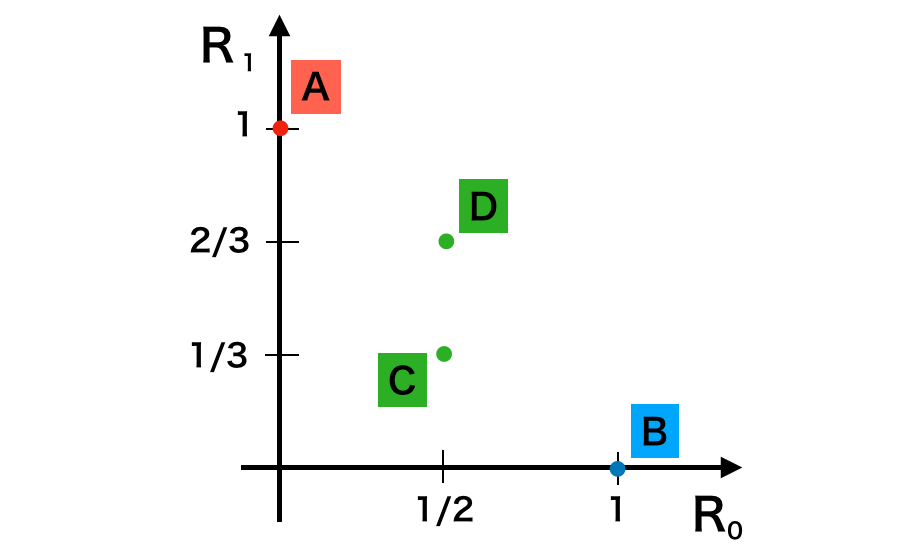
上図で描画を行なったリスク点を元に考える際は、基本的に左下が適切な決定方式で、右上が不適切な決定方式であることを理解しておくと良い。

確率化決定方式とリスク点

確率化決定方式(randomized decision process)を用いることで、下記の点線やその内部で囲まれた領域もリスク点に考えることができるようになる。

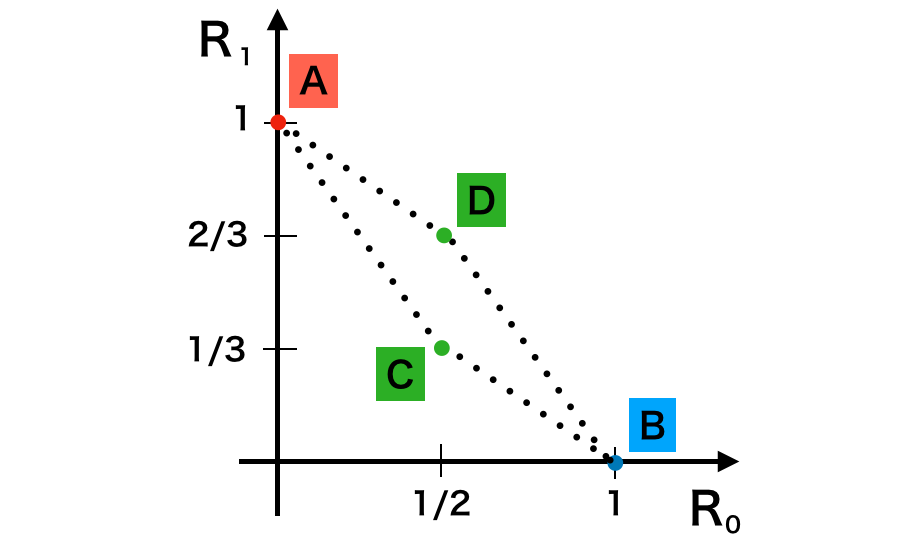
確率$\alpha$で$\delta_{0}$を適用し、確率$1-\alpha$で$\delta^{*}$を適用するような確率化決定方式を$\delta_{\alpha}$とするとき、上記の$A$と$C$を結ぶ線分が$\delta_{\alpha}$のリスク点$(R(\theta_0,\delta_{\alpha}),R(\theta_1,\delta_{\alpha}))$の軌跡に一致する。

また、$\delta_{\alpha}$のリスク関数は下記のように定義できる。
$$
\large
\begin{align}
R(\alpha,\delta_{\alpha}) = \alpha R(\theta,\delta_{0}) + (1-\alpha) R(\theta,\delta^{*}) \quad (1)
\end{align}
$$

上記に関しては詳しくは下記の議論より導出できる。
https://www.hello-statisticians.com/explain-books-cat/math_stat_practice_ch5.html#53

ROC曲線・AUCの導出

リスク関数と第1種の過誤・第2種の過誤

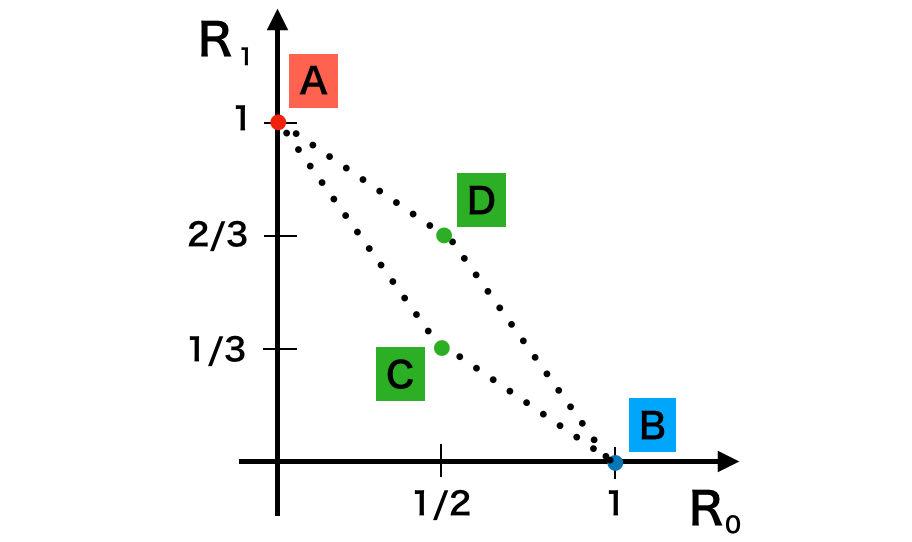
検定論では上図における$R_0$は第1種の過誤の確率$\alpha$、$R_1$は第2種の過誤の確率にそれぞれ対応すると考える。

また、一様最強力検定(UMP test; Uniformly Most Powerful test)は第1種の過誤の確率に関連して有意水準の$\alpha$を考え、$\alpha$を固定した際に第2種の過誤の確率を最も小さくする「仮説」を元に検定を行うことを意味する。このことより、図における線分$AC$と線分$CB$上の点がそれぞれ一様最強力検定を表すと考えれば良いことがわかる。

ROC曲線とAUC

リスク点での議論における縦軸の$R_1$を$1-R_1$で置き換えることによって反転させることで下図が得られる。

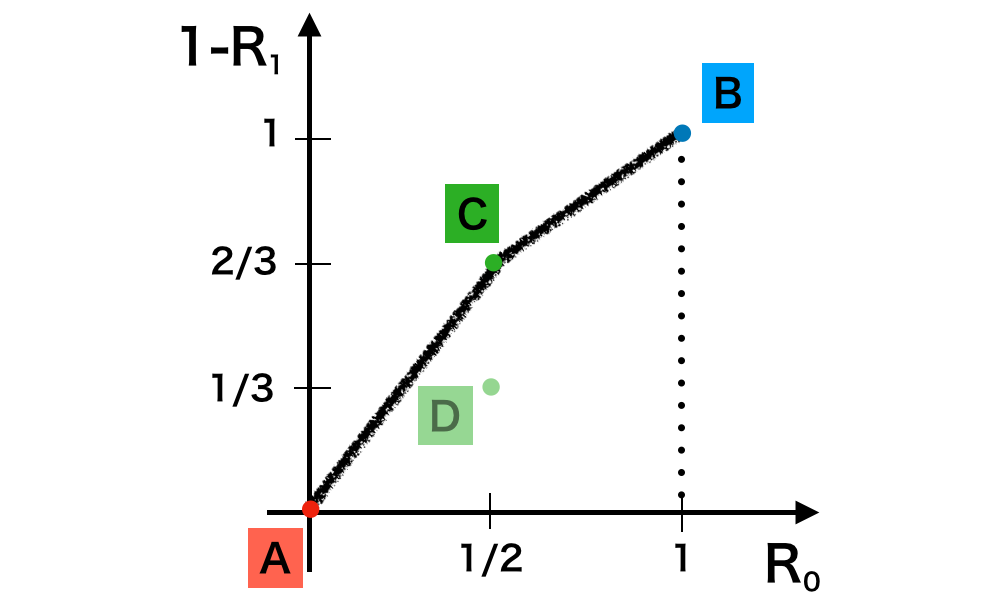
上記の$A,C$、$C,B$を結ぶ直線がROC曲線(Receiver Operating Characteristic curve)、線分$AC$、線分$CB$と$1-R_1=0, R_0=1$で囲まれる部分の面積をAUC(Area Under the Curve)に対応する。