三角関数の加法定理・倍角の公式・極限、微分の公式の簡易的な導出とその直感的理解

三角関数の「加法定理」・「倍角の公式」・「極限、微分の公式」は高校数学の主要なトピックであり、様々な専門領域の基礎になるが、公式を適用することが中心になりがちで、導出まで抑えているケースが少ないと思われる。
そこで当記事では「加法定理」・「倍角の公式」・「極限、微分の公式」に関して簡易的な導出を取りまとめることで、それぞれの直感的な理解が可能になるように取り扱った。

加法定理・倍角の公式

$\displaystyle \tan{\alpha} = \frac{\sin{\alpha}}{\cos{\alpha}}$とできることより、以下では$\sin, \cos$のみ計算し、$\tan$に関する導出は行わない。

加法定理

加法定理の導出にあたっては様々な方法があるが、三角関数が三角比に基づいて理解できることも考慮すると、図形的に示せる方が良いと思われる。よって、以下では図を用いたシンプルな導出を示す。

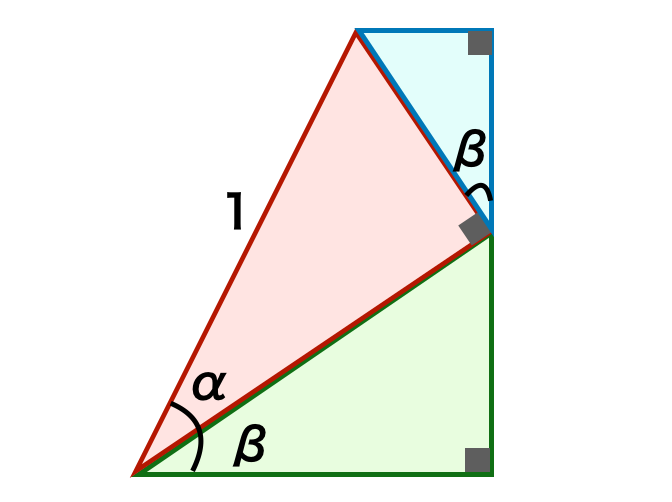
上図を用いることで、$\sin{(\alpha+\beta)}, \cos{(\alpha+\beta)}$の導出を行うことができ、$\sin{(\alpha+\beta)}, \cos{(\alpha+\beta)}$から$\sin{(\alpha-\beta)}, \cos{(\alpha-\beta)}$の導出を行うこともできる。

・$\sin{(\alpha+\beta)} = \sin{\alpha}\cos{\beta} + \cos{\alpha}\sin{\beta}$の導出

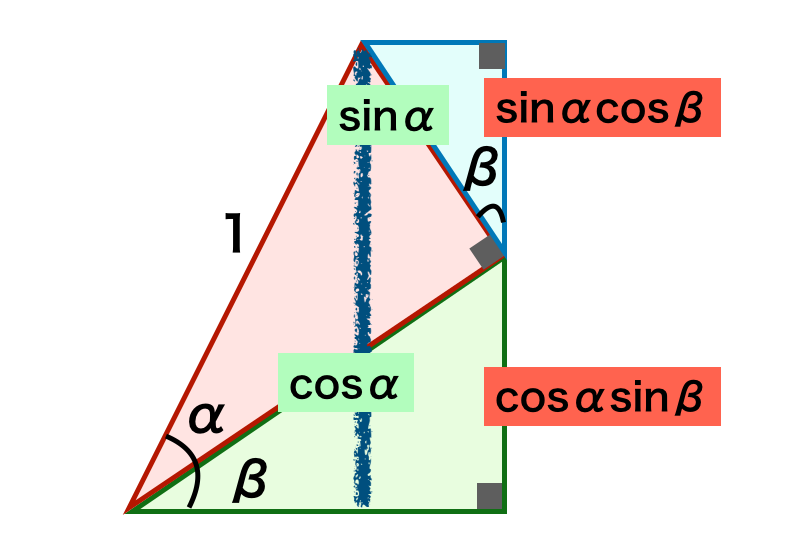
上図より$\sin{(\alpha+\beta)} = \sin{\alpha}\cos{\beta} + \cos{\alpha}\sin{\beta}$が導出できる。

・$\cos{(\alpha+\beta)} = \cos{\alpha}\cos{\beta} – \sin{\alpha}\sin{\beta}$の導出

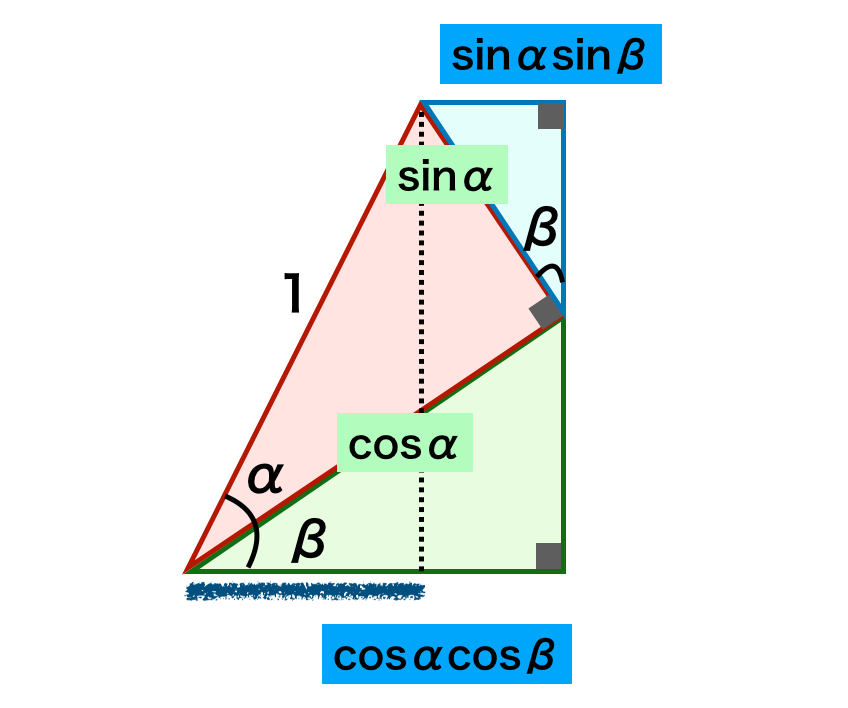
上図より$\cos{(\alpha+\beta)} = \cos{\alpha}\cos{\beta} – \sin{\alpha}\sin{\beta}$が導出できる。

・$\sin{(\alpha-\beta)}, \cos{(\alpha-\beta)}$の導出
$$
\large
\begin{align}
\sin{(\alpha+\beta)} &= \sin{\alpha}\cos{\beta} + \cos{\alpha}\sin{\beta} \\
\cos{(\alpha+\beta)} &= \cos{\alpha}\cos{\beta} – \sin{\alpha}\sin{\beta}
\end{align}
$$
上記の$\beta$に$-\beta$を代入することでそれぞれ導出を行うことができる。

ここまでの議論により、下記のような三角関数の加法定理の式が得られる。
$$
\large
\begin{align}
\sin{(\alpha+\beta)} &= \sin{\alpha}\cos{\beta} + \cos{\alpha}\sin{\beta} \\
\sin{(\alpha-\beta)} &= \sin{\alpha}\cos{\beta} – \cos{\alpha}\sin{\beta} \\
\cos{(\alpha+\beta)} &= \cos{\alpha}\cos{\beta} – \sin{\alpha}\sin{\beta} \\
\cos{(\alpha-\beta)} &= \cos{\alpha}\cos{\beta} + \sin{\alpha}\sin{\beta}
\end{align}
$$

倍角の公式

2倍角の公式

$$
\large
\begin{align}
\sin{(\alpha+\beta)} &= \sin{\alpha}\cos{\beta} + \cos{\alpha}\sin{\beta} \\
\cos{(\alpha+\beta)} &= \cos{\alpha}\cos{\beta} – \sin{\alpha}\sin{\beta}
\end{align}
$$
上記の加法定理の公式に対して$\beta=\alpha$を代入することで導出ができる。

$$
\large
\begin{align}
\sin{(2 \alpha)} &= \sin{(\alpha+\alpha)} \\
&= \sin{\alpha}\cos{\alpha} + \cos{\alpha}\sin{\alpha} \\
&= 2 \sin{\alpha}\cos{\alpha} \\
\cos{(2 \alpha)} &= \cos{(\alpha+\alpha)} \\
&= \cos{\alpha}\cos{\alpha} – \sin{\alpha}\sin{\alpha} \\
&= \cos^2{\alpha} – \sin^2{\alpha}
\end{align}
$$

3倍角の公式

$3\alpha=2\alpha+\alpha$と考えて加法定理を適用すればよい。
$$
\large
\begin{align}
\sin{(3 \alpha)} &= \sin{(2 \alpha+\alpha)} \\
&= \sin{2 \alpha}\cos{\alpha} + \cos{2 \alpha}\sin{\alpha} \\
&= 2 \sin{\alpha}\cos{\alpha} \cdot \cos{\alpha} + (\cos^2{\alpha} – \sin^2{\alpha}) \cdot \sin{\alpha} \\
&= 3\sin{\alpha}\cos^2{\alpha} – \sin^3{\alpha} \\
&= 3\sin{\alpha} – 4\sin^3{\alpha}
\end{align}
$$

$$
\large
\begin{align}
\cos{(3 \alpha)} &= \cos{(2 \alpha+\alpha)} \\
&= \cos{2 \alpha}\cos{\alpha} – \sin{2 \alpha}\sin{\alpha} \\
&= (\cos^2{\alpha}-\sin^2{\alpha}) \cdot \cos{\alpha} – 2 \sin{\alpha}\cos{\alpha} \cdot \sin{\alpha} \\
&= \cos^3{\alpha} – 3\sin^2{\alpha}\cos{\alpha} \\
&= 4\cos^3{\alpha} – \cos{\alpha}
\end{align}
$$

上記の導出にあたっては$\cos^2{\alpha}+\sin^2{\alpha}=1$より、$\cos^2{\alpha}=1-\sin^2{\alpha}, \sin^2{\alpha}=1-\cos^2{\alpha}$を用いた。

極限の公式

公式の概要と導出

$$
\large
\begin{align}
\lim_{\theta \to 0} \frac{\sin{\theta}}{\theta} &= 1 \\
\lim_{\theta \to 0} \frac{1-\cos{\theta}}{\theta^2} &= \frac{1}{2} \\
\lim_{\theta \to 0} \frac{\tan{\theta}}{\theta} &= 1
\end{align}
$$

・$\displaystyle \lim_{\theta \to 0} \frac{\sin{\theta}}{\theta} = 1$の導出
$\theta > 0$で示す。$\theta > 0$では下記が成立する。
$$
\large
\begin{align}
\sin{\theta} < \theta < \tan{\theta}
\end{align}
$$

このとき$\theta > 0$より、$\sin{\theta} > 0$が成立することに基づいて不等式を$\sin{\theta}$で割ると下記が得られる。
$$
\large
\begin{align}
\frac{\cancel{\sin{\theta}}}{\cancel{\sin{\theta}}} < & \frac{\theta}{\sin{\theta}} < \frac{\tan{\theta}}{\sin{\theta}} \\
1 < & \frac{\theta}{\sin{\theta}} < \frac{1}{\cos{\theta}}
\end{align}
$$

ここで$\displaystyle \lim_{\theta \to 0} \frac{1}{\cos{\theta}} = 1$より、下記が成立する。
$$
\large
\begin{align}
\lim_{\theta \to 0} \frac{\theta}{\sin{\theta}} &= 1 \\
\lim_{\theta \to 0} \frac{\sin{\theta}}{\theta} &= 1
\end{align}
$$

・$\displaystyle \lim_{\theta \to 0} \frac{1-\cos{\theta}}{\theta^2} = \frac{1}{2}$の導出
$\displaystyle \lim_{\theta \to 0} \frac{\sin{\theta}}{\theta} = 1$などを用いることで下記のように導出を行うことができる。
$$
\large
\begin{align}
\lim_{\theta \to 0} \frac{1-\cos{\theta}}{\theta^2} &= \lim_{\theta \to 0} \frac{(1-\cos{\theta})(1+\cos{\theta})}{\theta^2(1+\cos{\theta})} \\
&= \lim_{\theta \to 0} \frac{1-\cos^{2}{\theta}}{\theta^2(1+\cos{\theta})} \\
&= \lim_{\theta \to 0} \frac{\sin^{2}{\theta}}{\theta^2(1+\cos{\theta})} \\
&= \lim_{\theta \to 0} \left( \frac{\sin{\theta}}{\theta} \right)^{2} \cdot \frac{1}{1+\cos{\theta}} \\
&= 1 \cdot \frac{1}{1+1} = \frac{1}{2}
\end{align}
$$

・$\displaystyle \lim_{\theta \to 0} \frac{\tan{\theta}}{\theta} = 1$の導出
$\displaystyle \lim_{\theta \to 0} \frac{\sin{\theta}}{\theta} = 1$などを用いることで下記のように導出を行うことができる。
$$
\large
\begin{align}
\lim_{\theta \to 0} \frac{\tan{\theta}}{\theta} &= \lim_{\theta \to 0} \frac{\sin{\theta}}{\theta} \cdot \frac{1}{\cos{\theta}} \\
&= 1 \cdot \frac{1}{1} = 1
\end{align}
$$

上記では高校数学の範囲で式が成立することを示したが、ロピタルの定理を用いるとよりシンプルに示すことができるので合わせて抑えておくと良い。

ロピタルの定理(l’Hopital’s rule)を用いた極限の不定形の計算

Pythonプログラムを用いた数値的・直感的理解

微分の公式

下記で導出を行なった。
https://www.hello-statisticians.com/explain-terms-cat/diff_formula1.html#i-6