分類を行う際の考え方の$1$つに線形識別関数(linear discriminant function)を用いる方法がありますが、法線ベクトルに着目することでシンプルに表すことができます。当記事では法線ベクトルを元に線形識別関数の図形的理解に関して取りまとめました。
作成にあたっては「パターン認識と機械学習」の$4.1$節の「識別関数(Discriminant Functions)」を主に参考にしました。
また、$(\mathrm{o.xx})$の形式の式番号は「パターン認識と機械学習」の式番号に対応させました。
Contents
式の導出
導出目標の確認
$$
\large
\begin{align}
\mathbf{x} = \left( \begin{array}{c} x_{1} \\ \vdots \\ x_{D} \end{array} \right)
\end{align}
$$
上記で表した$D$次元の特徴ベクトル$\mathbf{x} \in \mathbb{R}^{D}$に対して、線形識別関数$y(\mathbf{x})$を下記のように定める。
$$
\large
\begin{align}
y(\mathbf{x}) &= \mathbf{w}^{\mathrm{T}} \mathbf{x} + w_{0} \quad (4.4) \\
\mathbf{w} & \in \mathbb{R}^{D}, \: w_{0} \in \mathbb{R}
\end{align}
$$
このように定めた識別関数$y(\mathbf{x})$は下記のように図式化できる。
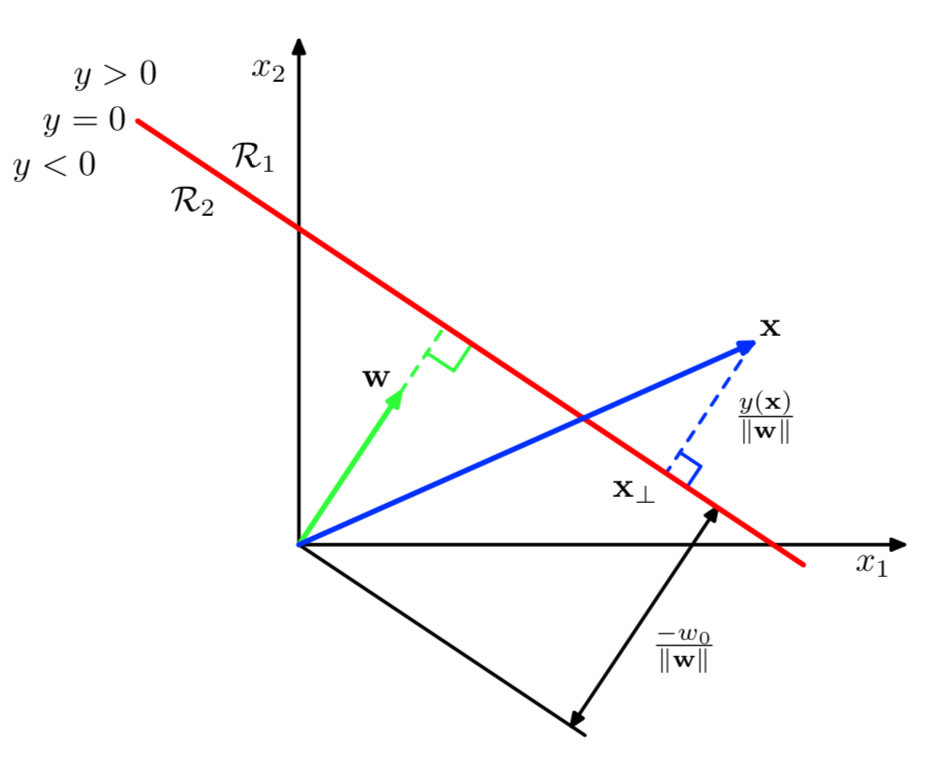
上記の導出を目標に、以下式変形を行う。
原点から$y(\mathbf{x})=0$への距離の計算
$y(\mathbf{x})=0$上の$2$点を$\mathbf{x}_{A},\mathbf{x}_{B}$とおく。このとき、$(4.4)$に基づいて下記が成立する。
$$
\large
\begin{align}
y(\mathbf{x}_{A}) &= \mathbf{w}^{\mathrm{T}} \mathbf{x}_{A} + w_{0} = 0 \quad (1) \\
y(\mathbf{x}_{B}) &= \mathbf{w}^{\mathrm{T}} \mathbf{x}_{B} + w_{0} = 0 \quad (2)
\end{align}
$$
ここで$(1)-(2)$を計算することで、下記が得られる。
$$
\large
\begin{align}
y(\mathbf{x}_{A}) – y(\mathbf{x}_{B}) &= 0 \\
\mathbf{w}^{\mathrm{T}} \mathbf{x}_{A} + \cancel{w_{0}} – (\mathbf{w}^{\mathrm{T}} \mathbf{x}_{B} + \cancel{w_{0}}) &= 0 \\
\mathbf{w}^{\mathrm{T}}(\mathbf{x}_{A}-\mathbf{x}_{B}) &= 0
\end{align}
$$
上記より、パラメータベクトル$\mathbf{w}$は識別関数が構成する平面や直線に垂直であると考えら得れる。よって、原点から$y(\mathbf{x})=0$への距離$d$に関して、下図のように考えることができる。
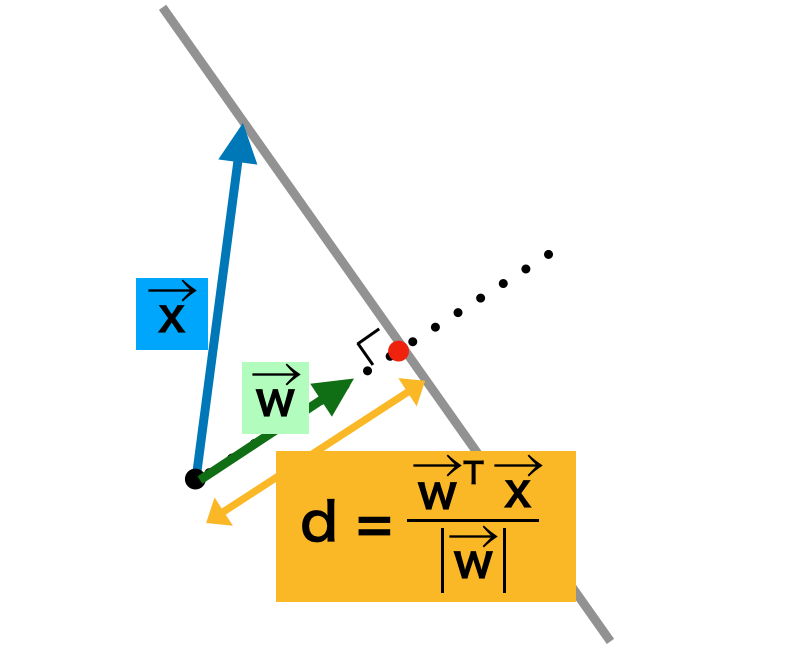
図の作成の都合上、ベクトル$\mathbf{x}$を$\vec{x}$のように表した。上図は「$d$は$\mathbf{x}$と$\mathbf{w}$に平行な単位ベクトルとの内積の絶対値で計算することができる」のように解釈できる。ここでは「パターン認識と機械学習」の$4.1$節の表記に合わせて絶対値を用いなかったが、厳密に考える場合は絶対値をつけると良い。また、$(4.4)$式の$y(\mathbf{x}) = \mathbf{w}^{\mathrm{T}} \mathbf{x} + w_{0}$と$y(\mathbf{x})=0$より、$d$に関して下記も同時に成立する。
$$
\large
\begin{align}
d &= \frac{\mathbf{w}^{\mathrm{T}} \mathbf{x}}{|\mathbf{w}|} \\
&= -\frac{w_0}{|\mathbf{w}|}
\end{align}
$$
$\mathbf{x}$から$y(\mathbf{x})=0$への距離の計算
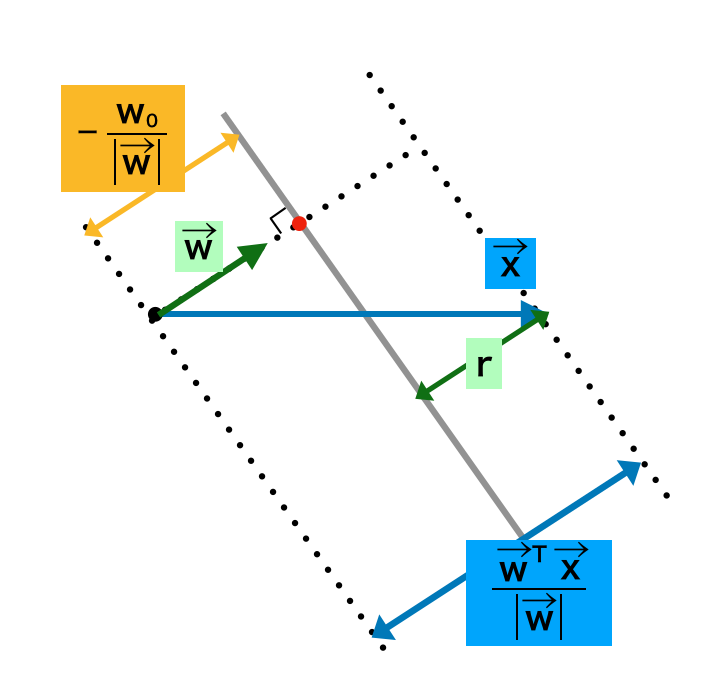
上図のように$r$を考えると、$r$は$\mathbf{x}$から$y(\mathbf{x})=0$への距離に一致する。よって、以下、$r$を計算する。図より、下記の式が成立する。
$$
\large
\begin{align}
\frac{\mathbf{w}^{\mathrm{T}} \mathbf{x}}{|\mathbf{w}|} = -\frac{w_0}{|\mathbf{w}|} + r
\end{align}
$$
上記の両辺に$|\mathbf{w}|$をかけ、$w_0$を加えることで下記のように変形できる。
$$
\large
\begin{align}
\frac{\mathbf{w}^{\mathrm{T}} \mathbf{x}}{|\mathbf{w}|} &= -\frac{w_0}{|\mathbf{w}|} + r \\
\mathbf{w}^{\mathrm{T}} \mathbf{x} &= -w_0 + r |\mathbf{w}| \\
\mathbf{w}^{\mathrm{T}} \mathbf{x} + w_0 &= r |\mathbf{w}| \\
y(\mathbf{x}) &= r |\mathbf{w}| \\
r &= \frac{y(\mathbf{x})}{|\mathbf{w}|}
\end{align}
$$
