$2$変数関数の描画を手動で行う場合はなかなか難しいのでPythonのようなプログラム言語を用いる描画法を抑えておくと様々な所で役に立ちます。当記事ではnumpy.meshgridとmatplotlib.pyplotのいくつかのメソッドを用いた2変数関数の描画について取り扱いました。
・Pythonまとめ
https://www.hello-statisticians.com/python_basic
np.meshgridを用いた格子点の作成
NumPyのmeshgridメソッドは下記のように実行することができます。
import numpy as np
x_, y_ = np.arange(-2,2.01,0.01), np.arange(-2,2.01,0.01)
x, y = np.meshgrid(x_, y_)
print(x)
print("===")
print(y)・実行結果
[[-2. -1.99 -1.98 ... 1.98 1.99 2. ]
[-2. -1.99 -1.98 ... 1.98 1.99 2. ]
[-2. -1.99 -1.98 ... 1.98 1.99 2. ]
...
[-2. -1.99 -1.98 ... 1.98 1.99 2. ]
[-2. -1.99 -1.98 ... 1.98 1.99 2. ]
[-2. -1.99 -1.98 ... 1.98 1.99 2. ]]
===
[[-2. -2. -2. ... -2. -2. -2. ]
[-1.99 -1.99 -1.99 ... -1.99 -1.99 -1.99]
[-1.98 -1.98 -1.98 ... -1.98 -1.98 -1.98]
...
[ 1.98 1.98 1.98 ... 1.98 1.98 1.98]
[ 1.99 1.99 1.99 ... 1.99 1.99 1.99]
[ 2. 2. 2. ... 2. 2. 2. ]]計算結果より$-2 \leq x \leq 2, \, -2 \leq y \leq 2$の領域の点を$0.01$刻みで表されたことが確認できます。数学ではそれぞれの点に$(x,y)$の$2$つの値を対応させて表すことが多いですが、np.meshgridではそれぞれの点における$x$と$y$の値を分けて表すことに注意が必要です。
matplotlib.pyplotを用いた描画
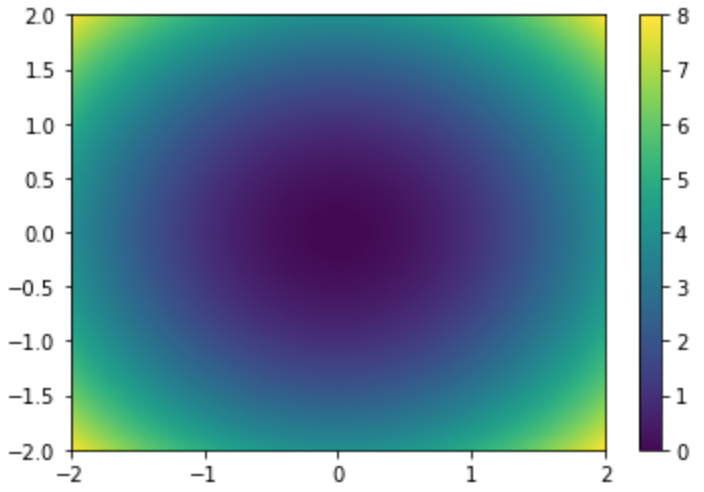
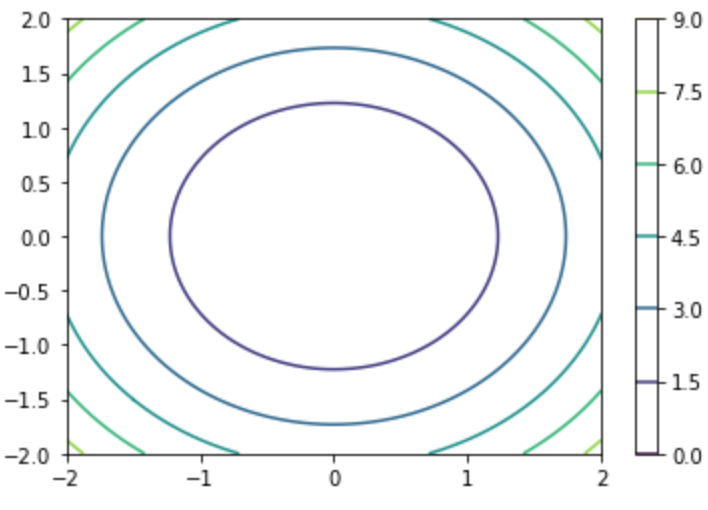
以下では$2$変数関数$f(x,y) = x^2 + y^2$の描画を行います。
plt.contour
pyplot.contourを下記のように用いることで$2$変数関数の等高線の描画を行うことができます。
import numpy as np
import matplotlib.pyplot as plt
x_, y_ = np.arange(-2,2.01,0.01), np.arange(-2,2.01,0.01)
x, y = np.meshgrid(x_, y_)
z = x**2 + y**2
plt.contour(x,y,z,cmap="viridis")
plt.colorbar()
plt.show()・実行結果
plt.pcolormesh
pyplot.pcolormeshを下記のように用いることで$2$変数関数のカラーマップの描画を行うことができます。
import numpy as np
import matplotlib.pyplot as plt
x_, y_ = np.arange(-2,2.01,0.01), np.arange(-2,2.01,0.01)
x, y = np.meshgrid(x_, y_)
z = x**2 + y**2
plt.pcolormesh(x,y,z,cmap="viridis")
plt.colorbar()
plt.show()・実行結果